Минимизация ДНФ. Тупикова ДНФ

Даже если ДНФ сокращенная, ее можно минимизировать, то есть уменьшить количество входящих в нее элементарных конъюнкций.

Пример. Пусть сокращенная ДНФ функции имеет вид:

.

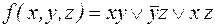Тогда ее единичное множество может быть представлено в виде:

.

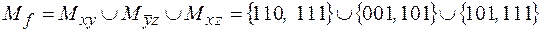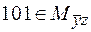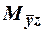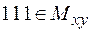Заметим, что наборы, входящие в последнее подмножество, находятся так же в первом и во втором. Так ( говорят, набор 101 покрывается множеством ), а . Значит, если убрать из объединения составляющую 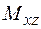, объединение от этого не изменится. Говорят, что множество 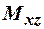покрывается объединением 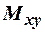и 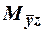. Следовательно, импликант xz – лишний.

Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой.

 

Отношение покрытия между единичными наборами и импликантами ДНФ наглядно задается таблицей покрытия.

Строки таблицы соответствуют конъюнкциям ДНФ, столбцы – элементам единичного множества. На пересечении строки и столбца ставится пометка, если данная конъюнкция обращается в единицу данным набором значений аргументов (иначе говоря, данный набор покрывается единичным множеством конъюнкции).

Пример. Пусть ДНФ функции имеет вид:

.

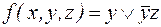Тогда ее единичное множество может быть представлено в виде:

.

.

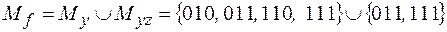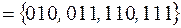Построим таблицу покрытия.

 

y

 

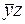
Из таблицы видно, что вторая строчка – лишняя, то есть если ее убрать, все элементы единичного множества останутся покрыты. Значит, импликант 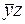– лишний. Таким образом, ДНФ можно упростить, убрав лишний импликант. Она приобретает вид 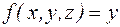, и в данном случае является тупиковой, так как оставшийся импликант – простой.

Так бывает не всегда.

Замечание.1 Чтобы с помощью таблицы покрытия получить тупиковую ДНФ, необходимо сначала получить сокращенную ДНФ и именно ее простые импликанты помещать в таблицу покрытия.

Замечание.2 У функции может быть несколько тупиковых ДНФ. Чтобы найти их необходимо построить сокращенную ДНФ, содержащую все простые импликанты данной функции.

Метод Блейка-Порецкого – метод получения сокращенной ДНФ, содержащей все простые импликанты.

Пусть дана СДНФ функции.

1. Перенумеруем элементарные конъюнкции.

2. Осуществим попарно склеивание каждой конъюнкции с каждой, если это возможно. Под полученными конъюнкциями будем фиксировать номера.

3. Допишем к списку полученных конъюнкций те, которые не участвовали в склеивании (их номера не фиксировались).

4. Вернемся к п.1.

В результате получим сокращенную ДНФ, содержащую все простые импликанты.

Пример. Дана СДНФ вида:

.

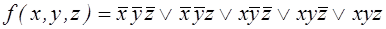Получить с помощью метода Блейка-Порецкого сокращенную ДНФ, содержащую все простые импликанты.

 

П. 1. ;

П. 2, 3. ;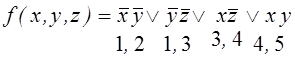

П.4. .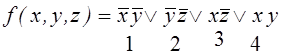

Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: .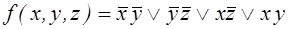

Построим таблицу покрытия:

 

 

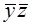
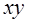
Из таблицы видно, что первую строку удалять нельзя, так как при этом останется не покрыт набор 001. Вторую строку можно удалить, так как наборы, составляющие единичное множество конъюнкции 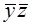, содержаться также в единичных множествах других конъюнкций. Аналогично с третьей строкой. Последнюю строку также нельзя удалить, так как если это сделать, останется не покрыт набор 111.

Таким образом, дана функция имеет 2 тупиковые ДНФ:

;

.

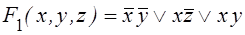Пример 2.

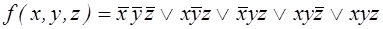
П. 1. ;

П. 2, 3. ;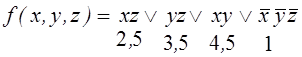

П.4. ;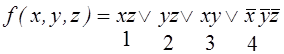

Так как больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: .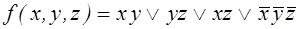

Построим таблицу покрытия:

 

 

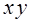
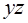
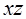
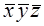
Из таблицы видно, что при удалении любой ее строки появятся единичные наборы, не покрытые никаким единичным множеством. Следовательно, полученная сокращенная ДНФ является тупиковой.

 

Алгебра Жегалкина

Алгеброй Жегалкина называется алгебра вида 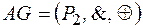. В алгебре Жегалкина действуют тождества:

1) коммутативность сложения по модулю 2

;

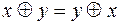2) ассоциативность сложения по модулю 2

;

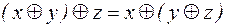3) дистрибутивность конъюнкции по отношению к сложению по модулю 2

,

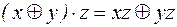4)

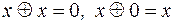
а также все тождества, истинные для конъюнкции.

От любой булевой формулы можно перейти к формуле алгебры Жегалкина, используя тождества:

,

.

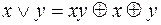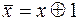Полином Жегалкина – это формула алгебры Жегалкина, имеющая вид суммы по модулю 2 элементарных конъюнкций различного количества переменных без отрицаний.

Линейной функцией называется функция, полином Жегалкина которой имеет вид:

,

где, .

Двойственность

Функция 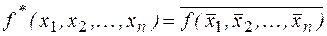называется двойственнойфункцией к функции .

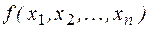Чтобы получить двойственную функцию из исходной, надо каждой переменной придать отрицание на самом нижнем уровне формулы, затем общее отрицание всей формуле (на самом верхнем уровне) и привести к ДНФ (упростить).

У двойственной функции на противоположных наборах принимаются противоположные значения: если , то .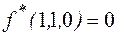

Функция 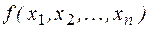называется самодвойственной,если .

Самодвойственными являются функции .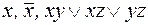

Вектор-столбец самодвойственной функции антисимметричен относительно своей середины (при лексикографическом порядке аргументов).