Комбинационные схемы

Комбинационные элементы – электронные компоненты, техническая реализация которых может быть основана на использовании различных физических явлений: магнитных, явлений в полупроводниках и т. д. Они являются основными компонентами компьютеров.

Все комбинационные элементы имеют один или более входов и один выход. Каждый вход может принимать одно из двух значений (обычно низкое или высокое напряжение).

Наиболее важные типы комбинационных элементов приведены в таблице 1.

Различные комбинационные элементы могут быть связаны друг с другом в цепи так, что выход одних является входом других.

Таблица 1

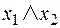
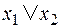
Элементы	Конъюнкция	Дизъюнкция	Отрицание
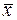
Обозначения

Такие цепи называются комбинационными схемами (логическими сетями).

Так как штрих Шеффера и стрелка Пирса являются функционально полными системами, возможно описание выходов комбинационных схем с помощью каждого из этих элементов.

Пример.

Построить комбинационную схему в базисе «штрих Шеффера», реализующую дизъюнкцию .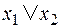

Так как 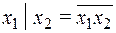. А отрицание 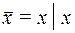, то дизъюнкция

.

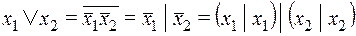Обозначим комбинационный элемент, соответствующий функции «штрих Шеффера» обозначим в виде:

Тогда соответствующая схема приобретает вид:

Очевидно, данная схем более сложная, чем та, что могла быть построена в базисе .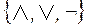

Литература

1. Виленкин, Н. Я. Комбинаторика. – М.: Наука, 1969. – 328 с.

2. Гаврилов, Г. П. Задачи и упражнения по курсу дискретной математики: учеб. пособие / Г. П. Гаврилов, А. А. Сапоженко. – М.: Наука, 1992. – 408 с.

3. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979.– 400 с., ил.

4. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. для вузов. – 12-е изд., перераб. – М.: Высшее образование, 2008. – 479 с.: граф., табл.

5. Гутова, С. Г. Теория вероятностей и математическая статистика: учеб.-метод. пособие/ ГОУ ВПО «Кемеровский государственный университет»; сост. С. Г. Гутова. – Кемерово: ИНТ, 2008. – 108 с.

6. Кузнецов, О. П. Дискретная математика для инженера/ О. П. Кузнецов, Г. М. Адельсон-Вельский. – М.: Энергоатомиздат, 1986. – 480 с.

7. Кук, Д. Компьютерная математика: пер. с англ./ Д. Кук, Г. Бейз. – М.: Наука, Гл. ред. физ.-мат. лит., 1990. – 384 с.

8. Чуешева, О. А. Математическая логика: учеб.-метод. пособие/ сост. О. А. Чуешева. – Кемерово, 2006. – 48 с.

9. Щекочихина, С. Г. Дискретная математика: вопросы для самостоятельного изучения для студентов 1 курса МФ спец. 01.02. – Кемерово: Кузбассвузиздат, 2003. – 64 с.

10. Яблонский, С. В. Введение в дискретную математику: учеб. пособие. – М.: Наука, 1986. – 384 с.