Принцип двойственности

Если в формуле F, представляющей функцию f все знаки функций заменить на знаки двойственных функций, то получится формула 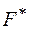, представляющая функцию 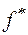, двойственную к f.

Пример. Получить функцию, двойственную к 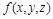с помощью определения двойственной функции. Выяснить, является ли функция самодвойственной.

.

.

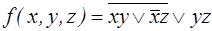
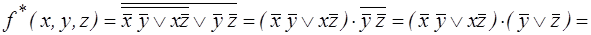
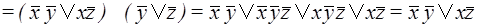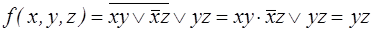Вывод: функция не самодвойственна.

Функциональная полнота систем

Функционально полной называется такая система функций 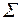, через функции которой можно выразить любую логическую функцию.

Например, 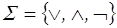. Эта система функционально полна, так как любая функция имеет булеву формулу.

Теорема.

Произвольная система 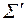будет функционально полной, если она сводится к функционально полной системе .

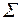Это означает, что через функции системы 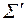можно выразить все функции системы .

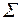Лемма 1.

Если функция 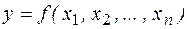– немонотонна, то подстановкой n-1 константы из нее можно получить отрицание.

Лемма 2.

Если функция 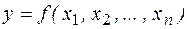– нелинейна, то подстановкой n-2 констант из нее можно получить дизъюнкцию и конъюнкцию.

Функционально полной в слабом смысле называется такая система функций 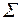, которая становится функционально полной, если к ней добавить константы 0 и 1.

Например, 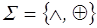– функционально полна в слабом смысле. Эта система функций алгебры Жегалкина. Для того, чтоб с ее помощью можно было записать все полиномы Жегалкина, необходимо добавить константу 1. Это означает, что 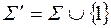– функционально полна (в сильном смысле).