Минимизация логических функций
Одна и та же функция может иметь несколько аналитических представлений. Функция называется минимальной, если ее аналитическое представление имеет минимальное количество слагаемых и минимальное количество переменных в каждом слагаемом. Таким образом, минимизация справедлива только для аналитического представления логической функции в виде ДНФ.
Существует несколько методов минимизации логических функций. Наиболее простым и эффективным является метод Блейка.
Правило 6.6. (метод Блейка) Алгоритм метода состоит из трех этапов:
1) привести формулу к ДНФ;
2) для всевозможных пар слагаемых, если это возможно, применить операцию склеивания:
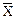 Y + XZ =
Y + XZ = 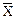 Y + XZ + YZ;
Y + XZ + YZ;
3) к исходным и полученным слагаемым применить операцию поглощения:
X + XY = X.
Пример 6.6. Минимизировать функцию из примера 6.2.
Решение. Исходная функция имеет вид:
f(X, Y, Z) = 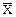 YZ + XY
YZ + XY 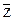 + XYZ.
+ XYZ.
Выполним последовательно этапы метода Блейка. Применим операцию склеивания для всевозможных пар слагаемых:
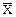 YZ + XY
YZ + XY 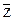 =
= 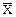 YZ + XY
YZ + XY 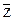 + YZY
+ YZY 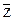 =
= 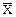 YZ + XY
YZ + XY 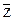 + 0;
+ 0;
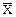 YZ + XYZ =
YZ + XYZ = 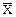 YZ + XYZ + YZ;
YZ + XYZ + YZ;
YZ + XY 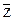 = YZ + XY
= YZ + XY 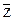 + XY;
+ XY;
XY + 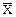 YZ = XY +
YZ = XY + 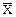 YZ + YZ.
YZ + YZ.
В результате выполнения второго этапа получено следующее выражение:
f(X, Y, Z) = 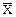 YZ + XY
YZ + XY 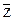 + XYZ + YZ + XY.
+ XYZ + YZ + XY.
Применим операцию поглощения:
f(X, Y, Z) = YZ + XY.
Таким образом, функция минимизирована. Сравните полученный результат с упрощением функции в примере 6.5, то есть минимизация может быть достигнута преобразованиями над функцией. □
Дата добавления: 2019-04-03; просмотров: 625;
