Модели представления знаний
Представление знаний происходит в рамках той или иной системы представления знаний. Система представления знаний – это совокупность программных средств для хранения и обработки знаний. Система представления знаний выполняет следующие функции:
- хранение знаний о предметной области в соответствии с моделью представления знаний в базе знаний (БЗ);
- ввод новых знаний;
- проверка непротиворечивости хранимых знаний;
- удаление знаний;
- вывод новых знаний из уже имеющихся знаний;
- предоставление знаний пользователю.
Модель представления знаний – это способ записи знаний, предназначенный для отображения текущего состояния объектов некоторой предметной области и отношений между ними, а также изменение объектов и отношений.
Модель представления знаний может быть универсальной, то есть применимой для большинства предметных областей, или специализированной, то есть разработанной для конкретной предметной области. К основным универсальным моделям представления знаний относятся:
- логические модели;
- сетевые модели;
- продукционные модели;
- фреймовые модели.
Знания хранятся в базе знаний в соответствии с моделью представления знаний.
Логические модели
В основе логических моделей лежит понятие формальной теории, задаваемой четверкой:
S = < T, F, A, R >.
Рассмотрим компоненты формальной теории.
T – множество символов теории S, называемых термами и образующих алфавит теории. Конечная последовательность символов множества T называется выражением теории S.
F – подмножество выражений теории S, называемых формулами теории и построенных по синтаксическим правилам. Примерами правил могут быть праивла записи формул алгебры высказываний.
A – множество формул, называемых аксиомами теории S и являющихся априорно истинными формулами.
R – конечное множество отношений между формулами, называемые правилами вывода. Правила вывода позволяют получать новые формулы множества F за счет применения этих правил вывода к аксиомам или уже выведенным формулам.
Формальная система позволяет выводить новые правильные формулы множества F, применяя к аксиомам множества A и уже полученным формулам правила вывода множества R, то есть выводить из одних истинных высказываний новые истинные высказывания. Таким образом, в рамках формальной системы можно получить бесконечное число формул из небольшого числа исходных аксиом.
Вывод новых знаний в рамках логической модели представления знаний заключается в получении некоторого утверждения из имеющихся аксиом и правил вывод. Если в результате вывода утверждение получено, то оно считается истинным и является логическим следствием из аксиом.
В этом случае задачей пользователя или программиста является описание предметной области совокупностью утверждений в виде логических формул. Доказательство истинности утверждения осуществляется ЭВМ на основе исходных утверждений.
Наиболее простой метод логического вывода использует только одно правило вывода и называется методом резолюции.
Метод резолюции заключается в выполнении следующих шагов:
1) взять отрицание формулы A и привести формулу 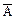 к КНФ;
к КНФ;
2) выписать множество дизъюнктов K = {D1, ..., Dn} формулы 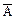 ;
;
3) если во множестве существуют пара дизъюнктов Di и Dj, один из которых содержит переменную Y, а другой – отрицание переменной 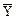 , то соединить эти дизъюнкты дизъюнкции Di + Dj и сформировать новый дизъюнкт
, то соединить эти дизъюнкты дизъюнкции Di + Dj и сформировать новый дизъюнкт 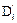 +
+ 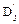 , исключив переменные Y и
, исключив переменные Y и 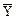 ;
;
4) возможны три случая:
- если дизъюнкты Di и Dj содержат только переменные Y и 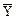 , то получен пустой дизъюнкт и логическое следствие верно;
, то получен пустой дизъюнкт и логическое следствие верно;
- если во множестве K не существует двух дизъюнктов, для которых применим шаг 3, то логическое следствие неверно;
- если полученный дизъюнкт не является пустым, то и добавить его к множеству K и вновь выполнить шаг 3.
Пример 7.1. Рассмотрим логический вывод знаний. Пусть для некоторого студента справедливы три факта, являющихся аксиомами – исходными утверждениями для логического вывода:
1) если студент болеет, то он принимает лекарства;
2) если студент не болеет, то он ходит на учебу;
3) студент не принимает лекарства.
Следует ли из этих аксиом следующее высказывание:
4) студент ходит на учебу.
Выделим в этих утверждениях простые высказывания:
A = «студент болеет»;
B = «студент принимает лекарства»;
C = «студент ходит на учебу».
Запишем утверждения с помощью этих простых высказываний с учетом того, что конструкция «если A, то B» соответствует логической операции импликации A → B:
1) A → B;
2) 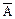 → C;
→ C;
3) 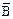 ;
;
4) C.
При преобразованиях будем использовать следующие равносильные формулы алгебры высказываний:
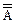 = A;
= A;
A → B = 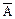 + B;
+ B;
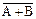 =
= 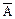 ×
× 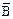 ,
,
где «+» – дизъюнкция; «×» – операция конъюнкции; «→» – операция логического следствия (импликация).
Проверим, является ли высказывание 4 логическим выводом из утверждений 1-3:
[(A → B) × ( 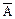 → C) ×
→ C) × 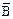 ] → C.
] → C.
В соответствии с методом резолюций возьмем отрицание от данного выражения и преобразуем его к КНФ:
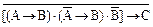 = (
= ( 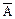 + B) × (A + C) ×
+ B) × (A + C) × 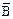 ×
× 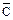 .
.
Множество K включает следующие дизъюнкты:
K = { 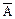 + B, A + C,
+ B, A + C, 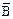 ,
, 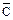 }.
}.
Из двух дизъюнктов 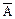 + B и A + C получим новый дизъюнкт B + C, который включается в множество K:
+ B и A + C получим новый дизъюнкт B + C, который включается в множество K:
K = { 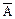 + B, A + C,
+ B, A + C, 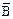 ,
, 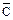 , B + C}.
, B + C}.
Из двух дизъюнктов B + C и 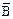 получим новый дизъюнкт C, который также включается во множество K:
получим новый дизъюнкт C, который также включается во множество K:
K = { 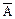 + B, A + C,
+ B, A + C, 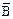 ,
, 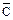 , B + C, C}.
, B + C, C}.
Полученный дизъюнкт C является отрицанием дизъюнкта 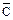 , а значит, высказывание 4 является логическим следствием из утверждений 1-3. □
, а значит, высказывание 4 является логическим следствием из утверждений 1-3. □
Помимо высказываний, для представления знаний могут использоваться предикаты. В отличие от естественного языка, который очень сложен, язык логики предикатов использует конструкции естественного языка, которые легко формализуются.
Предикат – это функция, возвращающая значения 1 («истина») или 0 («ложь») в зависимости от значений аргументов. Например, P(x,y)=(x>y).
В логике предикатов вводятся две операции.
1. Квантор существования $.
Выражение $x P(x) (читается: «существует x, для которого P(x)») истинно, если существует такое значение x из множества M, при котором P(x) = 1:
$x P(x) = P(x1) + P(x2) + …
2. Квантор общности ".
Выражение "x P(x) («для любого x P(x)») истинно, если P(x) = 1 для всех значений x из множества M:
"x P(x) = P(x1) · P(x2) · …
Рассмотрим пример представления знаний с помощью предикатов.
Пример 7.2. Приведем структуру описания следующего объекта с помощью логики предикатов: «Солнечная система состоит из центрального светила и девяти планет, обращающихся вокруг него».
Выражения «состоит из» и «представляет собой» используют для того, чтобы описать структуру некоторого объекта. Описание может быть статическим и динамическим.
В случае статического описания указывается взаимное пространственное расположение частей. В случае динамического описания – законы их относительного перемещения в пространстве или описание иных видов движения (их зависимости от времени).
Для нашего примера, считая для простоты, что планеты равномерно движутся по круговым орбитам, можно построить следующее описание, используя следующее выражение:
"x $y "t (СОЛНЕЧНАЯ_СИСТЕМА (х, t) º
º СОСТОИТ_ИЗ(x, y, t) ×
× $z0 $z1 … $z8 "z (((z Î y) ® ((z = z0) + (z = z1) + … + (z = z8)) ×
× СОЛНЦЕ(z0) × МЕРКУРИЙ(z1) × ВЕНЕРА(z2) ×
ЗЕМЛЯ(z3) × МАРС(z4) × ЮПИТЕР(z5) × САТУРН(z6) ×
× УРАН(z7) × НЕПТУН(z8) ×
× $ 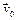 КООРДИНАТЫ(z0, t,
КООРДИНАТЫ(z0, t, 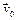 ) × (
) × ( 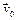 = 0)) ×
= 0)) ×
× 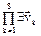 (КООРДИНАТЫ (zk, t,
(КООРДИНАТЫ (zk, t, 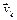 ) ×
) ×
× (rk = ak) × (qk = bk) × (jk = ck Å dk Ä t)))),
где º – логическая операция эквивалентности, «Å» – операция арифметического сложения; «Ä» – операция арифметического умножения; t – время.
Для описания пространственного положения космических тел определяются: 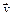 – координатный вектор в сферической системе координат
– координатный вектор в сферической системе координат 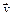 = < r, q, j> (соответственно,
= < r, q, j> (соответственно, 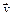 = 0 следует понимать как (r = 0) × (q = 0) × (j = 0), а $
= 0 следует понимать как (r = 0) × (q = 0) × (j = 0), а $ 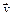 как кортеж из трех кванторов); ak, bk, ck, dk – числа, определяющие соответственно радиус орбиты, угол наклона орбиты, положение на орбите, период обращения.
как кортеж из трех кванторов); ak, bk, ck, dk – числа, определяющие соответственно радиус орбиты, угол наклона орбиты, положение на орбите, период обращения.
Названия Солнца и девяти планет символизируют не только имя, но и все существенные характеристики соответствующего объекта. Например:
МАРС(z4) º (ИМЯ (z4, МАРС) × МАССА(z4; 6,4Ä1013) ×
× ПЕРИОД_ВРАЩЕНИЯ_ВОКРУГ_СВОЕЙ_ОСИ(z4; 24,5) ×
× СРЕДНИЙ_ДИАМЕТР(z4, 6776)).
Общий вид такого описания можно представить схемой
"x $y "t (А(x, t) ~ СОСТОИТ_ИЗ(x, y, t) × S(y, t)),
где S(y, t) – описание совокупности y как статической или динамической системы пространственно организованных элементов. □
Возможность получения новых знаний из уже имеющихся знаний (аксиом) посредством логического вывода делает логические модели представления знаний широко используемыми в системах искусственного интеллекта.
Семантические сети
Семантическая сеть – это система знаний, имеющая вид сети, узлы которой соответствуют объектам предметной области и их свойствам, а дуги – отношениям между ними.
Представим с помощью семантической сети следующие факты:
«все кашалоты – киты»,
«Моби Дик – кашалот»,
«киты имеют хвост».
Моби Дику посвящен одноименный роман американского писателя Германа Мелвилла.
Из данных фактов можно выделить следующие объекты, которые будут являться узлами сети: «Моби Дик», «кашалот», «кит», «хвост».
Взаимосвязь этих объектов опишем с помощью отношений:
- «часть – целое» (IS-A) (пример: «стол» IS-A «мебель»);
- «целое – частное» (PART-OF) (пример: «рука» PART-OF «тело»).
Семантическая сеть, описывающая факты, представлена на рис. 7.1.

Рис. 7.1. Представление фактов семантической сетью
Используя отношения IS-A и PART-OF, из имеющихся фактов можно вывести факты «Моби Дик – кит» и «Моби Дик имеет хвост».
Семантическая сеть представляет собой ориентированный граф с поименованными дугами и вершинами. Вершинам графа, описывающего семантическую сеть, соответствуют:
- события представляют собой действия, происходящие в реальном мире;
- объекты представляют объекты реального мира, а также их особенности и характеристики (цвет, размер, качество), а применительно к событиям – продолжительность, время, место.
Дуги графа семантической сети отображают многообразие отношений между объектами, которые условно можно разделить на четыре класса:
- лингвистические отношения в свою очередь подразделяются на глагольные (время, вид, род, залог, наклонение), атрибутивные (цвет, размер, форма) и падежные;
- логические отношения, используемые в алгебре высказываний: дизъюнкция, конъюнкция, отрицание, импликация и др.;
- теоретико-множественные: отношение части целого (PART-OF), отношение множества и элемента (IS-A);
- квантифицированные отношения общности и существования; они используются для представления таких утверждений как «Любой станок надо ремонтировать», «Существует работник А, обслуживающий склад Б».
Рассмотренный выше пример семантической сети отображал теоретико-множественные отношения между объектами, представляющие понятия предметной области. Рассмотрим использование семантических сетей для представления событий.
Чтобы представить некоторые знания о событиях в виде семантической сети, необходимо выделить данные события. События обычно описываются глаголом. После этого выделяются следующие объекты:
- объекты, которые являются инициаторами события;
- объекты, на которые событие воздействует;
- объекты, характеризующие свойства события.
Все связи понятий, событий и свойств с действием (глаголом) называют падежами или падежными отношениями, которые относятся к классу лингвистических отношений (табл. 7.2).
Таблица 7.2. Возможные падежи
| Падеж | Значение падежа |
| агент | предмет, являющийся инициатором действия |
| объект | предмет, подвергающийся действию |
| источник | размещение предмета перед действием |
| приемник | размещение предмета после действия |
| время | момент выполнения действия |
| место | место проведения действия |
| цель | действие другого события |
Введение падежей позволяет перейти от поверхностной структуры к его смысловому содержанию.
Представим в виде семантической сети предложение: «Студент пришел в 18.50 с работы в университет на занятие, чтобы сдать лабораторную работу в компьютерном классе».
Выделим основные события в этом предложении, соответствующие действиям:
F1 – студент пришел;
F2 – пришел, чтобы сдать.
Схема семантической сети представлена на рис. 7.2.
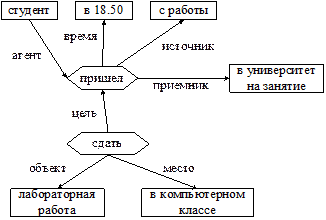
Рис. 7.2. Представление знаний семантической сетью
Особенность семантических сетей как модели представления знаний состоит в единстве БЗ и механизма вывода новых знаний.
Рассмотрим метод сопоставления, который заключается в выполнении следующих шагов:
1) строится семантическая сеть, соответствующая структуре запроса;
2) сеть запроса сопоставляется с семантической сетью, в результате чего отыскивается искомый узел, который и является ответом.
Запрос «Куда пришел студент?» представим в виде сети (рис. 7.3).
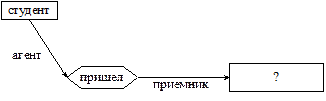
Рис. 7.3. Семантическая сеть запроса «Куда пришел студент?»
Сопоставление общей сети с сетью запроса начинается с поиска вершины «пришел», имеющей дугу «агент», направленную от вершины «студент». Затем происходит переход по дуге «приемник», что приводит к ответу «в университет на занятие».
Наряду с методом сопоставления, в семантических сетях используется метод перекрестного поиска, состоящий из двух шагов:
1) поиск отношений между понятиями;
2) вершина, находящаяся на пересечении дуг, соответствующих отношениям в запросе, является ответом на запрос.
Сеть запроса «Что сделал студент в 18.50?» представлена на рис. 7.4.
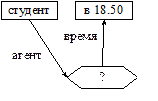
Рис. 7.4. Семантическая сеть запроса
«Что сделал студент в 18.50?»
Сопоставление общей сети с сетью запроса начинается с поиска вершины, в которую сходятся дуги «агент» и «объект». В данной семантической сети присутствует одна вершина «пришел», и она связана падежами с вершинами «студент» и «в 18.50». Поэтому вершина «пришел» является ответом на этот запрос.
Любую семантическую сеть можно записать с помощью предикатов, то есть преобразовать семантические сети к логической модели представления знаний. Например, семантическую сеть, изображенную на рис. 7.1, можно описать с помощью предикатов
является (элемент, множество);
имеет (часть, объект),
следующим образом:
является (кашалот, кит);
является (Моби Дик, кашалот);
имеет (хвост, кит).
Отношение «студент – пришел» на рис. 7.2 можно описать предикатом
агент (инициатор, действие).
Другие отношения между объектами можно описать аналогичными предикатами.
Семантические сети, как модель представления знаний, имеют следующие преимущества:
- описание объектов и событий производится на уровне близком к естественному языку;
- возможность объединение нескольких семантических сетей в одну;
- возможность выделения фрагмента сети и использования ее в качестве автономной БЗ, содержащей все необходимые объекты, события и отношения между ними;
- небольшое число типов отношений между объектами и событиями.
Дата добавления: 2019-04-03; просмотров: 3146;
