Особенности описания микрочастиц

Корпускулярно-волновой дуализм свойств материи.

Одной из наиболее спорных проблем в истории естествознания была проблема природы лучистой энергии – электромагнитного излучения. Взгляды физиков на природу света (волна или поток частиц), начиная с Исаака Ньютона (Newton), периодически менялись. К концу XIX века общепринятым считалось, что электромагнитное излучение имеет волновую природу. Однако к началу XX века встала проблема описания явления излучения света нагретыми телами. Не удавалось создать на основе классической электродинамики модель, объясняющую излучательную способность нагретых тел. Макс Планк (Planck) предложил гипотезу о квантовой природе процесса излучения (1900), согласно которой излучение энергии нагретым абсолютно черным телом происходит не непрерывно, как того требовала классическая теория, а дискретными порциями – квантами. Минимальная энергия – величина энергии кванта – пропорциональна частоте излучения:

E = h×n,

где h = 6,6262×10^-34 Дж×с – постоянная Планка, n – частота излучения, с^-1.

Альберт Эйнштейн (Einstein) высказал предположение о том, что идея квантования энергии относится не только к процессам поглощения и испускания света нагретыми телами, но и к излучению как таковому. То есть электромагнитное излучение распространяется в виде дискретных частиц с энергией E = hn, названых впоследствии фотонами. Такие радикальные изменения во взглядах на природу света, предложенные Планком и Эйнштейном, нашли экспериментальное подтверждение в исследовании фотоэффекта – испускания электронов веществом под действием света. И особенно корпускулярные свойства электромагнитного излучения проявились в рассеянии рентгеновского излучения различными веществами – эффект Комптона, все особенности которого можно объяснить упругим столкновением фотонов рентгеновского излучения со слабосвязанными электронами.

Таким образом, поток электромагнитного излучения, с одной стороны, является волной, что наблюдается при интерференции и дифракции, а с другой стороны, – потоком частиц, что экспериментально проявляется в процессах испускания, поглощения и рассеяния излучения твердыми телами.

Используя выражение Планка для энергии кванта излучения и формулу Эйнштейна, показывающую взаимосвязь энергии частицы и ее массы (E = mc²), можно связать характеристики фотона (масса, импульс) и характеристики волны (длина волны и частота):

E = hn E = mc² ® hn = mc²

n = c/l ® hc/l = mc² ® m = h/cl ® l = h/mc

p = m×c ® ;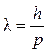

h – постоянная Планка; n – частота излучения; m – масса фотона, кг; c– скорость света в вакууме; l – длина волны излучения, м; p – импульс фотона.

Так все же фотон – волна или частица? Скорее всего, сущность этой проблемы связана с ограниченностью наших жизненных представлений. Мы живем в макромире, где только по отдельности встречаются процессы, имеющие корпускулярную и волновую природу. Нигде в повседневной жизни мы не встречаемся с движением, которое было бы результатом наложения этих двух форм, но это не значит, что его не существует. Из этой дилеммы возник совершенно новый подход к описанию физических и химических процессов микромира.

В 1924 г. Луи де Бройль (de Broglie) выдвинул гипотезу о том, что корпускулярно-волновой дуализм свойственен не только электромагнитному излучению, а является общим свойством материи. При этом он ввел понятие о волнах материи. Так, любому материальному объекту, обладающему массой m и движущемуся со скоростью v, соответствует волновой процесс с длиной волны l. По аналогии с электромагнитным излучением, где l=h/p, длина волны частицы (часто называется длиной волны де Бройля) вычисляется по уравнению

.

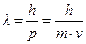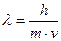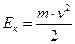Так, электроны, испускаемые нагретым катодом, разгоняются в электрическом поле напряжением » 100 В, приобретают кинетическую энергию »100 эВ. При этом в случае, если формула де Бройля верна, электронам должна соответствовать длина волны .Если , то 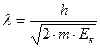. При E_к = 100 эВ,l = 1,2 Å.

Если электроны обладают волновыми свойствами, то их пучок должен испытывать дифракцию на дифракционной решетке, постоянная которой a соизмерима с длиной волны электрона (постоянная решетки − сумма ширины щели и ширины промежутка между щелями). Так как длина волны электрона мала (l=1.2 Å), то роль дифракционной решетки, у которой a » l, могут играть кристаллические плоскости монокристаллов. В частности, была использована металлическая фольга (никель). Причем положение дифракционных полос должно определяться условием Уильяма Брэгга (Bragg): n×l = 2×a×sinJ (n − номер дифракционной полосы; J − угол, под которым пучок электронов попадает на дифракционную решетку).

Экспериментальное подтверждение волновых свойств электрона было получено в 1927 г. Клинтоном Девиссоном (Devisson) и Лестером Джермером (Gemmer) и независимо от них Джоржем Томсоном (Thomson) (1928 г.) в опытах по рассеянию электронов. Действительно, при пропускании пучка электронов через металлическую фольгу была получена дифракционная картина в виде концентрических колец, положение которых изменялось в зависимости от кинетической энергии электронов (ускоряющего напряжения) – их длины волны, согласно условию Брэгга (рис. 2.2).

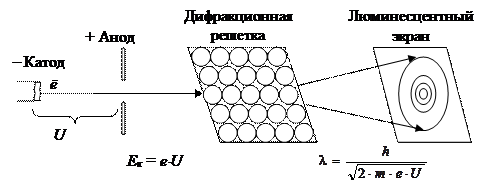Рис. 2‑2 Схема опыта дифракции электронов: U (В) – напряжение ускоряющего электрического поля

Позднее наблюдали дифракцию и более тяжелых частиц, например протонов, нейтронов, атомов гелия.

Можно предположить, что и движению макрообъекта соответствует также волновой процесс. Движению тела массой m = 1г со скоростью v=1см/с соответствует волновой процесс с длиной волны l=6,6×10^-29м. Но нет таких дифракционных решеток, чтобы наблюдать этот процесс.

Корпускулярно-волновой дуализм свойств электрона,как и других микрообъектов, является первым фундаментальным положением, на котором строится волновая механика – механика объектов атомных и субатомных размеров.

Принцип неопределенности

Вторым фундаментальным положением, на котором строится волновая механика, является принцип неопределенности Гейзенберга. Поскольку электрон обнаруживает одновременно свойства волны и частицы, возникают трудности, связанные с измерением корпускулярных свойств электрона, а именно одновременного определения координат и импульса электрона.

Вернер Гейзенберг (Heisenberg) в 1927 г. сформулировал следующее положение: для микрочастицы невозможно одновременно точно определить ее координаты и импульс. Ограничения в точности определения даются соотношением Гейзенберга:

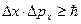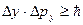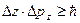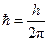, , , – постоянная Планка.

Из принципа неопределенности следует вероятностный подход к описанию механики микрообъектов. Точное определение координат частицы и ее импульса заменяется определением вероятности нахождения частицы в какой-то области пространства. Для движущейся частицы с вполне определенной энергией, а следовательно, и импульсом мы не можем указать точные значения координат (траектории движения), а можем говорить лишь о вероятности нахождения ее в какой-либо части пространства.

Вероятностный характер механики микрочастиц следует также из опытов по дифракции электронов. Если пропускать не поток, а последовательно по одному электрону, то каждый из них попадет в какое-то определенное место экрана и дифракционной картины не будет. В какое конкретное место попадет следующий электрон, мы не знаем, но знаем, где вероятность его появления максимальна (кольцо) и где минимальна (между кольцами) рис. 2.2. И только большое число электронов, пропущенных последовательно друг за другом, создадут на экране дифракционную картину.

Основные понятия волновой механики

Волновое уравнение

Уравнение, которое будет описывать движение электрона, должно удовлетворять следующим требованиям: отражать волновой характер движения электрона и содержать характеристики электрона как частицы.

Для описания волновых свойств электрона можно использовать известное из математики и физики дифференциальное уравнение второго порядка (уравнение волнового процесса):

^,

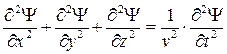v – скорость распространения волны.

Y(x,y,z,t) – пси-функция – волновая функция, которая зависит от координат и времени и может быть представлена в виде синуса, косинуса, экспоненты или любой другой функции, являющейся решением дифференциального уравнения волнового процесса.

Для простоты написания левую часть уравнения представляют обычно в операторной форме:

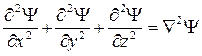
где 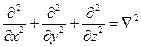– оператор Лапласа (читается "набла два"), тогда волновое уравнение приобретает вид:

.

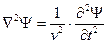Чаще всего интерес представляют стационарные процессы (стоячие волны). Описывающее их уравнение содержит функцию, не зависящую от времени. Для стоячей волны уравнение имеет вид:

ѲY(x,y,z) + (4p²n²/v²)×Y(x,y,z) = 0.

Поскольку частота волнового процесса (ν) равна скорости распространения волны (v), деленной на длину волны: 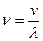, и соответственно 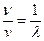, то

ѲY(x,y,z) + (4p²/l²) ×Y(x,y,z) = 0

В полученном уравнении, используя соотношение де Бройля, можно заменить длину волны такими характеристиками частицы, как масса и кинетическая энергия.

Длина волны де Бройля .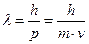

Кинетическая энергия электрона ,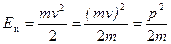

,

.

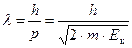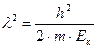
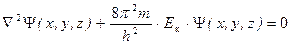Как правило, при описании состояния электрона определяют его полную энергию. Поскольку кинетическая энергия электрона (E_к) равна разности между полной (E) и потенциальной энергией (V): E_к = E – V, то можно записать

.

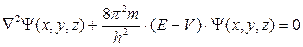Таким образом, получают волновое уравнение, независимое от времени, содержащее в качестве параметра массу электрона. Это уравнение известно как уравнение Шрёдингера, названное по имени австрийского физика Эрвина Шрёдингера (Schrödinger), который его предложил в 1926 г. для описания состояния микрочастицы в потенциальном поле.

Прежде чем решать уравнение Шрёдингера для конкретных систем, выясним физический смысл волновой функции. Раскрыть его достаточно непросто, поскольку в макромире нет аналогий корпускулярно-волновым свойствам микрообъектов. И до некоторой степени волновая функция представляет собой математическую абстракцию.

В 1926 г. Макс Борн (Born), применив вероятностные идеи принципа неопределенности, дал общепринятую в настоящее время трактовку физического смысла волновой функции: квадрат волновой функции пропорционален вероятности нахождения (dP) частицы в элементарном объеме (dV).

dP = Y²(x,y,z)×dV.

Примечание. В общем случае, если Y-функция комплексная величина, вероятность нахождения частицы (dP) в элементарном объеме (dV) пропорциональнаквадрату ее модуля: dP = |Y|²×dV = Y*∙Y×dV

Величина 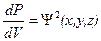называется плотностью вероятности и характеризует вероятность нахождения частицы в элементарном объеме пространства с координатами x,y,z. Для электрона ее часто называют электронной плотностью.

Вероятность нахождения частицы в каком-либо конечном объеме V равна интегралу квадрата волновой функции по данному объему:

.

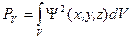Вероятность должна выражаться действительным положительным числом, меньшим или равным единице. Сама же волновая функция может быть положительной, отрицательной или мнимой, поэтому в общем виде используется не ее квадрат волновой функции, а произведение комплексно сопряженных функций.

Вероятностное толкование физического смысла волновой функции является одним из постулатов квантовой механики. Правомерность такой интерпретации подтверждается соответствием экспериментально определенного взаимного расположения атомов в молекулах и квантово-механического расчета.

Из условия, что вероятность события не может быть больше единицы, следует принцип нормирования волновых функций. Вероятность нахождения частицы во всем рассматриваемом объеме должна быть равна единице (частица находится в этом объеме – событие достоверное):

,

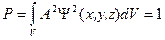А – нормирующий множитель, коэффициент, входящий в волновую функцию, который подбирается таким образом, чтобы выполнялось условие нормировки.

1.5.2 Решение уравнения Шрёдингера для простейших случаев

Решение уравнения Шрёдингера даже для относительно простых реальных объектов, таких как атомы и молекулы, содержащих два и более электронов представляет собой сложную математическую задачу. Для того чтобы понять характер и особенности результатов квантово-механического описания состояния электрона в атомах и молекулах, решим строго простейшую задачу нахождения электрона в так называемом "потенциальном ящике" – некоторой ограниченной области пространства, вне которой потенциальная энергия электрона обращается в бесконечность. Электрон не может покинуть пределы "потенциального ящика", то есть находится в связанном состоянии. Это, по сути своей, является моделью нахождения электрона в атоме.

Электрон в одномерном потенциальном ящике.

Рассмотрим состояние электрона в одномерном потенциальном ящике.

Движение электрона происходит только вдоль оси X (рис. 2.3). Внутри ящика потенциальная энергия частицы принимается равной нулю (потенциальную энергию можно отсчитывать от любого выбранного уровня), вне его она равна бесконечности, то есть частица находится внутри ящика и не может покинуть его пределы.

С точки зрения классической механики частица, находящаяся в потенциальном ящике, может иметь в принципе любую энергию и находиться в любой точке ящика. При квантово-механическом рассмотрении ситуация меняется. Состояние электрона описывает уравнение Шрёдингера, и его характеристики (энергия и вероятность нахождения в пространстве) получают при решении этого уравнения.

Рис. 2‑3. Электрон в одномерном потенциальном ящике: a − параметр (размер) потенциального ящика

Как и любое дифференциальное уравнение, уравнение Шрёдингера имеет бесконечное множество решений, но физический смысл имеют лишь некоторые из них. В нашем случае волновая функция описывает реальную физическую систему, поэтому она должна соответствовать определенным условиям:

конечность – вероятность нахождения электрона в пространстве не может быть больше единицы;

однозначность – вероятность нахождения электрона в точке однозначна;

непрерывность – нет особых точек в пространстве.

Поскольку электрон находится внутри одномерного «ящика» (V=0), уравнение Шрёдингера приобретает вид

.

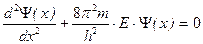Известно, что решением данного типа уравнения может быть функция 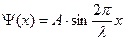– общее решение. В принципе вид функции может быть и другим.

Используя общее решение, граничные условия нашей задачи и принцип нормировки, можно получить волновую функцию, описывающую состояние электрона в потенциальном ящике.

Граничными условиями является равенство волновой функции нулю на стенках: , .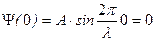

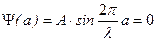Поскольку амплитуда волновой функции не равна нулю, то из второго условия следует:

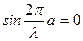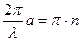, , n=1,2,3…, , .

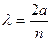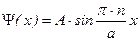Значение амплитуды А находят из условия нормировки. Поскольку электрон находится в потенциальном ящике, то интеграл квадрата волновой функции по координате ящика (от 0 до a) равен единице:

, , ,

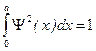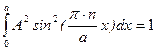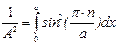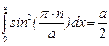
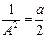
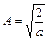
Таким образом, выражение для волновой функции электрона в одномерном потенциальном ящике имеет вид

,

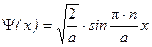где a – параметр потенциального ящика; n = 1,2,3…– целочисленный параметр. То есть состоянию электрона в потенциальном ящике соответствует набор волновых функций, отличающихся целочисленным параметром n, называемым квантовым числом.

Для определения энергии электрона проделаем следующие математические операции.

1. Поскольку в уравнение Шрёдингера входят волновая функция, и ее вторая производная, запишем их:

,

,

.

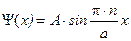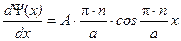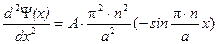2. Подставим выражения волновой функции и ее второй производной в уравнение Шрёдингера, описывающее состояние электрона внутри потенциального ящика:

,

.

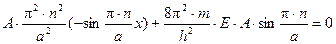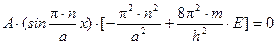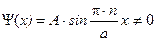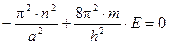3. Поскольку волновая функция внутри ящика не равна нулю ( ), то , и

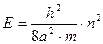, n=1,2,3…

Следовательно,набору волновых функций соответствует набор величин энергий (рис.2.4).

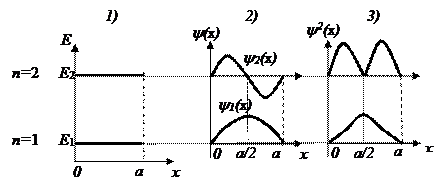
Рис. 2‑4. Первое и второе энергетическое состояние электрона в одномерном потенциальном ящике. Полная энергия Е_i (1), соответствующая ей волновая функция Y_i(x) (2) и плотность вероятности Y_i²(x) (3) электрона

Из полученных результатов решения следуют особенности квантово-механического описания состояния электрона в потенциальном ящике:

1. Электрон, находясь в потенциальном ящике, может иметь только дискретные значения полной энергии E₁, E₂, E₃…, величины которых определяет целочисленный параметр n = 1,2,3…, называемый квантовым числом. То есть энергия связанного электрона квантована.

2. Распределение вероятности нахождения электрона в объеме потенциального ящика (плотность вероятности) определяется его энергией.

3. Величина энергии и соответствующая ей волновая функция, характеризующая распределение вероятности нахождения электрона в объеме (Е_i -Y_i), определяют энергетическое состояние электрона. Каждому энергетическому состоянию соответствует квантовое число (n).

Электрон в трехмерном потенциальном ящике. Вырожденные энергетические состояния.

Задача о нахождении частицы в трехмерном потенциальном ящике аналогична предыдущей задаче. Граничные условия полностью совпадают: волновая функция на границах ящика обращается в ноль, потенциальная энергия внутри ящика равна нулю (V=0), а за пределами ящика – бесконечности (V=¥), то есть частица не может покинуть потенциальный ящик. Единственным отличием является то, что волновая функция является функцией трех пространственных координат: Y(x,y,z).

Уравнение Шрёдингера для данного случая представляет собой дифференциальное уравнение в частных производных с тремя переменными:

^.

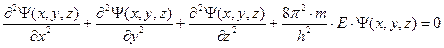Стандартным приемом, которым пользуются при решении такого типа уравнений, является разделение переменных: представление волновой функции в виде произведения трех функций, каждая из которых зависит только от одной координаты:

,

.

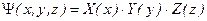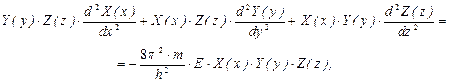
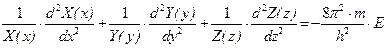Поскольку правая часть уравнения не зависит от координат, то можно представить полную энергию электрона как сумму трех энергий: E=E_x+E_y+E_z. Уравнение Шрёдингера при этом преобразуется в три дифференциальных уравнения, аналогичных волновым уравнениям электрона в одномерном ящике, решение которых уже получено:

,

,

.

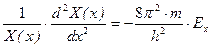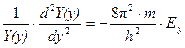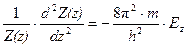Для волновой функции:

, , ,

,

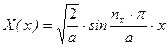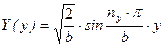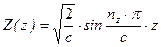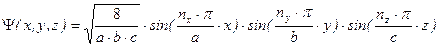a,b,c – параметры трехмерного потенциального ящика (размеры – длина, ширина, высота); n_x, n_y, n_z – целочисленные параметры – «квантовые числа». Необходимо отметить, что каждой координате соответствует свое квантовое число.

Для энергии:

, , ,

.

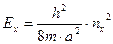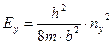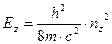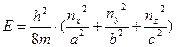Из полученных результатов решения следует:

1. Энергия электрона в трехмерном потенциальном ящике квантована.

2. Каждое энергетическое состояние электрона определяется набором из трех квантовых чисел.

Однако в реальных системах часто встречается ситуация, когда определенное энергетическое состояние (энергия частицы) может быть описано не единственным набором квантовых чисел, то есть более чем одной волновой функцией. Тогда говорят о вырождении энергетического состояния.

Проиллюстрировать явление вырождения по энергии можно на примере частицы в трехмерном потенциальном ящике. Если рассмотреть энергетические состояния частицы в ящике, который представляет собою куб (а=b=c), то выражение для энергии приобретает вид

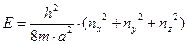
а – параметр куба (величина ребра).

Составим энергетическую диаграмму состояния частицы в таком ящике, откладывая по вертикальной оси энергию частицы в единицах 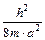(рис.2.5).

Рис. 2‑5. Энергетическая диаграмма электрона в трехмерном потенциальном ящике: [n_x, n_y, n_z] – набор квантовых чисел, соответствующий данному энергетическому состоянию

В кубическом потенциальном ящике почти все энергетические состояния в той или иной степени вырождены. Степень вырождения − число вариантов наборов квантовых чисел (число волновых функций), при помощи которых можно описать данное энергетическое состояние. Снятие вырождения является важной проблемой квантово-механического описания системы. В случае трехмерного потенциального ящика вырождение снимается частично (a=b¹c) или полностью (a¹b¹c) при изменении параметров ящика. В реальных системах проблема снятия вырождения является более сложной проблемой.

Энергетическое состояние электрона в кулоновском поле ядра достаточно близко соответствует ситуации нахождения электрона в трехмерном потенциальном ящике. Поэтому все закономерности, которые были получены, а главное дискретность энергетических состояний, распространяются и на атом.