Возбужденные состояния атома водорода
Полученное решение уравнения Шрёдингера для основного состояния атома водорода является частным случаем, когда волновая функция сферически симметрична и не зависит от угловых координат. Для атома водорода решениями уравнения Шрёдингера могут быть и другие функции более сложной симметрии.
В общем виде волновая функция в полярных координатах является функцией трех переменных 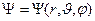 , поэтому уравнение Шрёдингера будет представлять собою дифференциальное уравнение с частными производными. Стандартный метод решения уравнения данного типа − метод разделения переменных.
, поэтому уравнение Шрёдингера будет представлять собою дифференциальное уравнение с частными производными. Стандартный метод решения уравнения данного типа − метод разделения переменных.
Полагают, что волновая функция 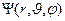 может быть представлена в виде произведения трех волновых функций, каждая из которых содержит только одну переменную:
может быть представлена в виде произведения трех волновых функций, каждая из которых содержит только одну переменную:
Y(r, J ,j) = R(r)×Q(J)×F(j),
где R(r) – функция радиального; Q(J)×и F(j) – функции углового распределения электронной плотности.
Часто две угловые функции заменяют одной функцией углового распределения Y(J ,j):
Y(r, J ,j) = R(r)×Y(J ,j).
Явный вид волновых функций, являющихся решениями уравнения Шрёдингера, содержит целочисленные параметры: R(r) – n, l, а Y(J,j) – l, m.
Таким образом, решением общего волнового уравнения является набор волновых функций, которые содержат в качестве целочисленных параметров три числа: n, l, m, которые получили названия главного (n), орбитального (l) и магнитного (m) квантовых чисел. Квантовые числа характеризуют энергетические состояний электрона в атоме водорода.
Физический смысл квантовых чисел.
n − главное квантовое число – определяет разрешенные (дискретные, квантовые) значения полной энергии электрона, характеризует размер электронных орбиталей (соответственно является мерой расстояния между электроном и ядром).
Решение уравнения Шрёдингера дает следующее выражение для возможных значений полной энергии электрона в атоме водорода:
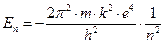 .
.
Главное квантовое число может принимать целочисленные значения от единицы до бесконечности: n = 1,2,3,4…¥.
l – орбитальное квантовое число – определяет возможные квантовые значения орбитального момента количества движения электрона, то есть связано с его кинетической энергией.Пространственная конфигурация (форма) электронной орбитали связана со значением орбитального квантового числа. Возможные величины l соответствуют n и могут принимать целочисленные значения от 0 до n–1: l = 0,1,2,3...(n–1).
Исторически сложилось, что численным значениям l соответствуют буквенные обозначения: l = 0 – s; l = 1 – p; l = 2 – d; l = 3 – f и т. д. Они соответствуют также электронам, их волновым функциям, орбиталям и энергетическим состояниям.
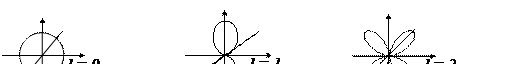 Пространственная конфигурация простейших орбиталей (форма) показана на рис.2.10: s-орбиталь (l = 0) – сферически симметричная; p-орбиталь (l = 1), d-орбиталь (l = 2), f-орбиталь (l = 3) и т.д имеют более сложную пространственную симметрию.
Пространственная конфигурация простейших орбиталей (форма) показана на рис.2.10: s-орбиталь (l = 0) – сферически симметричная; p-орбиталь (l = 1), d-орбиталь (l = 2), f-орбиталь (l = 3) и т.д имеют более сложную пространственную симметрию.
Рис. 2‑10 Пространственная конфигурация простейших орбиталей
m–магнитное квантовое число– определяет разрешенные направления в пространстве вектора орбитального момента количества движения. Возможные значения m определяются для каждого значения l и могут принимать целочисленные значения от от +l до -l: m = +l, (l-1),...,0,...,(-l+1), -l.
Набор значений mопределяет числовозможных ориентаций s, p, d, … орбиталей в пространстве для данного числа n. Поскольку потенциальная энергия частицы зависит от ее положения в пространстве, то магнитное квантовое число связано с потенциальной энергией электрона.
s-орбитали (l=0) – магнитное квантовое число принимает единственное значение m=0 – единственный способ ориентации в пространстве (сферически-симметричная орбиталь).
p-орбитали (l=0) – магнитное квантовое число принимает три возможных значения m=+1,0,-1 – три возможных способа ориентации орбитали в пространстве (рис.2.11).

Рис. 2‑11 Возможные ориентации p-орбитали в пространстве
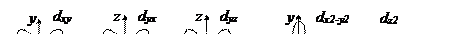 d-орбитали (l=2) – магнитное квантовое число принимает пять возможных значений m=+2,+1,0,-1,-2 – пять возможных способов ориентации орбитали в пространстве (рис. 2.12).
d-орбитали (l=2) – магнитное квантовое число принимает пять возможных значений m=+2,+1,0,-1,-2 – пять возможных способов ориентации орбитали в пространстве (рис. 2.12).
Рис. 2‑12 Возможные ориентации d-орбитали в пространстве
Электронные орбитали атома водорода.
Поскольку электронную орбиталь характеризует набор трех квантовых чисел, то все возможные электронные орбитали атома водорода, получают путем различных комбинаций квантовых чисел. Для первых четырех значений главного квантового числа возможные орбитали (энергетические состояния электрона) приведены в таблице и на энергетической диаграмме (рис. 2.13).
| n | l=0,1,2…(n-1) | m=+l, (l–1),...0...(– l+1),-l | Энергия орбитали | Число орбиталей |
| 0 – s | E1 | |||
| 0 – s 1 – p | +1,0,-1 | E2 | ||
| 0 – s 1 – p 2 – d | +1,0,-1 +2,+1,0,-1,-2 | E3 | ||
| 0 – s 1 – p 2 – d 3 – f | +1,0,-1 +2,+1,0,-1,-2 +3,+2,+1,0,-1,-2,-3 | E4 |
Обозначение орбитали складывается из цифры, которая указывает главное квантовое число, и буквы, указывающей тип орбитали (орбитальное квантовое число). Например, 5р – это орбиталь, имеющая n=5 и l=1. Графически орбитали изображают в виде черточек или прямоугольников.

Рис. 2‑13 Диаграмма энергетических состояний электрона в атоме водорода
На приведенной диаграмме видно, что для атома водорода энергетические состояния электрона вырождены по орбитальному и магнитному квантовым числам (энергия электрона зависит только от главного квантового числа):
E1s < E2s = E2p< E3s = E3p = E3d < E4s = E4p = E4d = E4f < …
Спиновое квантовое число.
Кроме трех квантовых чисел имеется четвертое – спиновое (ms), которое не входит в решения уравнения Шрёдингера для атома водорода.
В модели Джорджа Уленбека (Uhlenbeck) и Самуэла Гаудсмита (Goudsmit)спиновое квантовое число характеризует собственный момент количества движения и может принимать только два значения ±½, которые соответствуют вращению электрона вокруг собственной оси по или против часовой стрелки. Это вращение создает собственный магнитный момент электрона, взаимодействие которого с магнитным полем атома приводит к двум возможным энергетическим состояниям.
В 1933 г. Поль Дирак (Dirac) описал состояние электрона в атоме с учетом релятивистских эффектов (привел в соответствие представления Шрёдингера с теорией относительности Эйнштейна). Полученные решения содержат кроме трех квантовых чисел четвертый параметр –спиновое квантовое число (mS).
Радиальное распределение электронной плотности.
В квантово-механической модели атома не существует понятия траектории движения электрона, оно заменено на вероятность нахождения электрона в элементарном объеме пространства, а каким образом туда попадает электрон, не определяется. Так же как и для основного состояния, для возбужденных состояний имеются функции радиального распределения электронной плотности:
s(r) 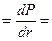 y2×4pr2.
y2×4pr2.
Графический вид функций приведен на рис. 2.14. Площадь под любой кривой радиального распределения равна единице, поскольку она равна вероятности нахождения электрона во всем объеме:
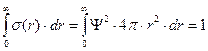 .
.
Рис. 2‑14
 |
Функции радиального распределения электронной плотности для различных энергетических состояний атома водорода
В радиальном распределении 1s электрона имеется один максимум на расстоянии, равном первому боровскому радиусу (1/a = 0,53Å). Число максимумов в функции распределения ns электронов (n>1) равно n, 2s – два максимума, 3s – три максимума и т.д.
Функции радиального распределения для p, d, f-электронов подобны функциям для s электронов, с учетом того, что число максимумов равно n–l: 1s, 2p, 3d...– функции радиального распределения с одним максимумом, 2s, 3p, 4d...– с двумя, 3s, 4p, 5d.. – с тремя максимумами.
Из приведенных рисунков видно, что, во-первых, положение главного максимума, расстояние от ядра до области с максимальной вероятностью нахождения электрона, определяется в основном главным квантовым числом n, то есть можно говорить о том, что n характеризует «расстояние электрона до ядра». Во-вторых, для электронов, находящихся в состояниях с одинаковым главным квантовым числом, вероятность нахождения электрона вблизи ядра уменьшается с увеличением орбитального квантового числа (иногда говорят о различной «проникающей способности» орбиталей). Это имеет большое значение при рассмотрении многоэлектронных атомов.
Различия в проникающей способности орбиталей можно проиллюстрировать также зависимостью вероятности нахождения электрона в объеме сферы радиуса r в зависимости от ее радиуса (рис. 2.15):
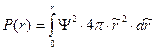 .
.

Рис. 2‑15 Вероятность нахождения электрона атома водорода в объеме сферы радиуса r, занимающего 3s, 3p или 3d-орбиталь
Дата добавления: 2017-02-20; просмотров: 4216;
