Многоэлектронные атомы
В случае многоэлектронного атома (число электронов два и более) получить точные решения уравнения Шрёдингера невозможно (сложно), поскольку необходимо учитывать энергию взаимодействия электронов не только с ядром, но и между собой. Поэтому при определении волновых функций и энергетических состояний используют приближенные методы. В частности, при описании системы рассматривают движение одного электрона в эффективном поле, которое образуется полем ядра и полем остальных электронов. При этом используют понятие эффективного заряда ядра.
Эффективный заряд ядра (Zэ) равен заряду ядра (Z) за вычетом константы экранирования (s) –постоянной величины, учитывающей влияние остальных электронов атома на рассматриваемый электрон: Zэ = Z - s. При таком приближенном рассмотрении состояние электрона описывается волновыми функциями, подобными тем, которые были получены для атома водорода. Увеличение заряда ядра и различия в радиальном распределении электронной плотности для электронов, находящихся на различных орбиталях, приводят к изменению энергии орбиталей по сравнению с атомом водорода. Отличия заключаются в следующем.
1. Увеличение заряда ядра приводит к возрастанию энергии притяжения электрона к ядру и соответственно к понижению энергии электронной орбитали (рис. 2.16).

Рис. 2‑16 Схема изменения энергии орбиталей в зависимости от Z
2. Вследствие различного радиального распределения электронной плотности s, p, d, f-электронов величина константы экранирования зависит не только от числа электронов, создающих эффективный заряд ядра, но и от типа орбиталей, которые они занимают. Понижение энергии орбиталей с ростом заряда ядра (для одного значения n) различно для s, p, d, f-состояний, что приводит к снятию вырождения по орбитальному квантовому числу.
3. Вследствие снятия вырождения по орбитальному квантовому числу энергия электрона определяется не только главным квантовым числом n, но и орбитальным l.
Пример. Константа экранирования (s) и эффективный заряд ядра (Zэ) атомов для первых 11 элементов периодической таблицы:
| Атом | H | He | Li | Be | B | C | N | O | F | Ne | Na |
| Z | |||||||||||
| s | 0,3 | 1,70 | 2,05 | 2,40 | 2,75 | 3,10 | 3,45 | 3,80 | 4,15 | 8,80 | |
| Zэ=Z-s | 1,7 | 1,30 | 1,95 | 2,60 | 3,25 | 3,90 | 4,55 | 5,20 | 5,85 | 2,20 |
Энергия орбитали 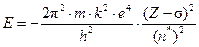 ,
,
Z – s = Zэ – эффективный заряд ядра; n* – эффективное главное квантовое число, s; Zэ; n* вычисляют по правилам, разработанным Джоном Слэтером (Slater).
Таким образом, получают последовательность энергетических состояний в многоэлектронном атоме (стационарные состояния реально существующих атомов):
E1s<E2s<E2p<E3s<E3p<E4s<E3d<E4p<E5s<E4d<E5p<E6s<E4f<…
 Эту последовательность можно проиллюстрировать диаграммой энергетических состояний электронов в многоэлектронном атоме с определенным значением Z (рис. 2.17). Диаграмма показывает энергетическое положение орбиталей относительно друг друга в атоме с определенным зарядом ядра Z, но не их абсолютные значения.
Эту последовательность можно проиллюстрировать диаграммой энергетических состояний электронов в многоэлектронном атоме с определенным значением Z (рис. 2.17). Диаграмма показывает энергетическое положение орбиталей относительно друг друга в атоме с определенным зарядом ядра Z, но не их абсолютные значения.
Рис. 2‑17 Диаграмма энергетических состояний невозбужденного многоэлектронного атома
 Каждый последующий атом в периодической системе отличается от предыдущего тем, что заряд его ядра увеличивается на единицу и соответственно на единицу увеличивается число электронов. Каждому электрону должно соответствовать свое энергетическое состояние, которое описывается четырьмя квантовыми числами. В изолированных многоэлектронных атомах энергетические состояния электронов вырождены по магнитному и спиновому квантовому числу. В электромагнитном поле (внешнее поле или поле окружающих атомов) это вырождение может сниматься (рис. 2.18).
Каждый последующий атом в периодической системе отличается от предыдущего тем, что заряд его ядра увеличивается на единицу и соответственно на единицу увеличивается число электронов. Каждому электрону должно соответствовать свое энергетическое состояние, которое описывается четырьмя квантовыми числами. В изолированных многоэлектронных атомах энергетические состояния электронов вырождены по магнитному и спиновому квантовому числу. В электромагнитном поле (внешнее поле или поле окружающих атомов) это вырождение может сниматься (рис. 2.18).
Рис. 2‑18 Схема снятия вырождения для s и р энергетических состояний в электромагнитное поле
Периодический закон и таблица элементов
Дата добавления: 2017-02-20; просмотров: 1331;
