Расчет жесткости и прочности
Балка должна удовлетворять требованию жесткости, т. е. ее прогиб fmах от наибольшей нагрузки не должен превышать предельно допускаемого. Обычно в балках предельное значение отношений fmах/L регламентируется нормами. Норма жесткости для балок разных назначений различна, например, в подкрановых балках fmах/L < 1/600-1/700; в главных балках междуэтажных перекрытий fmах/L = 1/400.
Чтобы удовлетворить требованиям жесткости, балка должна иметь высоту не менее некоторой предельной. Эта минимальная высота определяется видом нагружения и допускаемыми напряжениями. Рассмотрим, какова должна быть наименьшая высота балки, свободно лежащей на двух опорах, если она нагружена равномерной нагрузкой (рис. 9.3 а).
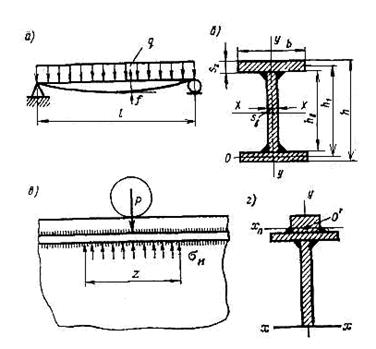
Рис.9.3. К расчету сварной балки:
а – изогнутая ось балки от нагрузки q; б – поперечное сечение балки; в, г – влияние сосредоточенной силы
Расчетный прогиб
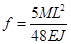 , (9.1)
, (9.1)
где EJ - жесткость балки.
Для рассматриваемой балки расчетный момент
M = qL2/8. (9.2)
Подставляя значение М в формулу (11.1), получим
 . (9.3)
. (9.3)
Изгибающий момент
M=[σ]р W, (9.4)
где [σ]р - допускаемое напряжение; W - момент сопротивления.
Если расчетное сечение симметрично относительно горизонтальной оси, то W=2J/h,где h - высота балки.
Подставим значение М из формулы (9.4) в формулу (9.3):
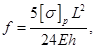 (9.5)
(9.5)
откуда
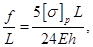
или 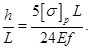 (9.6)
(9.6)
Высота балки, вычисленная по формуле (9.6), является наименьшей при заданных [σ]р и f/L и может быть увеличена, если это диктуется соображениями компоновки конструкции или экономии металла. При других нагружениях и системах балок, например, консольных, многоопорных, с защемленными концами и т. п., в формуле (9.6) изменяется лишь числовой коэффициент. В общем случае
 . (9.7)
. (9.7)
Коэффициенты ψ для балок из низкоуглеродистых сталей приведены в табл.9.1.
Таблица 9.1
Значение коэффициента ψ для балок с различной схемой нагружения
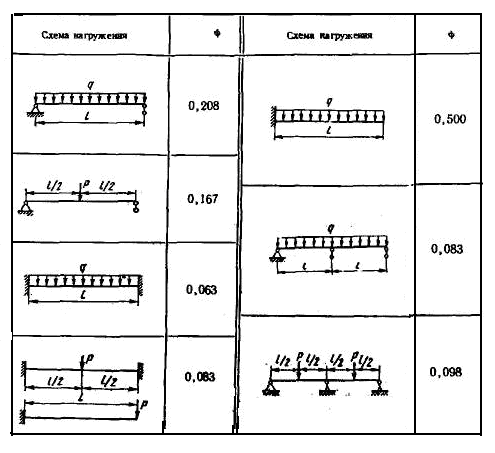
Балки из стали Ст3 для различных элементов конструкций имеют следующие предельные отношения fmax/L, указанные в табл. 9.2.
Таблица 9.2
Предельные отношения fmax/L
| Назначение балок | Предельные Отношения fmax/L |
| Подкрановые балки: | |
| - при ручных кранах | 1/500 |
| - при электокранах грузоподъемностью до 50 т | 1/600 |
| - при электокранах грузоподъемностью > 50 т | 1/750 |
| Монорельсовые пути | 1/400 |
| Балки рабочих площадок производственных зданий: | |
| - главные при отсутствии рельсовых путей | 1/400 |
| - при наличии узкоколейных путей | 1/400 |
| - при наличии ширококолейных путей | 1/600 |
| - прочие | 1/250 |
| Балки междуэтажных перекрытий: | |
| - главные | 1/400 |
| - прочие | 1/250 |
| Балки покрытий и чердачных перекрытий: | |
| - главные | 1/250 |
| - прогоны | 1/200 |
При действии моментов в двух плоскостях (вертикальной и горизонтальной) высота балки h определяется с учетом напряжения от моментов Мх и Mv. Сумма (σx+σv) должна быть меньше [σ]p. Соотношение между σx и σv устанавливается приближенно на основе имеющегося опыта проектирования конструкции или методом последовательного приближения. При этом задаются ожидаемыми отношениями σx/σv и затем проверяют их правильность повторными расчетами.
Балка должна удовлетворять прочности при условии наименьшей массы, т. е. поперечное сечение должно быть минимальным.
Высота балки для двутаврового профиля может быть найдена по формуле
h = (1,3-1,4)√М/(SB[σ]p), (9.8)
а для коробчатого
h = √М/(SB[σ]p), (9.9)
где SB - толщина вертикального листа.
При проектировании балок толщина SB в формулах (9.8) и (9.9) неизвестна. Поэтому ее первоначально задают. Для разных строительных конструкций SB обычно изменяется в сравнительно узких пределах.
Можно принимать
SB=√10hв/12,5; (9.10)
для тяжелых конструкций
SB=7+ 0,005hв, (9.11)
где SB и hв (рис. 9.3 б) выражены в мм.
Значения h, найденные с учетом требований достаточной жесткости и прочности, а также при условии наименьшей массы, могут оказаться совершенно различными. Из двух значений, вычисленных для балки двутаврового профиля по формулам (9.6) и (9.7) или (9.8) и (9.9), следует принять большее или во всяком случае не меньшее, чем при вычислении по формулам (9.6) и (9.7). Далее подбирают размеры поперечного сечения балки с учетом расчетного изгибающего момента М и высоты h.
Рассмотрим процесс подбора сечения двутаврового профиля (рис. 9.3 б). Для этого найдем требуемый момент сопротивления:
Wтр =М/[σ]p (9.12)
и требуемый момент инерции сечения:
Jтр=Wтрh/2. (9.13)
Вычислим момент инерции Jв вертикального листа высотой hв и толщиной SB. Принимаем hв=0,95h.
Находим требуемый момент инерции двух горизонтальных листов:
Jг=Jтр-Jв. (9.14)
В другой форме момент инерции выразится так:
Jг =2[J0+Fг(h1/2)2], (9.15)
где Jг - момент инерции горизонтального листа относительно собственной оси, который всегда очень мал и может быть принят равным нулю;
h1 - расстояние между центрами тяжести горизонтальных листов, которое можно принять равным (0,95 - 0,98) h.
Из уравнения (9.15) находим требуемую площадь сечения одного горизонтального листа:
Fг=2Jг/h21. (9.16)
Подобрав размеры поперечного сечения балки, определим напряжения и таким образом проверим, удовлетворяют ли подобранные размеры условиям прочности.
Напряжение от изгиба
σ =Mh/(2J)<[σ]p. (9.17)
Касательное напряжение от поперечной силы будет
τ =QS/(J∙SB) ≤[τ], (9.18)
где Q - наибольшая поперечная сила балки; S - статический момент полуплощади сечения (симметричного) относительно центра тяжести балки (рис. 9.3 б).
Эквивалентные напряжения проверяются обычно в тех случаях, когда максимальные значения М и Q совпадают по длине балки в одном сечении. Их определяют на уровне верхней кромки вертикального листа:
σэ = √σ21 + 3τ2. (9.19)
Здесь нормальное напряжение
σ1= Мhв/(2·J) (9.20)
и касательное напряжение
τ1=QS1/ (J∙SB), (9.21)
где S1- статический момент площади горизонтального пояса относительно центра тяжести сечения балки.
В большинстве случаев эквивалентные напряжения σэ оказываются меньше σ, вычисленного по формуле (9.17).
Допустим, что к верхнему поясу балки прикладывают сосредоточенные перемещающиеся грузы (рис. 9.3 в). Это имеет место в крановых, подкрановых и мостовых балках. При этом определяют прочность вертикального листа с учетом местного напряжения под грузом:
σм=mP/(SB·z),(9.22)
где коэффициент m=1,5 при тяжелом режиме работы балки (например, в металлургических цехах), m=1при легком режиме (в ремонтных цехах и т. п.); z- условная длина, на которой сосредоточенный груз распределяется в вертикальном листе (рис. 9.3 в):
z=3,253√Jп/SB (9.23)
Здесь Jп - момент инерции горизонтального листа совместно с приваренным к нему рельсом (если таковой имеется) относительно оси хп, проходящей через их общий центр тяжести О' (рис. 9.3 г).
Дата добавления: 2018-03-02; просмотров: 5048;
