Пример расчета и конструирования балки

Требуется разработать конструкцию сварной балки пролетом l=16 м со свободно опертыми концами. Допускаемое напряжение в подкрановых балках устанавливают с учетом коэффициентов условий работы m=0,9 и перегрузки n=1,2:

[σ]_р = R_рm/n.

Для стали Ст3 при R_р=210 МПа [σ]_р = 157,5 МПа≈160 МПа.

Балка нагружена равномерной нагрузкой от собственного веса q=2,5 кН/м и двумя сосредоточенными грузами Р=50 кН (от веса тележки с грузом), которые могут перемещаться по балке. Расстояние между осями тележки d=2 м; наибольший прогиб балки f от сосредоточенных грузов не должен пре­вышать 1/500 ее пролета l (рис. 9.9 а).

Конструирование балки следует начать с определения расчетных усилий М и Q. Сначала необходимо построить линии влияния моментов, чтобы знать их максимально возможные значения в разных сечениях балки (рис. 9.9 б). Метод линий влияния рассмотрен в главе 3 [Статика сооружений стержневых и балочных систем]. Максимальные ординаты y_max линий влияния для различных сечений х при наиболее опасном положении грузовой тележкисоставят:

х . .. 0,1l 0,2l 0,3l 0,4l 0,5l

y_max.. 0,09l 0,16l 0,21l 0,24l 0,25l

Определим моменты от веса тележки в каждом из сечений с учетом того, что один из сосредоточенных грузов располагается над вершиной линии влия­ния, а второй занимает положение, показанное на рис. 10.9 б. Момент от сосредоточенных сил вычисляется по формуле

M_p = Σ P·y_i (9.37)

где y_i- ордината линии влияния, т. е.

M_p = y_max [1 + (l - x - d)/( l - x)] P. (9.38)

Момент в сечении х от равномерно распределенной нагрузки q (рис. 9.9 а)

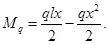(9.39)

Суммарные моменты в сечениях от сосредоточенных сил и равномерной на­грузки

M_Σ = M_p + M_q (9.40)

Результаты подсчетов по формулам (9.38), (9.39) и (90.40) представлены на рис. 9.9 в, г, д. Таким образом, расчетное значение момента для балки составляет

M_Σ = 430 кН·м=0,43 МН·м. Требуемый момент сопротивления балки для этого изгибающего момента равен

W_Tp= M_Σ /[σ]_р = 0,43:160= 0,002688 м³ = 2688 см³.

Производим построение линии влияния поперечной силы (рис. 9.9 е). Ординаты Q для различных сечений х составят:

х 0 0,1l 0,2l 0,3l 0,4l 0,5l

Q 1 0,9 0,8 0,7 0,6 0,5

Определим расчетные усилия от сосредоточенных сил в каждом из указан­ных сечений с учетом того, что одна из сил располагается над вершиной линии влияния:

Q_p = Σ P _yi , т. е.

Q_p=[1 + (l - х - d)/(l - x)]P. (9.41)

Поперечные силы Q_q от собственного веса q равны

Q_q=ql/2-qx. (9.42)

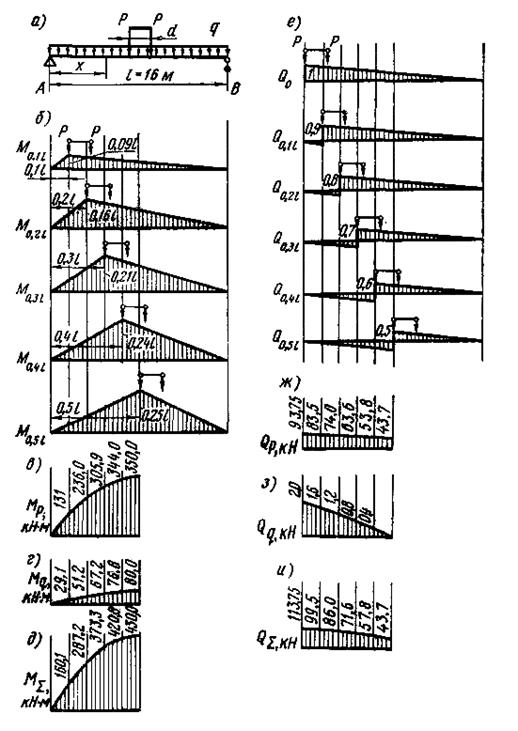
Рис.9.9. К расчету балки пролетом 16 м:

а — схема балки; б — линии влияния; в — наибольший момент М от подвижной нагрузки в разных сечениях; г — эпюра М от q; д — наибольший расчетный момент М от сил Р и q в разных се­чениях; е — линии влияния поперечной силы Q; ж — наибольшие значения Q от подвижной нагрузки в разных сечениях; з — эпюра Q от q; и — наибольшие расчетные значения Q в разных сечениях

Суммарные значения поперечных сил от сосредоточенных и равномерно рас­пределенных нагрузок

Q_Σ = Q_P + Q_q. (9.43)

Результаты подсчетов представлены на рис. 9.9 ж, з, и.

Определив расчетные усилия, переходим к нахождению наименьшей высо­ты балки из условия нормы жесткости fmax/l =1/500 при сосредоточенных гру­зах Р. При определении требуемой высоты следует учесть что по условию прогиб ограничен лишь в отношении нагрузки Р. Так как напряжение от сум­марного момента M_Σ =430 кН·м достигает [σ]_p, то напряжение от момента М = 350 кН·м, вызванного сосредоточенными грузами, будет составлять 0,8[σ]_р. Этонапряжение следует брать вместо [σ]_р при определении требуемой высоты балок h.

Прогиб балки от двух сосредоточенных сил Р, расположенных симметрично в пролете (рис. 9.10 а),

f=Pal²[l-4/3(a/l)²]/(8EI). (9.44)

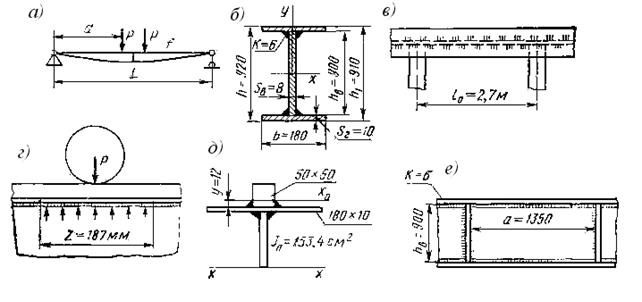
Рис.9.10. К примеру расчета сварной балки l=16 м:

а – определение высоты балки h из условий жесткости; б – подобранный профиль балки; в – расположение горизонтальных связей; г – учет местного влияния сосредоточенной силы; д – к расчету поясных швов; е – расстановка ребер жесткости

Подставив Р·а=М, получим

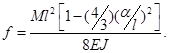(9.45)

Если выразить М в формуле (9.45) через напряжение, 0,8[σ]_р вызванное сосредоточенными силами и умноженное на момент сопротивления W=2J/h, то

f=1,6[σ]_р l² [l-(4/3)(a/ l)²]/(8Eh), (9.46)

откуда требуемая высота балки из условий жесткости

h/l = 0,8[σ]_pl[l-(4/3)(a/l)²]/(4 Ef)=0,8·160·500[l-(4/3)(7/16)²]/(4·2,1 ·10⁵) = 0,0567;

или h = 0,0567 · 16 м =0,912 м.

Чтобы определить требуемую высоту балки из условия ее наименьшего се­чения, нужно задаться толщиной вертикального листа. Можно воспользоваться рекомендуемым приближенным соотношением s_в= √10 h/ 12,5 = 7,6 мм.

Примем s_в = 8 мм.

Требуемая высота из условия наименьшей массы по формуле

h = 1,3 √0,43/(8·160·10^-3) = 0,75 м.

Так как требуемая высота, найденная по формуле (9.46), больше чем 0,75 м, то ее и следует принять в расчет при подборе сечения. Высоту вертикального листа h_в принимаем равной 90 см, а вы­сота балки h=92 см (рис. 9.10 б).

Требуемый момент инерции поперечного сечения сварной балки двутавро­вого профиля

I_тр = W_трh/2 = 2688·46 = 123648 см⁴

Момент инерции подобранного вертикального листа 900x8 мм

J_в = 90³·0,8/12 = 48600 см⁴. Требуемый момент инерции горизонтальных листов балки (поясов) J_г=J_тр - J_в = 123648 – 48600 = 75 048 см⁴. Момент инерции горизонтальных листов записывается в виде

J_г=2[I₀+F_г(h₁/2)²].

Величина I₀= h_в· s_в³/12= 90·0,8³/12 = 3,84 см⁴ ≈ 0.

Таким образом, требуемое сечение одного пояса балки равно

F_г = J_г/[2(h₁ /2)² = 75048 /(2·45,5²) = 18,1 см².

Принимаем сечение горизонтального листа 180x10 мм.

Определим уточненное значение момента инерции подобранного поперечного сечения балки:

J=90³·0,8/12 + 2 (1³·18/12 + 1 · 18· 45,5²) =48600 + 74532 = 123132 см⁴. Наибольшее нормальное напряжение в крайнем волокне балки

σ_max = М· y_max /J =0,43 · 0,46 / 123132 · 10^-8 =160,7 МПа.

Расчетное напряжение превышает допускаемое на 0,5%, что вполне приемлемо.

Определим касательное напряжение на уровне центра тяжести балки в опор­ном ее сечении по формуле τ =QS/(J·s_b):

S= 18·45,5 + 0,8·45²/2=819 + 810 = 1 629 см³;

Q= 113,75 кН;

τ = 0,11375 ·1629 · 10^-6 /(123132 · 10^-8·0,8 · 10^-2) = 19 МПа.

Определим эквивалентные напряжения в сечении, в котором наибольший изгибающий момент М=0,43 МН·м и поперечная сила Q = 43,7 кН. Эквивалент­ные напряжения вычисляются на уровне верхней кромки вертикального листа в зоне резкого изменения ширины сечения. Вычислим в этом волокне балки на­пряжения от момента М:

σ₁ = М h_в /(2J)=0,43·0,92/(2·0,00123132) =157,2 МПа. В этом же волокне напряжение от поперечной силы Q

τ₁ = QS/ J·s_B= 0,0437·819·10^-6/(0,00123132·0,8·10^-2) = 3,65 МПа.

Здесь S=18·l ·45,5 = 819 см³ - статический момент площади сечений горизонтального листа относительно центра тяжести.

Эквивалентное напряжение определяется по формуле

σ_экв = √σ²₁ + 3 τ²₁= 157,4 МПа,

что меньше наибольшего нормального напряжения в крайнем волокне.

Рассмотрим, как обеспечить общую устойчивость балки. Если ее не закрепить в горизонтальной плоскости, то потребуется значительное уменьшение допускаемых напряжений. Поэтому следует предусмотреть закрепления от воз­можных перемещений верхнего пояса, например, установить горизонтальные связи.

Зададимся расстоянием между закреплениями l_о= (10-20)b, например, 2,7 м (рис. 9.10 в).

По формуле (9.26): α = 8[270·1/(18 ·92)]²·[1+ (90·0,8³)/(2·18·1³)] = 0,49.

По графику, приведенному на рис. 9.5, пользуясь интерполяцией, определяем коэффициент ψ при α = 0,49, коэффициент ψ =1,79.

Момент инерции балки относительно вертикальной оси равен

J=0,8³·90/12+2·18³·1/12=976 см⁴.

Коэффициент φ находим по формуле (9.25): φ = 1,79(976/123132)∙ ∙(92/270)²·10³ = 1,64.

Коэффициент φ >1,55. Это значит, что при расчете можно принять φ=1. Устойчивость балки при наличии закреплений на расстоянии l_о = 2,7 м обес­печена.

Чтобы обеспечить устойчивость вертикального листа, следует приварить к нему ребра жесткости. Зададимся расстоянием между ними а= l,5h_B = 1,35 м. В этом случае следует знать следующие величины:

1.Нормальное напряжение в верхнем волокне вертикального листа. Оно было определено раньше: σ₁= 157,2 МПа.

2.Среднее касательное напряжение τ от поперечной силы. В середине пролета Q = 43,7 кН; среднее напряжение τ =Q/( h_B ·s_B)= =0,0437/(0,9·0,8·10-²)=6,06 МПа.

3. Местное напряжение σ_м под сосредоточенной силой (рис. 9.10 г). Это напряжение находим по формуле (9.22), принимая m=1:

σ_м = P/( s_B z).

Для определения z по формуле (9.23) подсчитаем J_п - момент инерции верхне­го пояса с приваренным к нему рельсом. Примем сечение рельса 50x50 мм (рис. 9.10 д). Ордината центра тяжести сечения пояса и рельса относительно верхней кромки пояса равна

y= (-18·1·0,5+5·5·2,5) /(18·1+5·5) = 1,2 см.

Положительное значение указывает на то, что центр тяжести расположен выше верхней кромки пояса.

Определим сначала момент инерции относительно оси, совпадающей с верх­ней кромкой пояса (эта ось параллельна центральной оси):

J_п =5³·5/3+1³·18/3 = 214,3 см⁴.

Теперь найдем момент инерции относительно оси х₀, проходящей через центр тяжести сечения пояса с рельсом (F = 43 см²):

J_п = J΄_п -F·y²= 214,3 – 43·1,2²=152,4 см⁴.

Вычислим условную длину по формуле:

z=3,25 ³√152,4/0,8= 18,7 см.

Из формулы (9.22) находим σ_м от Р=50 кН:

σ_м =0,05 · 1 /(0,008·0,187)=33,4 МПа.

Для проверки правильности постановки ребер жесткости (рис. 9.10, e) надлежит выяснить три вспомогательные величины:

1) σ_о по формуле (9.33):

σ_о = 75·10³·0,8·10^-3/0,9 = 667 МПа;

2) τ_о по формуле (10.34), где u=a/h_B=1,5; d=h_B=90 см.

Отсюда

τ_о =(125+95/1,5²) (100·0,008/0,9)²= 132,1 МПа;

3) σ_м0 по формуле σм₀= К₁(s_в/α)²10⁶. (9.47)

Для определения К₁ воспользуемся зависимостью

При a/h_B = 1,5 К₁=8,6, поэтому

σ_м0=8,6·10⁶ (0,8/135) ²=302,1 МПа.

Проверим по формуле (9.31), обеспечена ли требуемая устойчивость. Для этого подставим найденные значения в эту формулу:

√ (157,2/667,0 +33,4/302,1)² + (6,06/132,1)² = 0,35< 1.

Устойчивость вертикального листа в середине пролета вполне обеспечена. Посмотрим, обеспечена ли устойчивость в опорных сечениях. На опоре σ₁ = 0

τ=Q/( h_B s_b)=0,11375/(0,9·0,008) = 15,8 МПа.

Проверяем снова устойчивость для опорного сечения, полагая σ = 0:

√ (33,4/ 302,1 )²+ (15,8/132,1)² = 0,12.

Таким образом, устойчивость в опорном сечении обеспечена еще лучше, чем в середине пролета.

Переходим к расчету поясных швов. Катеты верхних и нижних поясных швов примем равными K=6 мм. В нижних поясных швах действуют касатель­ные напряжения, равные τ= QS/(0,7·2JK),

где Q=113,75H; S=18·1 ·45,5 = 819 см³; J=123 132 см⁴.

Отсюда τ = 0,11375 ·819·10^-6/(0,00123132 ·2 · 0,7·0,006)=9,2 МПа.

Несмотря на то, что рабочие напряжения незначительны, по технологиче­ским соображениям целесообразно оставить K=6 мм.

В верхних поясных швах при определении напряжений следует вычислять S с учетом приваренного рельса:

S=18·l ·45,5+5·5·48,5=2031 см³.

Момент инерции будем считать неизменившимся, как и положение центра тяжести балки. При этом

τ =0,11375·2031 · 10^-6/(0,00123132·2·0,7·0,006) =22,8 МПа.

В верхних поясных швах к вычисленным напряжениям добавляются τ_Р от сосредоточенной силы Р. Как уже было установлено, длина зоны распреде­ления сосредоточенной силы в вертикальном листе z =18,7 см (рис. 9.10 г).

Таким образом, по формуле (9.34) местное напряжение в шве (n= 0,4) при K=6 мм

τ _р=0,4·0,05/(0,187·2·0,7·0,006) = 12,7 МПа.

Условное результирующее напряжение по формуле (9.35)

τ_рез= 26,1 МПа.

Допускаемое напряжение в поясных швах определим из соотношения

[τ']=0,65[σ]_р=104 МПа.

Катеты швов, приваривающих ребра жесткости к поясам и стенкам, прини­маем такими же, как и поясных швов, т. е. К = 6 мм. Эти швы не передают рабочих напряжений и расчету на прочность не подлежат.