Поиск оптимального решения по векторному критерию
Пусть А=(а1, а2,…, аm,….) – множество реализуемых альтернатив, где каждая альтернатива соответствует конкретному значению вектора xÎX, т.е. аi=а(хi). Это множество может быть конечным (все альтернативы могут быть заранее известны или перечислены) и бесконечным.
Под оптимальной будем понимать альтернативу, обеспечивающую наилучшее (максимальное) значение векторного критерия эффективности W = W( а(x)). Тогда оптимальная альтернатива запишется в виде
а 0(x0) = max { W(a(x)) },
где W(a(x)) - значение векторного критерия при альтернативе a(x).
К сожалению, решения x0, обеспечивающего максимального значения по каждой компоненте векторного решения одновременно, как правило, не существует. Поэтому решения ищут среди эффективных или Паретовских (xÎXп )
ОПТИМАЛЬНОСТЬ ПО ПАРЕТО.
Прежде чем рассматривать данный метод, определим понятие доминирования
Альтернатива А1 доминирует над альтернативой А2, если по всем показателям (локальным критериям Wi) А1 не уступает А2, а хотя бы по одному из них лучше.
Данный метод, рассматривая все множество альтернатив, отбрасывает те из них, которые доминируются хотя бы одной альтернативой. Таким образом, создается множество недоминируемых альтернатив. Такое множество называется Парето оптимальным, и именно из него следует выбирать решение. Поиск решений по принципу Парето-оптимальности дает, в общем случае, множество допустимых решений, а не одно единственное.
Если множество X (и, соответственно, множество альтернатив) бесконечно или велико, и прямой перебор невозможен, то целесообразно выработать некоторое правило, по которому можно осуществлять целенаправленный поиск только, по крайней мере, части точек xÎXп (например, переходя от непрерывного множества значений x к дискретному с некоторым шагом Dx), исключая при этом из рассмотрения заведомо неперспективные точки.
Для выбора наилучшего решения среди множества найденных xÎXп можно привлечь дополнительную неформальную информацию о ценности вариантов решений, составляющих Парето-оптимальное множество. Держателем такой информации обычно является лицо, принимающее решения (ЛПР). Именно ЛПР, рассматривая и анализируя недоминируемые альтернативы, выбирает ту из них, которая с его точки зрения является оптимальной (точнее рациональной).
На критериальной плоскости, для случая двухкомпонентного векторного критерия, оптимальными по Парето решению будут (см. рис.)
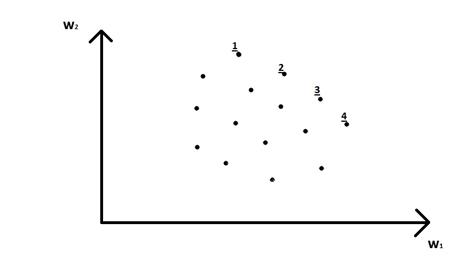
Альтернатива 1,2,3,4 – Оптимальные по Парето.
Остальные доминируемые.
Дата добавления: 2018-03-01; просмотров: 632;
