ПО СКАЛЯРНОМУ (СВЕРНУТОМУ) КРИТЕРИЮ
В дальнейшем, не снижая общности, будем обозначать сверткувекторного критерия в скаляр как U=U(Wn)=U(w1,w2...wn).
В этом случае, под наилучшим будем понимать решение, обеспечивающее максимальное значение обобщенного показателя U=U(Wn). Тогда задача поиска оптимального решения может быть записана следующим образом:
Необходимо найти такое решение x = x° (xÎX),которое обращает показатель обобщенный показатель эффективности операции U в максимум
U° (x°) = мах U(Wn(x))
XÎX
Принципиальным отличием данной задачи от традиционных задач математического программирования является то, что значение целевой функции U(x)вычисляется не напрямую, а через модель исследуемой системы W = W(x)и функцию свертки U= U(Wn), т.е. U(Wn(x)). Это приводит к тому, что вид целевой функции (выпуклая, монотонная, многоэкстремальная), как и области решения по оптимизируемым переменным Х (выпуклая, невыпуклая) априорно неизвестен. Поэтому для поиска экстремума необходимо использовать численные методы оптимизации, допускающие решение задачи в широком классе целевых функций и ограничений.
МЕТОД «ВЗВЕШЕННОЙ СУММЫ»
B этом случае обобщенный показатель U представляется в виде суммы показателей с весовыми коэффициентами ai, которые отражают ценность i-ого показателя (его важность для обобщенного показателя) по сравнению с остальными.
n
U =å ai ui
i=1
Весовые коэффициенты ai представляют в этом случае компоненты вектора градиента целевой функции. Поиск решения сводится к задаче оптимизации с целевой функцией, линейной относительно компонент векторного критерия Wn(w1,w2...wn), но не вектора Х. Наилучшим будет решение, расположенное максимально далеко в критериальном пространстве от начала координат в направлении градиента (см. рис.).
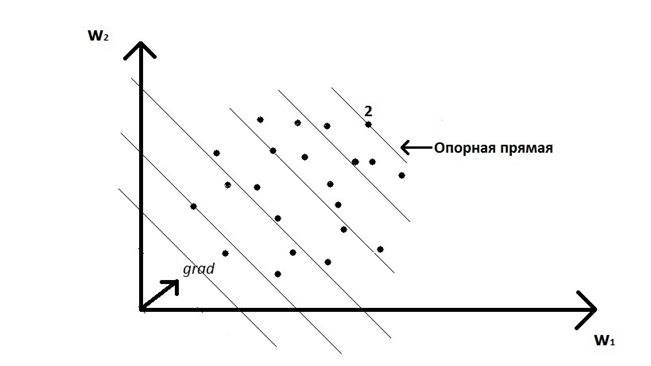
Альтернатива 2 оптимальна по взвешенной сумме
МЕТОД ИДЕАЛЬНОЙ ТОЧКИ.
В этом случае обобщенный показатель U=U(Wn)=U(w1,w2...wn)вычисляется как расстояние (длина вектора) в критериальном пространстве между точкой с текущими координатамиWn=U(w1,w2...wn)и точкой (идеальной), координаты которой задаются ЛПР (экспертом) Wnид =U(w1ид,w2ид...wnид).Как правило, такое решение (идеальное), в общем случае может не существовать, т.е. не реализуемо.
Значение целевой функции U(x)вычисляется также не напрямую, а через модель исследуемой системы и функцию свертки, т.е. U(Wn(x)).
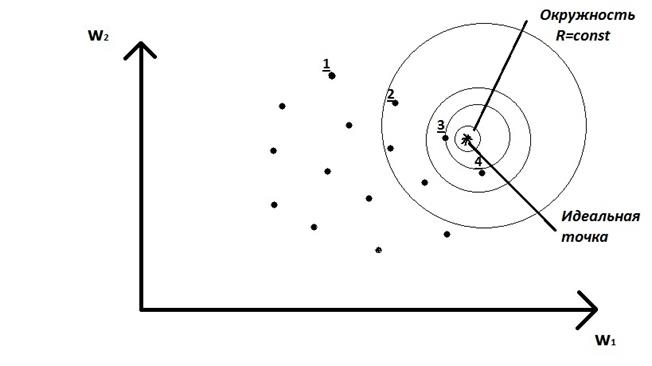
Альтернатива 3, ближайшая по расстоянию до идеальной точки
ПОИСК ПО ПОЛЕЗНОСТИ (ПРЕДПОЧТЕНИЯМ)
Полезность часто задаётся ЛПР (или экспертом) в виде функции полезности – некоторой функции вида U=F (Wn)= F (w1,w2...wn),отражающей «полезность» получаемых решений с его точки зрения (формализованная свертка). Вид функции полезности обычно выбирается из заданного класса функций в евклидовом пространстве.
Как было сказано выше, полезность может быть задана в критериальном пространстве в виде функции полезности (ФП) U=F (Wn)= F (w1,w2...wn),отражающей «полезность» получаемых решений с точки зрения ЛПР.
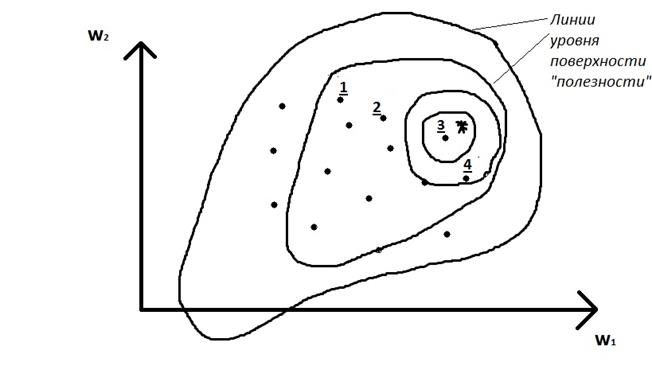
Альтернатива 3, наилучшая по полезности
Аналогично и предпочтения также являются индивидуальной оценкой качества альтернатив, определяемой ЛПР и отображают его систему ценностей (предпочтений) на множестве альтернатив.
Для задания предпочтений (в отличие от полезности) используется качественная (лексическая) шкала, на которой значения задаются в виде некоторых высказываний (термов), упорядоченных по предпочтению в порядке возрастания (убывания).
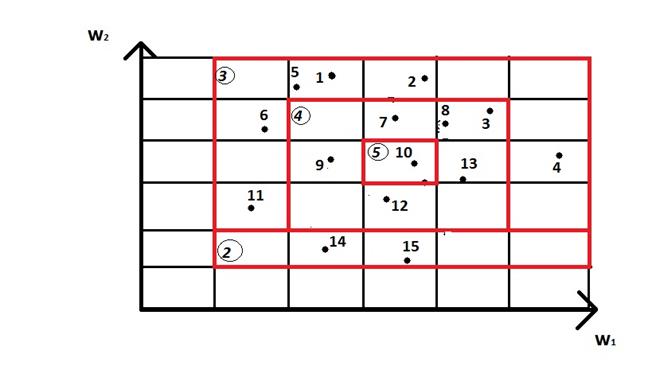
1-недопустимо
2-плохо
3-удвлетворительно
4-хорошо
5-отлично
Т.т. 14,15-«плохо»
Т.т.1,2,4,5,6,11-«удвлетворительно»
Т.т.7,8,3,9,12,13-«хорошо»
Т.10-«отлично»
Следует заметить, что при использовании методов, связанных с сопоставлением различных альтернатив по какой-либо компоненте векторного критерия понятие лучше (больше), в общем случае, не является монотонной функцией своего аргумента (напр. Температура воды для плавания в бассейне).
Дата добавления: 2018-03-01; просмотров: 559;
