Задачи и методы нелинейного программирования.

Задачи нелинейного программирования на практики встречаются весьма часто. Это связано с тем, что значения критерия эффективности связано со значениями переменных, как правило, сложной функциональной зависимостью и не всегда меняются линейно при изменении переменных.

Напр. Затраты выпуск продукции растут не пропорционально объему выпуска, т.к. при постоянных накладных расходах себестоимость единицы продукции падает при увеличении объема выпуска. Кроме того ограничения не ресурсы, связаны с возможностями по их поставкам и т.д.

Напр.

Предприятие планирует выпуск изделий двух наименований U₁ и U₂. Объем выпуска изделий каждого наименования x₁ и x₂ в условных единицах (напр. в тыс. штук) и ограничивается сверху необходимым ресурсным обеспечением, задаваемыми ограничением:

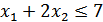
и ограничением, обусловленным имеющимися производственными мощностями заданными в виде

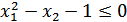
Прибыль от выпуска продукции растет пропорционально объему выпуска (2x₁ + x₂ ) за счет ее продажи и уменьшается пропорционально квадрату объема выпуска из-за необходимости проведения дополнительных операций по складированию и их оплате. Записывается в виде:

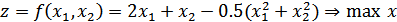
При ограничениях:

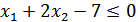(1)

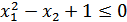(2)

;

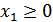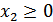
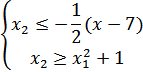
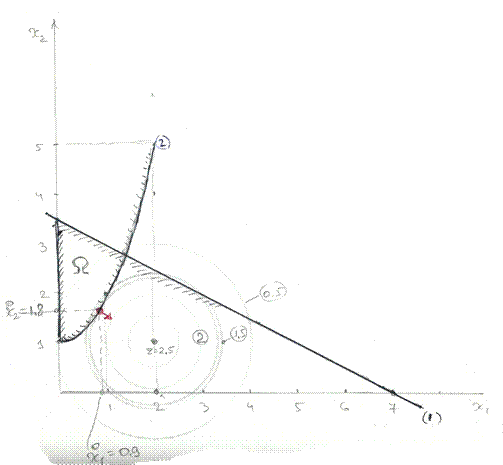
Графически задача может быть представлена в следующем виде на плоскости X₁0X₂

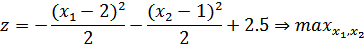
Здесь 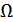– область определения X. Линия уровня целевой функции – замкнутые кривые –окружности с центром в т. (2,1). Z(2,1) = 2.5

По мере удаления о т центра R=0 значения функции Z падают.

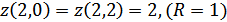
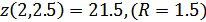
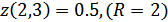
Оптимальное решение:

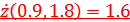
В общем случае задача нелинейного программирования записывается в следующей постановке:

Необходимо найти неотрицательные значения переменных x₁, x₂…, x_n, обращающих в максимум (минимум) целевую функцию вида

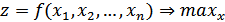
при ограничениях на переменные:

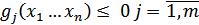
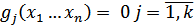
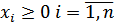
Общих способов решения ЗНП не существует. В каждом конкретном случае он выбирается исходя из вида целевой функции и ограничений, задающих область определения X целевой функции.

Задачи подобного рода возникают как в теории управления, экономике, так и в естественных науках. Систематическое их исследование, начатое в конце 40-ых годов привело к возникновению самостоятельной научной дисциплины – нелинейного программирования.

Классические способы поиска оптимального решения основаны на нахождении значений аргументов 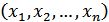, обращающих в ноль первые частные производные целевой функции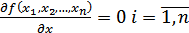

в случае отсутствия ограничения на переменных (безусловный экстремум.)

Если в задаче присутствуют только ограничения в виде равенства, то она может быть сведена к решению задачи без ограничений введением дополнительных переменных – множителей Лагранжа и поиску безусловного экстремума для ф-и Лагранжа вида:

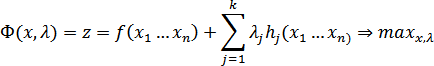
Однако в этом случае, как видим, размерность задачи увеличивается, что приводит к необходимости решений (n+k) уравнений, приравнивающих к нулю первые частные производные функции Лагранжа по 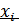и .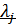

Найденные т.о. решения (если их несколько) проверяются на выполнение ограничений 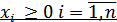и неподходящие отбрасываются.

Затем ищутся решения, лежащие на поверхности n-мерного гиперкуба 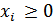, удовлетворяющие ограничениям 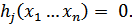Для этого к ограничениям 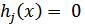дополнительно вводятся поочерёдно ограничения равенства нулю переменных 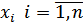в различных комбинация по одной 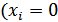), по двум 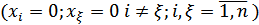и т.д. до тех пор, пока общее число ограничения будет не больше числа переменных n.

После того, как будут найдены все решения, удовлетворяющие системе ограничений 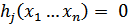; 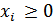они сравниваются между собой и среди них выбирается наилучшее (глобальный ext).

В найденном решении часть множителей Лагранжа 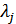могут быть равные 0. Это означает, что соответствующее ограничение 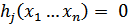является несущественным, т.е. не влияет на решение задачи и без ущерба для нее может быть исключено из дальнейшего рассмотрения.

Метод множителей Лагранжа может быть распространен и на решение задачи с ограничениями в виде неравенств

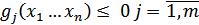
В этом случае для каждого неравенства вводится дополнительная переменная 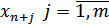и ограничение преобразуется к равенству

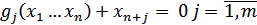
и задача сводится к предыдущей.

Условия существования оптимального решения вытекает из теорем Куна-Таккера, которые сводятся к тому, что для дифференцируемой в т. 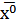функции 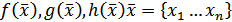линейная комбинация градиентов целевой функции 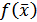,и функции 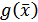,задающие активные ограничения в виде неравенств и функции 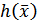,задающей ограничение в виде равенств в точке 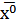должна обращаться в ноль.

Как видно из сказанного решение ЗНП классическим методом сводится к необходимости многократного решения систем уравнений равенства нулю частичных производных ф-м Лагранжа, что 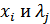, что сама по себе представляет значительные вычислительные трудности. Кроме того сами функции 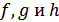не всегда задаются аналитическими, что не позволяет найти частные производные.

Поэтому наряду с классическими способами поиска 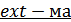широкое применение нашли различные виды численных методов оптимизации.