Метод крутого восхождения (наискорейшего спуска).

В основе метода крутого восхождения лежат следующие правила:

1. В качестве вектора возможных направлений выбирается вектор градиента целевой функции 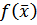, т.е.

=

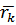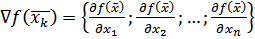
2.Величина шага 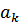определяется

- либо из условия ,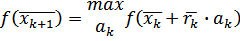

- либо задается фиксировано;

- либо изменяется по определенному правилу (увеличивается, либо уменьшается)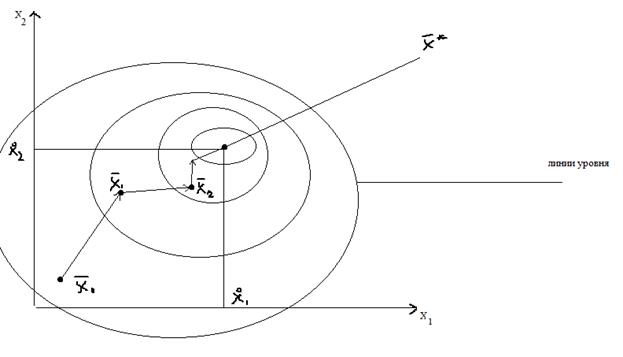

В указанном виде метод используется только тогда, когда отсутствуют ограничения на переменные. Если функция 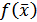выпуклая, то метод сходится к 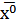, причем скорость сходимости зависти от выбора начальной точки 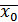и величины заданного шага.

Если целевая функция невыпуклая, то существует несколько точек экстремума функции и метод из разных начальных точек может сходиться к разным локальным экстремальным точкам.

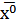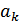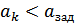В качестве критерия остановки(близости к ) обычно используют : либо величину шага (если , то останов), либо приращение целевой функци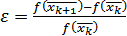и (если 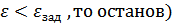, либо максимальное число шагов 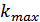, либо их все в совокупности. Все эти способы оценки сходимости к оптимальному решению имеют свои недостатки и не позволяют полностью оценить близость найденного решения к оптимальному.