Применение других видов средних величин

1. Средняя квадратическая равна корню квадратному из средней арифметической квадратов значений признака:

.

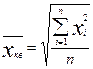Данный вид средней используется, если при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Квадратическая средняя применяется для измерения вариации в совокупности.

2. Средняя геометрическая:

.

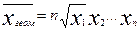Геометрическую среднюю надо применять, если при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин. Основное применение этот вид средних находит при определении средних темпов роста.

3. Средняя гармоническая:

.

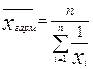Данный вид средней применяют, если необходимо, чтобы при осреднении неизменной оставалась сумма величин, обратных индивидуальным значениям признака. Эта формула применяется в задачах о средних ценах, средней скорости движения транспорта и других.

Соотношение между средними: чем выше показатель степени средней, тем больше значение средней величины (если индивидуальные значения варьируют). Имеем соотношение, называемое правилом мажорантности средних:

Х гарм < Х геом < Х арифм < Х куб.