Средняя арифметическая величина.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

Средняя арифметическая величина – “среднее слагаемое». При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Например, средняя заработная плата или средний доход работников предприятия - это такая сумма денег, которая приходилась бы на каждого работника, если бы весь фонд оплаты труда (или все доходы, направленные на личное потребление) был распределен между работниками поровну.

Исходя из определения, формула средней арифметической величины (простой) имеет вид:

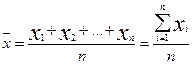, где n – численность совокупности. (1)

По формуле (1) вычисляются средние величины первичных (объемных) признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, как, например, табл.:

Общее число забитых мячей, согласно исходной информации таблице, можно получить как сумму произведений значений признака в каждой группе х_i на число игр с таким количеством забитых мячей f_i (частоты).

Получим формулу (2):

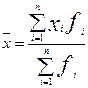, где n – число групп. (2)

Такую форму средней арифметической величины называют взвешенной арифметической средней. В качестве весов выступают здесь числа единиц совокупности в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины.

Средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения (дискретный признак).