Тема 5.4. Структурные характеристики вариационного ряда распределения.
Такими показателями являются медиана, мода распределения и другие показатели.
Медиана распределения
Медиана - величина варьирующего признака, делящая совокупность на две равные части - со значениями признака меньше медианы и со значениями признака больше медианы. Рассмотрим пример.
Таблица 1
Крупные банки Санкт-Петербурга на 01.07.96
| Название банка | Собственный капитал, млрд. руб. |
| Агропромбанк | |
| Петровский | |
| Балтийский | |
| Банк Санкт-Петербург | |
| Промстройбанк |
Рассчитаем среднюю величину и медиану.
Средняя (по Xар) = 269 млрд. руб.
Медиана (Ме) = 196 млрд. руб.
На примере видно принципиальное различие между медианой и средней величиной. Медиана не зависит от значений признака на краях ранжированного ряда. Если бы даже капитал крупнейшего банка Санкт-Петербурга был вдесятеро больше, величина медианы не изменилась бы. Поэтому если ряд значений неоднороден, включает резкие отклонения от средней, медиану используют как более надежный показатель типичного значения признака, вместо арифметической средней. В данном ряду средняя величина собственного капитала, равная 269 млрд руб., сложилась под большим влиянием наибольшей варианты, 80% банков имеют капитал меньше среднего и лишь 20% - больше. Вряд ли такую среднюю можно считать типичной величиной.
При четном числе единиц совокупности за медиану принимают арифметическую среднюю величину из двух центральных вариант, например при десяти значениях признака - среднюю из пятого и шестого значений в ранжированном ряду.
В интервальном вариационном ряду медиана рассчитывается по формуле:
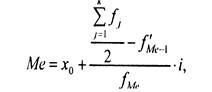
где x0 - нижняя граница интервала, в котором находится медиана;
f’Ме-1 - накопленная частота в интервале, предшествующем медианному;
fМе - частота в медианном интервале;
i - величина медианного интервала; k - число групп.
Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные по числу единиц части. Эти величины называются квартилями и обозначаются Q1, Q2, Q3, Q4.
Значения признака, делящие ряд на пять равных частей, называют квинтилями, на десять частей – децилями и другие.
Мода распределения
Мода – это значение признака, которое встречается в изучаемом ряду чаще всего.
В дискретном ряду мода определяется без вычисления как значение признака с наибольшей частотой. Например, по данным таблицы о числе забитых мячей из лекции о средних величинах модой является число 2, т.е. чаще всего (71 раз) за футбольные матчи было забито по 2 мяча.
Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но с наибольшей частотой) значений признака имеются в вариационном ряду, он считается соответственно бимодальным либо мультимодальным (см. таблицу о числе членов семьи, тема - группировки). Это говорит о неоднородности совокупности.
В интервальном вариационном ряду модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала значение моды находят условно, по формуле:
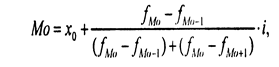
где xо - нижняя граница модального интервала;
fMo - частота в модальном интервале;
fMo-1 - частота в предыдущем интервале;
fMo+1 - частота в следующем интервале за модальным;
i - величина интервала.
Для однородной совокупности справедливо равенство:
Mo – x = 3[Me – x].
Контрольные вопросы
1. В чем различие моды и медианы?
2. Что называется модой?
3. Как рассчитывается медиана?
Дата добавления: 2017-12-05; просмотров: 974;
