Тема 9.2. Корреляционно-регрессионный анализ.

1. Статистическая оценка надежности параметров парной линейной корреляции.

2. Непараметрические показатели связи.

3. Уравнение регрессии.

4. Корреляционно-регрессионные модели.

1.Статистическая оценка надежности параметров парной корреляции

Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками статистической закономерности изучаемого процесса. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью понимается вероятность того, что значение проверяемого параметра не равно нулю.

Надежность линейного коэффициента корреляции (r) проверяется с использованием t-критерия Стьюдента:

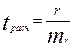, где m_r - средняя случайная ошибка коэффициента корреляции.

Средняя случайная ошибка коэффициента корреляции:

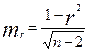, где n - число наблюдений.

Расчетный t-критерий необходимо сравнить с табличным значением (t_табл) при выбранном вами уровне значимости (0,01, 0,05, 0,1).

Если t_расч > t_табл, то коэффициент линейной корреляции достоверен с определенной вероятностью.

Если t_расч < t_табл, то говорят: "связь надежно не установлена".

2.Непараметрические показатели связи

1. Коэффициент Фехнера:

Кф = (С-Н) / n,

Где С, Н - число наблюдений, у которых по паре признаков X и Y наблюдается совпадение (С) или несовпадение (Н) знаков отклонения от средних уровней.

Кф показывает наличие и направление связи. Если Кф>0, то связь прямая, ели Кф<0, то связь обратная.

2. Коэффициент корреляции рангов.

2.1. по формуле Спирмена (для линейной зависимости):

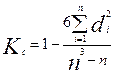, где d_i = ранг(х_i) - ранг(y_i).

Порядок расчета Кс:

1) проранжировать значения X и Y в одном и том же порядке (либо по возрастающей, либо по убывающей);

2) найти разности рангов d_i ;

3) получить результат по формуле.

2.2. по формуле Кэндалла (для нелинейной зависимости):

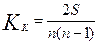, где S - фактическая сумма рангов.

Если у нескольких единиц наблюдения величина признака будет одинаковой, то их нумеруют подряд и присваивают среднее из этих рангов.

3. Уравнение регрессии

Уравнение регрессии может быть парным или множественным. Если изучается влияние одного фактора на результативный признак, то получают уравнение парной регрессии. При изучении влияния множества факторов на результативный признак получают уравнение множественной регрессии.

Регрессия бывает линейной (выражается уравнением прямой) или криволинейной (выражается уравнениями параболы, гиперболы и т.д.).

Линейная регрессия применяется чаще всего.

Уравнение парной линейной регрессии: У = а + bх

Уравнение множественной регрессии: У = а + b₁х₁ + b₂х₂ + … + b_nx_n.

Где у – теоретическое (расчетное) значение результативного признака,

а_, b_1, b₂…b_n – параметры уравнения регрессии,

b_1, b₂…b_n – коэффициенты чистой регрессии.

Коэффициенты чистой регрессии измеряют среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения. Коэффициенты регрессии выражаются в тех же единицах измерения, что и признаки-факторы. Параметр а показывает остаточное влияние факторов, не включенных в уравнение регрессии. Переменные х_1, х_2, x_n.- значения факторного признака.

Для того, чтобы правильно выбрать форму уравнения регрессии необходимо:

1. Изобразить графически изучаемое распределение Х и У (т.е. построить корреляционное поле).- рисунок.

2. Путем перебора различных видов уравнений, выбрать тот вид уравнения регрессии, для которого сумма квадратов отклонений фактических значений от теоретических минимальна: ∑(у_i – ў)² → min.

3. Оценить надежность полученного уравнения.

Метод наименьших квадратов

Параметры уравнения регрессии определяются с помощью метода наименьших квадратов (МНК). МНК заключается в решении системы нормальных уравнений. Число уравнений в системе зависит от числа параметров уравнения регрессии. Для линейной регрессии:

an + b∑x = ∑y

a∑x + b∑x² = ∑yx

Необходимо определить a и b.

Определяем сначала а, затем подставляем в другое уравнение и выражем b.

Оценку правильности выбора вида уравнения регрессии и характеристику значимости всего уравнения получают с помощью F-критерия Фишера, который представляет собой отношение большей дисперсии к меньшей, рассчитанных на одну степень свободы, или по формуле:

F_расч = [R2(n-m)] / [(1-R²)(m-1)], где

n - число наблюдений, m - число параметров уравнения регрессии.

Если Fрасч > Fтабл, то вид уравнения выбран верно.

Если Fрасч < Fтабл, то следует пересмотреть форму уравнения, перечень переменных и т.д.

Оценку значимости параметров уравнения регрессии проводят также, как для коэффициента линейной корреляции (с помощью t-критерия Стьюдента).

Экстраполяция регрессионных уравнений - расчет ожидаемых (прогнозируемых) значений результативного признака.

4.Корреляционно-регрессионные модели

Корреляционно-регрессионные модель - аналитическая форма множественной или парной корреляции.

Корреляционно-регрессионной моделью считается такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного фактора, обладает высоким (не ниже 0,5) коэффициентом детерминации и статистически значимыми и экономически обоснованными коэффициентами регрессии.

Рекомендации для построения корреляционно-регрессионной модели

1. Признаки-факторы должны находиться в причинной связи с результативным признаком. Поэтому, недопустимо, например, в модель себестоимости вводить в качестве одного из факторов коэффициент рентабельности, хотя включение такого фактора значительно повышает коэффициент детерминации.

2. Признаки-факторы не должны быть составными частями результативного признака или его функциями (в этом случае коэффициент корреляции равен единице). Например, при анализе производительности труда в промышленности нельзя как признак-фактор использовать индексы физического объема промышленной продукции, так как они входят в формулу для расчета производительности труда.

3. Не рекомендуется включать в уравнение факторы слабо связанные с результативным признаком, но тесно связанные между собой. Например, если r_yx1 = 0,55, r_yx2 = 0,67, r_x1x2 = 0,88, то в регрессионное уравнение следует включить фактор x2, а фактор x1 не включать, так как он тесно связан с x2, и его корреляция с y слабее, чем корреляция x2.

4. Нельзя включать в модель факторы разных уровней иерархии, т. е. фактор ближайшего порядка и его субфакторы. Например, в моделях себестоимости зерна не следует включать и урожайность зерновых культур, и дозу удобрений под них или затраты на обработку гектара, показатели качества семян, плодородия почвы, т. е. субфакторы самой урожайности.

5. Необязательное, но желательное условие, чтобы между результативным и факторными признаками соблюдалось единство единицы совокупности, к которой они отнесены. Т.е. если результативный признак рассчитан в целом по области, то все факторы также должны относиться к областному уровню. Однако, при анализе влияния факторов на розничный товарооборот области допустимо рассматривать фактор задолженности по заработной плате в промышленности. Так, размер среднемесячной начисленной зарплаты в промышленности Оренбургской области в среднем в два раза больше среднемесячной начисленной зарплаты в целом по области. Невыплата зарплаты на промышленных предприятиях отражается на величине розничного товарооборота.

6. При выборе между двумя корреляционно-регрессионными моделями предпочтительнее модель с меньшим числом факторов при том же коэффициенте детерминации или даже при несущественно меньшем коэффициенте. Но величина коэффициента детерминации в полученной модели должна быть не менее 0,5.

Для изучения множественной корреляции и отбора факторов в модель используется матрица парных коэффициентов корреляции. При этом необходимо иметь в виду, что в экономических исследованиях часто проявляется эффект взаимодействия (взаимозаменяемости) факторов, т.е. мультиколлинеарность (или по двум факторам - коллинеарность). Поэтому факторы, имеющие r>0,8 в модель не включаются (см. п. 3 Рекомендаций построения КРМ).

Чаще всего уравнение множественной регрессии имеет линейную форму.

У = а + b₁х₁ + b₂х₂ + … + b_nx_n = а + ∑b_jх_j, где

j - число факторных признаков.

Так как коэффициенты чистой регрессии выражаются в тех же единицах измерения, что и признаки-факторы, невозможно узнать, какой же фактор сильнее воздействует на результат. Поэтому необходимо коэффициенты чистой регрессии выразить в стандартизированной форме: в виде β-коэффициентов и коэффициентов эластичности (Э).

Расчет β-коэффициентов:

β₁ = b₁* 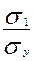; β₂ = b₂* ; …

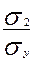β-коэффициент показывает, на сколько средних квадратических отклонений изменится в среднем результативный признак, если соответствующий фактор изменится на свое среднее квадратическое отклонение.

Расчет коэффициентов эластичности:

Э₁ = b₁* 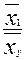; Э₂ = b₁* ; …

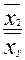Коэффициентов эластичности показывает, на сколько процентов изменится в среднем результативный признак, если фактор изменится на один процент.

Соотношение между β_i и Э_i: β_i /Э_i = vx_i / vy.

β-коэффициенты всегда меньше коэффициентов эластичности.

Контрольные вопросы

1. Что называется корреляционно-регрессионным анализом?

2. Напишите уравнение нелинейной корреляционной связи.

3. Напишите уравнение прямолинейной корреляционной связи

Рекомендуемая литература

Основная

1. Мхитаряна. В.С., Дуброва Т.А., Минашкин В.Г. Статистика: Учебник - 2-е изд., стер. - Москва: Издательский центр «Академия», 2003г. – 272с.

2. Профессора Р.А. Шмойловой. Теория статистики: Учебник. – Москва: Финансы и статистика, 2000г.

Дополнительная

1. В.Г. Ионина. Статистика: Учебник.– Новосибирск, изд. НГАЭиУ, 2000

2. Сиденко А.В., Попов Г.Ю., Матвеева В.М., Статистика: Учебник – Москва: Дело и Сервис, 2000г.

3. Шмойловой. Р.А., Практикум по теории статистики: Учебник. - Москва: Финансы и статистика, 2000г.

Электронные Интернет-ресурсы

Годин А.М. Статистика: Учебник [Электронный ресурс] URL: http://www.knigafund.ru/