Статистические методы распознавания

Основная цель технической диагностики состоит в распознавании состояния объекта – то есть отнесение состояния объекта к одному из возможных классов (работоспособное, неработоспособное) на основе полученной диагностической информации.

Статистические методы распознавания имеют преимущество перед другими методами в возможности одновременного учета признаков различной физической природы, так как используют безразмерные величины – вероятность появления тех или иных признаков при различных видах технического состояния объекта.

Наиболее простым и эффективным статистическим методом распознавания является метод, основанный на формуле Байеса. Недостаток этого метода состоит в необходимости получения достаточного объема предварительной статистической информации, однако, для таких массовых видов интенсивно эксплуатируемых объектов, как вагон, этот метод вполне приемлем.

Если имеется диагноз (состояние объекта) D_i и признак k_j, встречающийся при этом диагнозе, то имеем вероятность совместного появления событий: наличие у объекта состояния D_i и признака k_j:

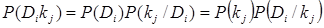, (1.14)

где P(D_ik_j) – вероятность логического произведения событий D_i и k_j;

P(k_j / D_i ) – условная вероятность: вероятность события k_j при условии, что произошло событие D_i;

P(D_i / k_j) – условная вероятность: вероятность события D_i при условии, что произошло событие k_j.

Нас интересует вероятность диагноза D_i при условии обнаружения признака k_j. Из формулы (1.14) имеем формулу Байеса:

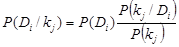, (1.15)

k_j может представлять комплекс признаков или интервалы параметров одного из признаков. Очевидно, что детерминистский метод распознавания является частным случаем вероятностного метода, когда P(D_i / k_j)=1.

Рассмотрим пример определения вероятности обнаружения неисправного подшипника по признаку перегрева его корпуса. Отказ буксового подшипника, как правило, сопровождается его перегревом. В условиях эксплуатации есть возможность на ходу поезда измерять уровень перегрева корпуса буксы, ориентируя на нее датчики инфракрасного излучения, как показано на рис. 1.12.

Обозначим: D₁ – исправное состояние подшипника; D₂ – неисправное состояние подшипника; признак k₁ – перегрев корпуса буксы в интервале от 30°C и выше.

Нас интересует вероятность того, что в буксовом подшипнике имеется дефект при условии обнаружения перегрева корпуса буксы свыше 30°C:

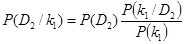, (1.16)

Пример: Имеем данные анализа обследования N_ij подшипников, первый индекс относится к диагнозу (1 – исправное состояние, 2 – дефект, 0 – все случаи), второй индекс относится к признаку (1 – наличие признака перегрева, 0 – все случаи).

Обследовано N₀₀=10000 подшипников, у которых предварительно измерялась температура перегрева корпуса буксы в эксплуатационных условиях. У N₂₀ = 20 подшипников обнаружены дефекты, из них N₂₁ = 18 подшипников имели перегрев корпуса свыше 30°C. Из всей выборки N₀₁=25 подшипников имели перегрев корпуса свыше 30°C.

По данным обследования определяем:

– вероятность наличия дефекта подшипника:

;

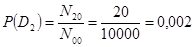– вероятность наличия признака перегрева корпуса буксы:

;

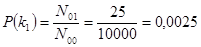– вероятность наличия признака перегрева корпуса буксы у дефектного подшипника:

;

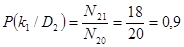– вероятность наличия признака перегрева корпуса буксы у исправных подшипников:

.

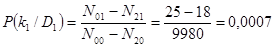Вероятность обнаружения дефектного подшипника:

.

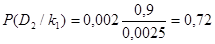Таким образом, мы убедились в том, что, имея сравнительно высокую вероятность наличия данного признака у неисправных подшипников P(k₁ / D₂ )= 0,9 и весьма малую вероятность наличия этого признака у исправных подшипников P(k₁ / D₁ )= 0,0007, вероятность обнаружения дефектного подшипника явно недостаточна P(D₂ / k₁)= 0,72.

Приведенный пример свидетельствует о необходимости корректировки порогового значения признака k₁ или применения дополнительных признаков. Тогда мы имеем комплекс признаков К, который включает n признаков k_j (k_1, k₂,… k_n), а каждый из признаков имеет m разрядов (k_j1, k_j2,… k_jm). В результате обследования узнаем реализацию признака k_j^*= k_js и всего комплекса признаков К^*. Для комплекса признаков можем написать обобщенную формулу Байеса:

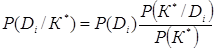. (1.17)

Вероятность появления комплекса признаков К^*:

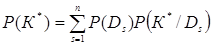, (1.18)

где n – количество возможных состояний (диагнозов) объекта.

Решающее правило в методе Байеса основано на введении порогового значения для вероятности диагноза:

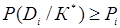, (1.19)

где P_i – заранее выбранный уровень распознавания для диагноза D_i. Обычно принимают .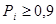

Поскольку статистический метод распознавания не дает возможности однозначного решения, то необходимо вводить некоторые условия оптимальности принятия решения.