Параметры технического состояния

Вагон, как объект технического диагностирования, обладает вполне определённой структурой, т.е. упорядоченной совокупностью совместно работающих элементов (деталей), образующих конструкцию и обеспечивающих выполнение заданных функций (взаимное расположение, форма и размеры взаимодействующих деталей, характер сопряжения, чистота их поверхности и др.).

Техническое состояние вагона можно охарактеризовать множеством количественных и качественных параметров. Структура вагона характеризуется структурными количественными параметрами, представляющими различные физические величины (размеры деталей, площади, объем кузова, тара, температура, напряжения и др.). Значения этих параметров могут быть начальными, допустимыми и предельными. Начальное значение структурного параметра характеризует техническое состояние вагона после его изготовления на заводе, при выпуске из капитального и деповского ремонта. В процессе эксплуатации структурные параметры изменяются, что приводит, к ухудшению технического состояния вагона (сборочной единицы). При дальнейшей эксплуатации вагона происходит накапливание изменений в деталях, сборочных единицах в таком количестве, что структурные параметры достигают предельного значения, соответствующего полной потере работоспособности сборочных единиц.

Для получения приближённой оценки состояния вагона выделяется совокупность прямых и косвенных признаков (диагностических параметров), отображающих наиболее вероятные дефекты, связанные со снижением работоспособности и возникновением отказов.

Под диагностическим параметром понимается параметр, изменение которого приводит либо к физическому отказу, либо к увеличению интенсивности процесса накопления повреждений в деталях вагона, т. е. параметр, обладающий наибольшей информативностью.

Структурная схема формирования процесса диагностирования, технического обслуживания и ремонта вагонов представлена на рис.1.14.

Разработка и создание системы технического диагностирования базируется на изучении сборочных единиц или деталей вагонов, их возможных отказов и включает в себя построение и анализ математических моделей, представляющих форматированное описание объекта в исправном состоянии в виде детерминируемых или вероятностных зависимостей между возможными воздействиями на объект и его реакциями на эти воздействия.

При построении математических моделей х обозначает m-мерный вектор, компонентами которого являются значения переменных величин на входе объекта, характеризующих воспринимаемые им воздействия х₁, х_{2 ,…,}х_m.

Аналогично у обозначает n-мерный вектор n параметров технического состояния или иначе внутренних структурных параметров у₁, у₂, …,у_n, а z обозначает r-мерный вектор значения r диагностических параметров на выходе объекта или иначе выходных функций z₁, z₂, …,z_r.

Запись

Z 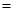(x, у_нач, t) , (1.45)

может обозначать аналитическую, векторную, табличную или другую форму представления системы передаточных функций исправного объекта диагностирования, отражающих зависимость реализуемых выходных функций z от входных переменных x , начального значения у_нач внутренних переменных и времени (наработки) t.

Система (1.45) является математической моделью исправного объекта. Можно выделить для рассмотрения конечное множество S возможных неисправностей объекта. При наличии в объекте неисправности SiES, i-1, 2,..,/ S / говорят, что он находится в i-неисправном состоянии или является i-неисправным. Объект, находящийся в i-неисправном состоянии, реализует систему передаточных функций:

Zi= i(x, у_нач,, t), (1.46)

предоставленных в той же форме, что и передаточные функции (1.45).

Система (1.46) для фиксированного i является математической моделью i-неисправного объекта.

Система (1.45) и совокупность систем (1.46) для всех SiES образует модель объекта диагностирования. Часто в явном виде задаётся только модель исправного объекта, т.е. зависимость (1.45), а поведение объекта в i-неисправных состояниях задаётся косвенно, через множество S возможных неисправностей (неявная модель объекта).

Показатели динамики изменения параметров деталей и сборочных единиц ПС в эксплуатации находят по результатам измерений и статистической обработки полученных данных. Отклонение значения структурного параметра (параметра состояния объекта) от номинала выражается случайной функцией:

S(t) = V_ct^α+в₁+z_i , (1.47)

где V_c – показатель случайной скорости отклонения параметра при наработке t=1, уменьшенной в α раз (ед. параметра/ед. наработки);

t – наработка (ч, км, ткм и т. д.);

α – показатель степени, характеризующий кривизну реализации на всём диапазоне измерений;

в₁ – показатель приработки детали (в ед. параметра);

z_i – стационарная случайная функция отклонения параметра с нулевым математическим ожиданием (в ед. параметра).

При выборе диагностических параметров деталей и сборочных единиц ПС в результате анализа статистических рядов значений структурных и диагностических параметров находят по каждому структурному параметру функцию его математического ожидания.

П=f(Пgj) (j=1, 2, …, к) , (1.48)

где П, Пgj – величины соответственно структурного и j-го диагностического параметров.

Затем с помощью критерия тесности связи – коэффициента r устанавливают корреляционную зависимость между j-м диагностическим параметром и структурным.

Диагностические параметры, для которых r мал, исключают.

Для остальных рассчитывают значения обобщающего показателя связи:

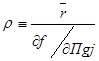
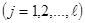, (1.49)

где 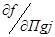– частная производная функции в точке, ордината которой равна допускаемому значению параметра;

ℓ – число оставшихся исследуемых диагностических параметров.

Большие значения обобщающего показателя связи служат в пользу выбора данного диагностического параметра.