Статистические методы выявления наличия корреляционной связи между
Признаками
Для ответа на вопрос, существует или нет корреляционная связь между двумя признаками, используют ряд специфических методов: параллельное сопоставление рядов, построение групповой и корреляционной таблиц, графическое изображение корреляционного поля.
Простейшим способом обнаружения связи является параллельное сопоставление двух рядов– ряда значений факторного признака и соответствующих ему значений результативного признака. Значения факторного признака 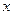 располагаются в возрастающем порядке, прослеживая тенденцию изменения соответствующих значений результативного признака
располагаются в возрастающем порядке, прослеживая тенденцию изменения соответствующих значений результативного признака 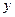 . В случае, когда возрастание величины факторного признака явно влечёт за собой рост величины результативного, говорят о возможном наличии прямой корреляционной связи. Если с увеличением
. В случае, когда возрастание величины факторного признака явно влечёт за собой рост величины результативного, говорят о возможном наличии прямой корреляционной связи. Если с увеличением 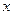 значение
значение 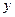 уменьшается, то можно предполагать обратную корреляционную связь между признаками.
уменьшается, то можно предполагать обратную корреляционную связь между признаками.
В качестве примера рассмотрим данные о выпуске продукции (результативный признак) и среднегодовой стоимости основных производственных фондов (факторный признак) по 20 предприятиям. В табл. 20 предприятия ранжированы по среднегодовой стоимости основных производственных фондов.
Табл.20.
| № предприятия | Среднегодовая стоимость основных производственных фондов, млн.руб. | Выпуск продукции, млн.руб. | № предприятия | Среднегодовая стоимость основных производственных фондов, млн.руб. | Выпуск продукции, млн.руб. |
В целом для всей совокупности предприятий можно видеть, что с увеличением стоимости основных производственных фондов увеличивается выпуск продукции. Это позволяет говорить о возможном наличии прямой корреляционной связи.
С помощью метода параллельного сопоставления двух рядов можно дать лишь самую общую характеристику связи, используя относительно небольшое имеющееся число наблюдений. Иногда наличие большого числа различных значений результативного признака, соответствующих одному и тому же значению признака-фактора, затрудняет восприятие параллельного сопоставления рядов. В таких случаях проводится построение корреляционной или групповой таблицы.
Рассмотрим построение корреляционной таблицына примере данных табл.20. Вначале проводится группировка значений факторного и результативного признаков: по формуле Стерджесса определяется число групп 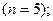 рассчитываются величины интервалов для факторного и результативного признаков (
рассчитываются величины интервалов для факторного и результативного признаков ( 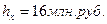 ,
, 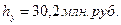 ); данные по количеству единиц совокупности, отвечающих определённому сочетанию значений признаков
); данные по количеству единиц совокупности, отвечающих определённому сочетанию значений признаков 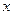 и
и 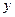 заносятся в корреляционную таблицу. В корреляционной таблице факторный признак
заносятся в корреляционную таблицу. В корреляционной таблице факторный признак 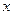 обычно располагают в строках, а результативный признак
обычно располагают в строках, а результативный признак 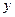 - в столбцах таблицы. Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного сочетания значений
- в столбцах таблицы. Числа, расположенные на пересечении строк и столбцов таблицы, означают частоту повторения данного сочетания значений 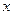 и
и 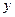 (табл.21).
(табл.21).
Табл.21.
Группы
(интервалы)
по 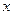
| Группы (интервалы) по 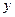
| ||||
| 59–89,2 | 89,2– 119,4 | 119,4-149,6 | 149,6-179,8 | 179,8-210 | |
| 40 – 56 | |||||
| 56 - 72 | |||||
| 72 - 88 | |||||
| 88 - 104 | |||||
| 104 - 120 |
Корреляционная таблица даёт возможность выдвинуть предположение о наличии или отсутствии связи, а также выяснить её направление. Если частоты в таблице расположены по диагонали из левого верхнего угла в правый нижний, то можно предположить наличие прямой корреляционной зависимости между признаками. Если же частоты расположены по диагонали из правого верхнего угла в левый нижний, то предполагают наличие обратной связи между признаками
При построении групповой таблицывсе наблюдения разбиваются на группы по факторному признаку, и по каждой группе вычисляют средние значения результативного признака. Групповая табл.22 построена по данным табл.20.
Табл.22.
| Группы предприятий по среднегодовой стоимости основных производственных фондов, млн.руб. | Среднее значение выпуска продукции, млн.руб. |
| 40 - 56 | |
| 56 - 72 | 114,3 |
| 72 - 88 | 129,7 |
| 88 - 104 | 129,3 |
| 104 - 120 |
В групповой таблице сравниваются средние групповые значения результативного признака. Если они увеличиваются с ростом признака-фактора, то можно предположить наличие прямой корреляционной зависимости.
Для предварительного выявления наличия связи и её характера применяют графический метод. Для этого на графике строят точки, соответствующие индивидуальным значениям признака-фактора и результативного признака. Совокупность полученных точек называют “полем корреляции”. Далее различными способами в пределах “поля корреляции” проводят график, интерпретирующий эмпирическую линию связи между факторным и результативным признаком. Если эмпирическая линия связи по своему виду приближается к прямой, то предполагается наличие линейной зависимости между признаками. Если же она по виду ближе к какой-либо кривой, то может предполагаться наличие соответствующей криволинейной связи между признаками.
Дата добавления: 2017-11-04; просмотров: 549;
