Описание взаимосвязей с помощью регрессионного анализа

Все явления и процессы, характеризующие социально-экономическое развитие и составляющие единую систему показателей экономики, тесно взаимосвязаны и взаимозависимы между собой. В статистике показатели, характеризующие эти явления, могут быть связаны корреляционными зависимостями различной степени тесноты, которые исследуются с помощью методов корреляционного и регрессивного анализов.

Корреляционный анализвзаимосвязи показателей позволяет решать следующие задачи:

1. Оценка тесноты связи между показателями с помощью парных и множественных коэффициентов корреляции.

2. Оценка уравнения регрессии.

Целью регрессионного анализаявляется получение оценки функциональной зависимости теоретического среднего значения результативного признака 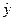от факторных 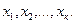При этом в регрессионном анализе заранее предполагается наличие причинно-следственных связей между результативным и факторными признаками.

Статистическая модель взаимосвязи явлений в виде уравнения регрессии

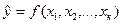
будет адекватно описывать реальное явление или процесс при выполнении следующих основных условий:

1) результативный признак должен подчиняться нормальному закону распределения относительно своих средних значений при различных значениях факторных признаков;

2) отдельные наблюдения, на основе которых строится модель регрессии, должны быть получены независимо друг от друга.

Одной из проблем построения уравнения регрессии является выбор её размерности – определение числа факторов, включаемых в модель. Число факторных признаков, входящих в модель должно быть оптимальным, т.е. необходимо учитывать существенные признаки и исключать несущественные (второстепенные) признаки.

Корреляционно-регрессионные модели, какими бы сложными они не были, не вскрывают полностью всех причинно-следственных связей, однако достаточно адекватно могут описывать влияние на результативные признаки существенных факторов, если проведён предварительный качественный анализ сущности и специфики исследуемых явлений и процессов.

В теории статистики изучаются парные и множественные корреляции. При парной корреляции рассматривается связь результативного признака с одним единственным факторным признаком, при множественной – с двумя и более факторными признаками. В соответствии с этим строящиеся регрессионные модели могут быть парные и множественные.

Например, если устанавливается зависимость уровня оплаты труда 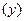от производительности труда 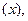то такая регрессия парная. Если же изучается зависимость уровня оплаты труда 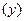не только от производительности труда 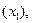но и от квалификации работников 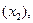цены продукции 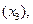качества продукции 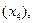то такая регрессия множественная.

Парная регрессия, характеризующая связь между результативным и факторным признаками, аналитически описывается уравнениями различного типа:

прямая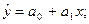

гипербола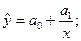

парабола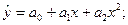

показательная функция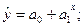

степенная функция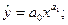

полулогарифмическая функция 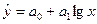и др.

Определить тип уравнения можно, используя различные способы, например, исследуя зависимость между признаками графически.

Оценка параметров 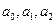уравнений регрессии осуществляется методом наименьших квадратов, сущность которого состоит в нахождении параметров 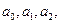при которых сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по уравнению регрессии, минимальна. Т.е.

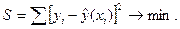
Распространенным случаем связи в общественных и экономических явлениях является прямая зависимость между результативным и факторным признаком. Для прямой зависимости

.

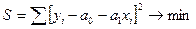Минимизируя 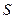как функцию параметров 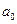и 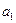, получаем систему уравнений:

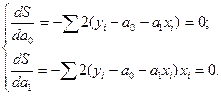
Преобразовав уравнения, получим систему обычных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов:

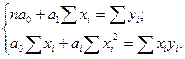
Решая систему этих уравнений, находим:

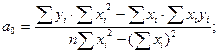
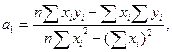
где 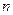- число единиц наблюдений (пар значений ).

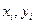Используя способ, аналогичный рассмотренному выше, можно определить параметры парной регрессии, описываемой другими видами уравнений – гиперболой, параболой и др.