Алгоритм метода Гомори

Шаг 1. Симплекс-методом находим оптимальное решение задачи (22) без учета условия целочисленности. Если задача не имеет решения, то неразрешима и исходная задача ЦЛП. В этом случае алгоритм завершает работу.

Шаг 2. Пусть оптимальная таблица имеет вид:

	b		…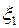
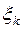
L			…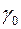
			…
…	…	…………..
			…

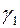
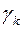
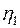
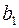
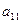
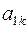
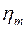
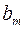
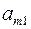
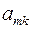
Если элементы 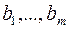– целочисленные, то оптимальное решение 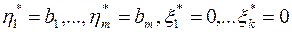является целочисленным. В этом случае вычисления заканчиваем. Иначе, переходим к следующему шагу.

Шаг 3. Среди дробных компонент 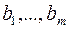таблицы выбираем элемент 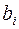с максимальной дробной частью 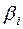и по строке i составляем дополнительное ограничение:

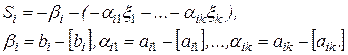
Здесь 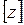– целая часть числа 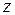(наибольшее целое число, не превышающее число ).

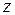Шаг 4. Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.

Замечания

Признаком отсутствия целочисленного решения служит появление в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами (поскольку соответствующее уравнение неразрешимо в целых числах).

На шаге 4 двойственный симплекс-метод применяется до тех пор, пока не будет получена оптимальная симплексная таблица (возможно, потребуется несколько итераций).

Если на шаге 4 в базис вводится переменная дополнительного ограничения 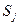, то эта строка вычеркивается из симплексной таблицы (соответствующее ограничение является избыточным).