Двойственный симплекс-метод

Метод работает с теми же симплексными таблицами, что и прямой симплекс-метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис [1,3].

Вычислительная схема двойственного симплекс-метода

Шаг 0. Начинаем с симплексной таблицы, где .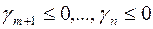

	B		…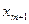
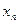
L			…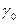
			…
…	…	…………..
			…

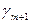
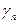
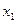
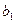
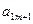
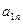
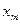
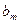
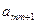
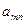
Шаг 1. Проверка на оптимальность. Если 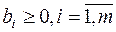, то решение 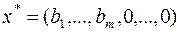– оптимальное.

Шаг 2. Выбор ведущей строки. Выбираем среди номеров i, для которых 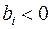, номер k с максимальным по модулю значением

.

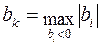Строка k объявляется ведущей.

Шаг 3. Проверка на неразрешимость. Если в строке 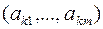нет отрицательных элементов, то двойственная целевая функция неограниченная и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.

Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки 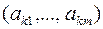элемент с номером s, для которого выполняется равенство

.

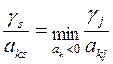Столбец s объявляется ведущим, а элемент 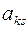– ведущим элементом.

Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).