Пример решения задачи методом искусственного базиса

Выделить допустимое базисное решение для задачи ЛП:

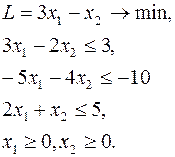
Приведем задачу к канонической форме на минимум с неотрицательными правыми частями:

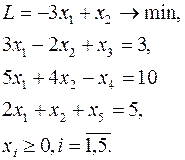
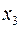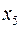Заметим, что переменные и можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.

Во вторую строку ограничений вводим искусственную переменную z, потому что в этой строке нет переменной, которую можно взять базисной, не проводя при этом дополнительных преобразований всей системы ограничений.

Полученная вспомогательная задача имеет вид

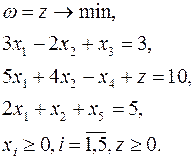
Приведем задачу к виду (16):

Выпишем соответствующую симплексную таблицу:

	B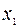
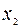
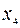
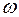
				-1
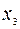
			-2
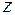
				-1

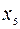
Ведущий столбец рекомендуется выбирать не по максимальному положительному элементу строки целевой функции, а так, чтобы из базиса выводилась искусственная базисная переменная (соответствующая ведущая строка должна быть строкой искусственной переменной). Так, выбрав ведущим столбцом столбец переменной 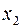, получим ведущую строку – строку с переменной z (выбирая ведущим столбцом 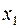, получили бы ведущую строку 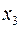, и из базиса выводилась бы переменная ).

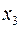Итак, искусственная переменная z выйдет из базиса, а переменная 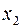введется в базис.

Симплексная таблица преобразуется к виду:

	B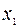
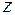
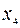
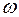
			-1
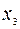
		11/2	1/2	-1/2
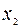
	5/2	5/4	1/4	-1/4
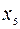
	5/2	3/4	-1/4	1/4

Так как значение 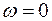, то полученный базис 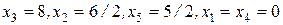является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию через небазисные переменные 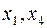, подставим значение базисной переменной 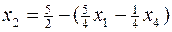в целевую функцию. В результате получим:

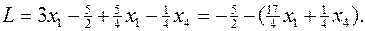
Тогда исходная задача будет иметь вид специальной формы задачи ЛП:

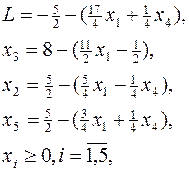
что и требовалось получить в результате решения вспомогательной задачи.