Алгоритм симплекс-метода для задачи на минимум

Шаг 0. Подготовительный этап.

Приводим задачу ЛП к специальной форме (15).

Шаг 1. Составляем симплекс-таблицу, соответствующую специальной форме:

	B		…		…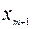
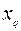
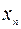
L			…		…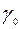
			…		…
..	..	…………
			…		…
..	..	…………
			…		…

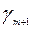
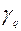
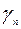
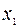
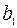
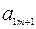
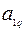
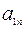
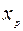
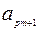
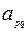
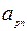
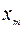
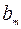
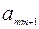
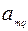
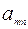
Заметим, что этой таблице соответствует допустимое базисное решение 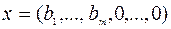задачи (15). Значение целевой функции на этом решении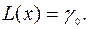

Шаг 2. Проверка на оптимальность

Если среди элементов индексной строки симплекс – таблицы 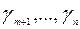нет ни одного положительного элемента то 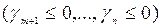, оптимальное решение задачи ЛП найдено: 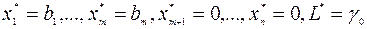. Алгоритм завершает работу.

Шаг 3. Проверка на неразрешимость

Если среди 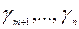есть положительный элемент 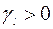, а в соответствующем столбце 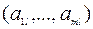нет ни одного положительного элемента 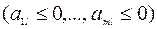, то целевая функция L является неограниченной снизу на допустимом множестве. В этом случае оптимального решения не существует. Алгоритм завершает работу.

Шаг 4. Выбор ведущего столбца q

Среди элементов 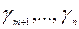выбираем максимальный положительный элемент 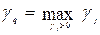.Этот столбец объявляем ведущим (разрешающим).

Шаг 5. Выбор ведущей строки p

Среди положительных элементов столбца 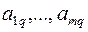находим элемент 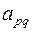, для которого выполняется равенство

.

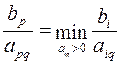Строку p объявляем ведущей (разрешающей). Элемент 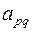объявляем ведущим (разрешающим).

Шаг 6. Преобразование симплексной таблицы

Составляем новую симплекс-таблицу, в которой:

а) вместо базисной переменной 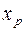записываем 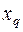, вместо небазисной пере менной 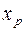записываем ;

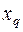б) ведущий элемент заменяем обратной величиной ;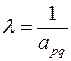

в) все элементы ведущего столбца (кроме 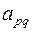) умножаем на ;

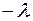г) все элементы ведущей строки (кроме 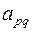) умножаем на ;

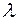д) оставшиеся элементы симплексной таблицы преобразуются по следующей схеме «прямоугольника».

Из элемента вычитается произведение трех сомножителей:

первый – соответствующий элемент ведущего столбца;

второй – соответствующий элемент ведущей строки;

третий – обратная величина ведущего элемента .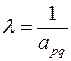

Преобразуемый элемент и соответствующие ему три сомножителя как раз и являются вершинами «прямоугольника».

Шаг 7. Переход к следующей итерации осуществляется возвратом к шагу 2.