Общие рекомендации к графическому решению задач ЛП
1. Графически могут решаться [1]:
a) задачи, заданные в произвольной форме, содержащие не более двух переменных;
b) задачи, заданные в канонической форме, с числом свободных переменных 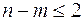 ;
;
c) задачи в произвольной форме записи, которые после приведения к канонической форме будут содержать не более двух свободных переменных 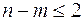 .
.
2. Основной формой для графического решения является 1-й тип задач. Поэтому, если встречается 2-й или 3-й тип задач, то предварительно их модель должна быть приведена к первому типу.
3. Решение задач 1-го типа выполняется в два этапа:
этап 1 – построение области допустимых решений;
этап 2 – построение в допустимой области оптимального решения.
4. При построении области допустимых решений может встретиться один из трех случаев:
а) пустая область – задача не имеет решения из-за несовместности системы ограничений в области допустимых решений;
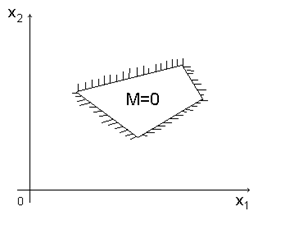
б) выпуклый многоугольник – задача всегда имеет оптимальное решение;
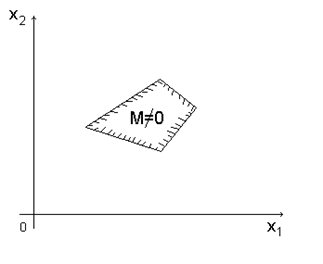
в) неограниченная выпуклая многогранная область – в зависимости от направления вектора c (вектора коэффициентов целевой функции L) задача может иметь или не иметь решение. Последнее связано с неограниченностью целевой функции в области допустимых решений.
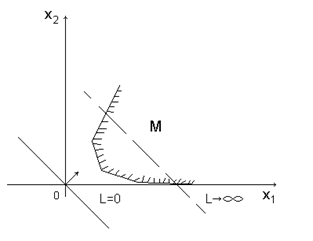
5. Если оптимальное решение существует, то возможен один из трех исходов:
а) оптимальное решение единственное и совпадает с одной из вершин области;
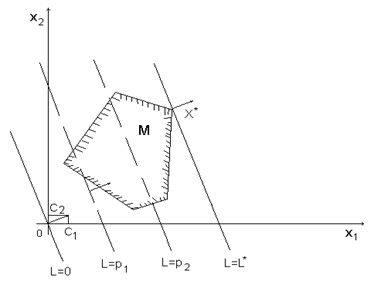
б) оптимальные решения соответствуют всем точкам отрезка, соединяющего две вершины области 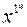 и
и 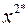 :
: 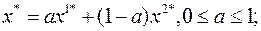
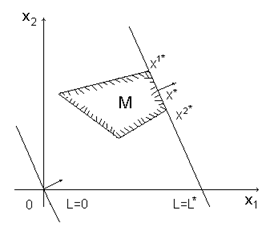
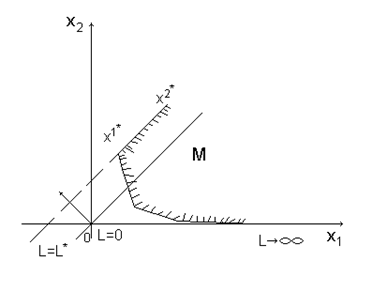
в) оптимальные решения соответствуют всем точкам допустимого луча, исходящего из вершины области 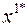 :
: 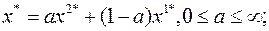
Дата добавления: 2017-09-19; просмотров: 574;
