Конструирование сказочных персонажей на основе фантограммы.

Конструирование сказочных персонажей на основе фантограм­мы происходит в форме выполнения упражнений, таких как, напри­мер, «Придумать фантастическое растение».

Как разъяснял Г.С. Альтшуллер, с математической точки зрения для подобных упражнений характерны: наличие некоторого исход­ного множества объектов (М) и необходимость дополнить это мно­жество одним или несколькими объектами, т.е. получить: М+ X.

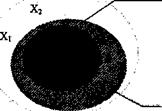
В качестве исходного множества могут выступать самые различ­ные группы объектов: животные, птицы, растения, цветы, разумные существа, машины, средства связи, планеты и т.д. Схематически ситуацию можно изобразить так (рис. 8).

Привычная зона

Пограничная зона

Рис.4. Схема конструирования на основе фантограммы

Решающий задачу человек находится где-то в центре множества М. Надо с помощью фантазии выйти за пределы М, найти новые, яркие и интересные объектыХ₁, Х₂, а не тривиальные, типа Z_1,Z₂ изпривычной зоны.

Основные трудностивыполнения упражнения следующие:

—отсутствует сколько-нибудь ясное представление о границах М;

—внимание отвлекается объектами из привычной зоны. Поэтому дети идут по пути наименьшего сопротивления: берут два объекта из привычной зоны и комбинируют их (этот прием известен им из сказок и мифов, где фигурируют русалка, кентавр и другие герои). Неясность границ М приводит к тому, что приду­манные объекты, даже если удается отойти от привычной зоны, не выходят за пределы пограничной зоны М(Y₁ ,Y₂).

Итак, сначала дети берут объекты в привычной зоне или возле нее и подвергают их простейшим изменениям (чаще всего — комбина­ционным), например, комбинируют кошку и птицу и получают «ле­тающую кошку». Однако, по мнению Альтшуллера, с точки зрения ТРИЗ, более интересны фантазии, основанные на изменении объектов из пограничной зоны (например, комбинация кошки и радиотелефона и т.п.), позволяющие выйти за пределы М. Для облегчения этого выхода он предлагал использовать фантограммы — таблицы, на од­ной оси которых перечислены типичные для разных множеств М показатели, а на другой — основные приемы их изменения (табл. 1).

Таблица 1