Современные технологии и направления в математическом развитии дошкольников.

У современных педагогов есть большие возможности для кон­струирования авторских программ по математическому развитию ребенка, что, однако, невозможно без глубокого знания основ те­ории и методики математики, обращения к успешно апробирован­ным традиционным, альтернативным и вариационным подходам к математической подготовке детей.

Актуальными для обогащения действующих и создания новых методик и технологий математического развития ребенка в све­те современных требований представляются направления, связанные с адаптированием к специфике детского возраста теории решения изобретательских задач (ТРИЗ), компьютерной среды, эвристичес­кого обучения, математического моделирования. Эти направления способствуют углублению дидактических ос­нов формирования математических представлений у детей с учетом преемственности между детским садом и начальной школой.

Интеллектуальная деятельность, основанная на активном поис­ке способов действий, уже в дошкольном возрасте может стать при­вычной и естественной, если усилия педагогов и родителей направ­лены на воспитание у ребенка потребности испытывать интерес к самому процессу познания, самостоятельному поиску решений и достижению поставленной цели.

По мнению многих исследователей, важными показателями ум­ственного развития ребенка к концу дошкольного возраста яв­ляются: сформированность образного и основ словесно-логичес­кого мышления, воображения, творчества, овладение умениями классифицировать, обобщать, схематизировать, моделировать, от­ражая и контролируя результаты познавательной деятельности в диалоге и монологе.

Следует помнить, что содержание деятельности по математи­ческому развитию ребенка при любом подходе должно соответствовать его возрастным особенностям и требованиям к подготовке, обеспечивающим дальнейшее развитие; учитывать возможности современных информационных технологий; предусматривать пути корректировки. Формы и методы работы определяются необходимостью реализации гуманистических идей игрового освоения мира, обеспечиваются личностно-ориентированным взаимодействием взрослых с детьми в процессе организации детской деятельности.

Представленные направления определяют педагогу сопровож­дающую позицию, т.е. предполагают возможность выбора детьми собственного пути решения образовательных задач и продвижения по нему в соответствии со своими особенностями, ведут к с хранению уникальности, разноуровневости и разноплановости дошкольников в рамках математики как сферы знания.

Анализ содержания действующих программ для дошкольных образовательных учреждений и начальной школы в области математического развития, и наблюдения экспериментальных исследований свидетельствуют о продуктивности синтеза теоретико-множественного подхода с изучение скалярных величин и их свойств. Эффективные подходы отличаются следующей логикой: «множество, величина — число отношение».

ТРИЗ-направление. Истоки развития и основные понятия теории решения изобретательских задач.

Существуют три основных подхода к решению лю­бой проблемы:

- метод проб и ошибок (МПиО);

- активизация перебора вариантов (МАПВ);

- сильные решения без сплошного перебора вари­антов (ТРИЗ).

Ученые Ф. Бэкон, Р. Декарт, А. Осборн, Ф. Цвики, Дж. Гордон и другие, синтезируя философский и ма­тематический подходы пытались усовершенствовать МПиО. Так возникли методы мозгового штурма (А. Ос­борн), синектики (Дж. Гордон), многомерных матриц (Ф. Цвики) и т.д. Слабые стороны МАПВ — отсутствие критериев решения, низкая управляемость и целенап­равленность процесса решения; движущее противоре­чие — выигрыш во времени при поиске разнообраз­ных вариантов решения и одновременно проигрыш при оценке полученных вариантов.

Теория решения изобретательских задач (ТРИЗ) закономерно появилась во второй половине XX в. как средство разрешения данного противоречия. Анализ де­сятков тысяч изобретательских патентов позволил ос­новоположнику ТРИЗ Г. С. Альтшуллеру сделать сле­дующий вывод: технические системы развиваются по объективно существующим законам, которые позна-ваемы, выявлены и предлагают сознательное совер­шенствование старых и создание новых систем. Откры­тая ученым и его последователями система законов развития технических систем легла в основу ТРИЗ.

Исторически сутью ТРИЗ является целенаправленный поиск решений, совмещенный с отбором из них силь­ных без сплошного перебора слабых. Базовые принципы, на основе которых ТРИЗ решает эту задачу, следующие:

—объективность законов: системы развиваются по объективным законам, которые надо изучать и использовать в процессе решения задач;

—наличие противоречия: проблема трудна, потому что содержит противоречие, которое следует выявить и разрешить;

—конкретность решения: конкретный ресурс приобретает кон­кретные свойства при конкретных обстоятельствах.

В результате своего развития ТРИЗ стала основой для создания практической методологии анализа проблем, возникающих при функционировании искусственных систем. В настоящее время на базе ТРИЗ формируется теория развития искусственных систем (ТРИС).

Отражая основные этапы мыслительных процессов анализа, данные теории все шире используются в системе образования, как базовая методология для развития культуры мышления и логики. Области современного применения ТРИЗ весьма широки: в построении сюжетов литературных произведений, живописи, ис­кусстве, биологии, математике и Методике математического развития , географии, педаго­гике и психологии.

Определим основные понятия ТРИЗ, используемые в математи­ческом развитии детей.

Алгоритм решения изобретательских задач (АРИЗ) — последова­тельность выполнения мыслительных операций, основанная на объективных законах развития технических систем и предназначен­ная для анализа технических проблем и поиска наиболее эффек­тивного их решения.

Алгоритм решения проблемных ситуаций (АРПС) — модифика­ция АРИЗ, основанная на объективных законах развития искус­ственных систем и предназначенная для анализа проблем и поис­ка наиболее эффективного их решения.

Система — совокупность элементов, образующих при объединении новое свойство, которым не обладают отдельно взятые элементы, предназначена для выполнения определенной функции.

Идеальная система — структура данной системы стремится к нулю, но способность выполнять свои функции при этом не уменьшается (иными словами, системы нет, а функция ее сохраняется и выпол­няется).

Надсистема — объединение, в которое сама система входит как составная часть.

Подсистема — часть системы.

Элемент системы — тривиальная часть системы (степень триви­альности условна, корректируется по смыслу понятием подсисте­мы).

Системный оператор — 3-, 9- или 18-экранная схема сильного мышления. Поясним: каждый предмет, объект или явление окружа­ющего мира можно рассмотреть как систему, которая входит в надсистему, являясь одной из ее частей; взаимодействуя с другими частями, сама система состоит из взаимодействующих частей — подсистем (см. рис.1).

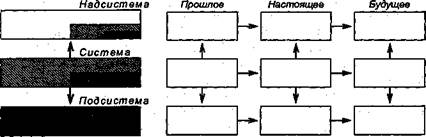
Рис. 1. Общая схема Рис. 2. Девятиэкранная схема

системного оператора системного оператора

Например, для понятия — десяток — система — одной из ближай­ших надсистем, в которую оно входит как составная часть, будет «сотня», а одной из подсистем — «единица». Для понятия «треугольник» надсистемным явится понятие «форма», подсистемным — «точка».

На каждом этапе 3-экранной схемы можно выделить линию раз­вития: прошлое, настоящее и будущее — получается 9-экранная схема (рис. 2).

Представим по 9-экранной схеме сильного мышления системное понятие «десяток» (рис. 3).

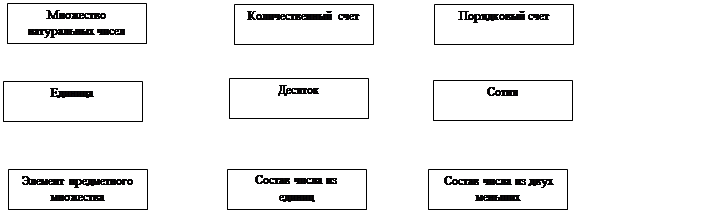
Рис. 3. Характеристика понятия «Десяток» с использованием системного оператора

На 9-экранной схеме в центре располагают базовое понятие (си­стему). Если определить для него антипод (антисистему) и соста­вить свою 9-экранную схему, в результате получим 18-экранную схему сильного мышления.

Изделие —. тот элемент, который надо изменить, переместить, изготовить, измерить и т.д. — то, ради чего создается система.

Инструмент — объект, непосредственно взаимодействующий с изделием с целью получения нужного результата.

Ресурсы — все, что может быть использовано для решения задачи: вещества; поля; информация; атрибуты, их значения и связанные с ними результаты (явления и эффекты).

Результат — итог применения ТРИЗ для разрешения конкрет­ной проблемы, выраженный в общедоступной форме: положитель­ный результат — желательный для постановщика задачи, отрица­тельный—нежелательный.

Идеальный конечный результат (ИКР) — получение всех поло­жительныхрезультатов без каких-либо отрицательных. Различают разные уровни идеальности, при которых отрицательный результат:

—исчезает при минимальных затратах;

—устраняется сам;

—исчезает, устраняя еще один или несколько отрицательных

результатов;

—превращается в положительный и т.д.

Противоречие — несоответствие двух признаков одному и тому же предмету. Типовая формулировка элементарного противоречия такова: для множества значений атрибута-функции атрибут-аргу­мент имеет значение А, но для другого множества значений атри­бута-аргумента атрибут-функция имеет значение не А. Другими словами, это свойство связи между двумя параметрами системы, при котором изменение одного из них в нужном направлении вызывает недопустимое изменение другого.

Фантограмма — таблица, содержащая перечисление типичных для разных множеств универсальных и конкретных показателей и ос­новных приемов их изменения. Применяется для развития вообра­жения на основе нетривиальной логики.