Применение статистических испытаний при нормировании и обосновании управленческих решений

Сложные производственные ситуации, особенно для больших систем, как правило, трудно описать аналитически. Поэтому и последствия принимаемых решений остаются труднопредсказуемыми. Проведение натурных экспериментов требует больших затрат времени, материальных средств, небезопасно для самого изделия и тем более действующего производства, которое в рыночных условиях взаимодействует с клиентурой – потребителями продукции или услуг. Кроме того, для реального производства трудно обеспечить сопоставимость при проведении натурного эксперимента, так как абсолютно сопоставимые аналоги (другие АТП, СТО и т.д.) отсутствуют. Последовательное сравнение нескольких решений на одном производстве также затруднено из-за неминуемого изменения во времени других факторов, влияющих на показатели эффективности, например спрос на услуги, цены, условия эксплуатации.

В этих условиях при принятии решений можно применять методы исследования и оценки систем на моделях.

Модель – это упрощенная форма представления реальных процессов и взаимосвязей в системе, позволяющая изучить, оценить и прогнозировать влияние составляющих элементов (факторов, подсистем) на поведение системы в целом, т.е. на изменение целевых показателей. Модели могут быть физическими, математическими, логическими, имитационными и др.

При решении технических, технологических и организационных задач, когда действует много факторов, в том числе и случайных, а информация неполная, получил распространение метод имитационного моделирования.

Имитационное моделирование – это процесс конструирования модели реальной системы и постановка экспериментов на этой модели с целью выяснения поведения системы, а также оценки различных стратегий, обеспечивающих ее функционирование без физических экспериментов на реальном объекте.

Процесс имитационного моделирования включает следующие основные этапы.

1 Описание системы, т.е. установление внутренних взаимосвязей, границ, ограничений и показателей эффективности системы, подлежащей изучению.

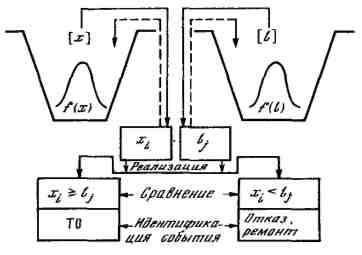
Рисунок 4.17 – Схема процесса имитационного моделирования

2 Конструирование модели — переход от реальной системы к определенной логической схеме, отображающей процессы, происходящие в системе.

3 Подготовка и отбор данных, необходимых для построения модели.

4 Трансляция модели, включающая описание модели на языке ЭВМ.

5 Оценка адекватности, позволяющая судить о корректности выводов, полученных на модели, для реальной системы.

6 Планирование экспериментов: объемов, последовательности.

7 Экспериментирование, заключающееся в имитации процессов реальной системы на модели и получении необходимых данных.

8 Интерпретация — получение выводов по результатам моделирования.

9 Реализация — практическое использование модели и результатов моделирования при принятии решения для реальной системы.

Рассмотрим процесс имитационного моделирования (рисунок 4.17) при определении периодичности ТО по безотказности (см. § 4.2) при условии, что случайной является не только наработка на отказ х_i но и фактическая периодичность ТО l_j которая также имеет некоторую вариацию относительно плановой.

В данном случае моделируется процесс предупреждения отказа элемента автомобиля при условии, что он подвергается профилактическим воздействиям с нормативной периодичностью 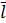₁ которая фактически имеет некоторую вариацию, характеризуемую законом распределения f(l), l, σ₁.

Модель процесса в данном примере – это формула риска, т.е. вероятность, что в условиях вариации наработки на отказ х_i и фактической периодичности ТО l_j риск отказа будет не больше допустимого (заданного): P(x_i<l_j)≤F_д.

Конструирование модели в примере – это создание двух массивов исходных данных [x] и [l]. Массивы данных могут формироваться на основе информации по соответствующим законам распределения случайных величин или включать фактические данные наблюдений, т.е. наборы х₁,х₂,..., х_i, и l₁, l₂,...,l_j.

Реализация – это извлечение из массивов данных в случайном порядке и сравнение двух случайных величин: х_i, и l_j.

Идентификация события происходит при каждой реализации и сравнении пары случайных величин: при х_i<l_j фиксируется отказ, а при х_i≥l_j —предупреждение отказа путем выполнения профилактической операции.

При многократном повторении определяется число отказов п₀и профилактики п_п, и оцениваются с определенной точностью вероятности соответствующих событий: отказа (риска) F=п₀/(п₀+п_п) и безотказной работы при выбранной периодичности l₁ R=п_п/(п₀+п_п).

Если фактический риск F_ф оказался больше допустимого F_д, то необходимо выбрать новую периодичность l₂<l₁ и повторить процесс имитационного моделирования до выполнения условий F_ф≤F_д.

На рисунке 4.18 приведена последовательность определения периодичности ТО по безотказности l^б и экономико-вероятностным методом l^э, при котором дополнительно учитываются еще две случайные величины — разовые затраты на выполнение ТО d_m и ремонт с_к (см. формулу (4.7) и рисунок 4.8). При моделировании представляется возможным оценить также предлагаемую наработку на отказ х_т, который может возникнуть с вероятностью F=1-R_Д равной произведению числа реализаций и принятой периодичности ТО l^б_о или l^э_о, деленному на зафиксированное число отказов п_о.

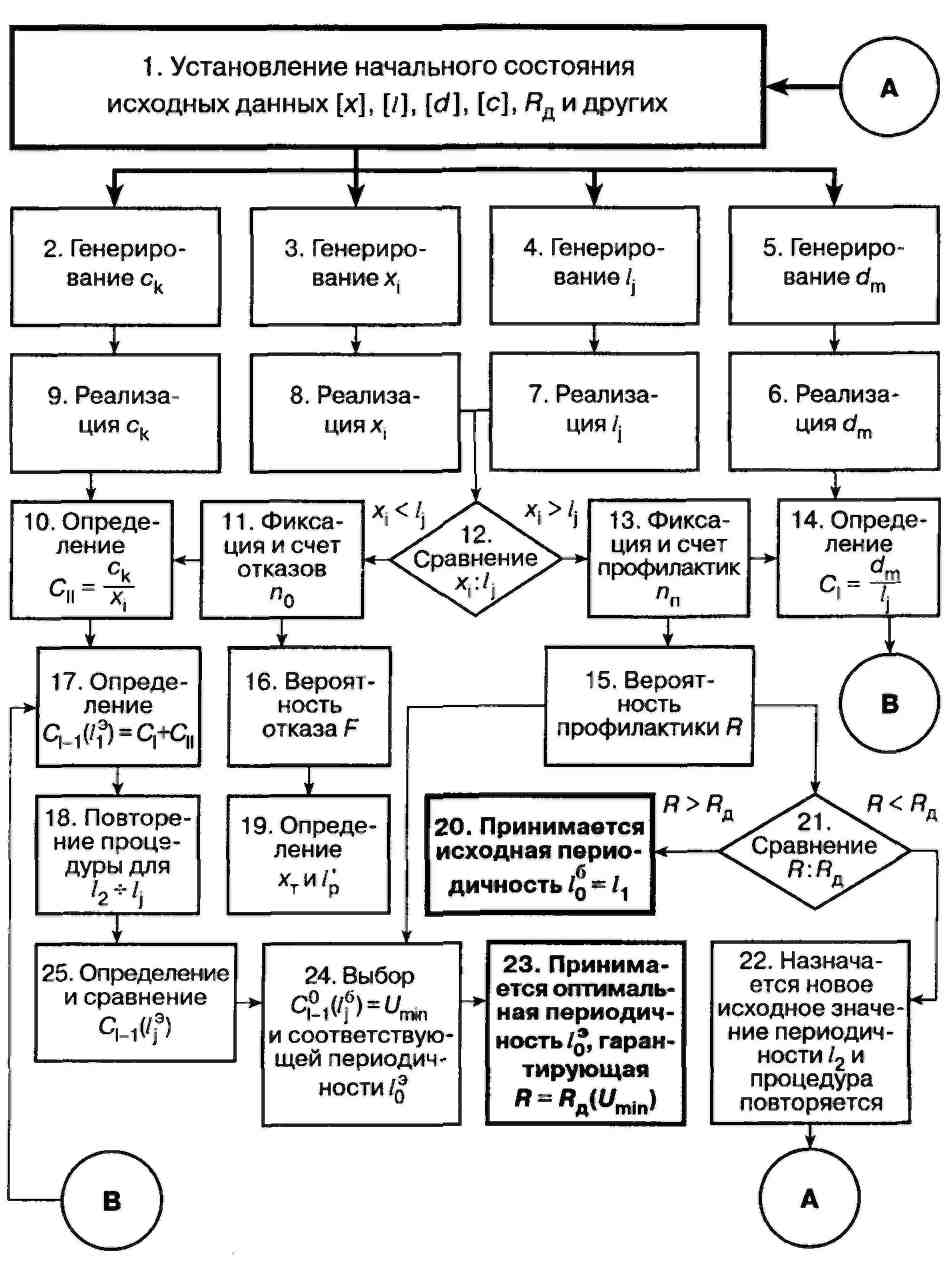
По безотказности: 1, 3, 4, 7, 8, 12, 11, 13, 15, 16, 19, 21, 20;

экономико-вероятностным методом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 11, 13, 15, 16, 19, 10, 14, 17, 18, 25, 24, 23

Рисунок 4.18 – Последовательность определения периодичности ТО методом имитационного моделирования

Моделирование влияния периодичности ТО на состояние тормозной системы автобуса большого класса может проводиться вручную или с использованием ПЭВМ.

На рисунке 4.19 показаны результаты имитационного моделирования, оценивающие влияние периодичности ТО на надежность тормозной системы городского автобуса. С увеличением периодичности ТО сокращается вероятность К выполнения контрольно-диагностической части операции (1), а вероятность отказа в межконтрольные периоды возрастает (4). Вероятность выполнения исполнительской части операции (5) сначала растет с увеличением периодичности ТО до оптимального значения в рассматриваемых условиях (3,5—4 тыс. км), а затем начинает сокращаться. Аналогичным образом изменяется и коэффициент повторяемости исполнительской части операции (2). Таким образом, при оптимальной периодичности ТО соотношение между контрольной и исполнительской частями операции будет также оптимальным.

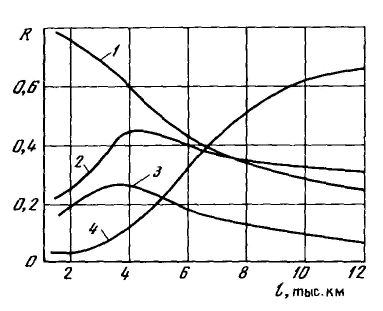
Рисунок 4.19 – Влияние периодичности ТО на состояние тормозной системы автобуса большого класса

По аналогичной схеме могут изучаться и оцениваться организационно-технологические ситуации, например работа системы массового обслуживания. В простейшем случае сравниваются интервалы и моменты поступления требований и продолжительность их выполнения. При усложнении модели может рассматриваться целесообразность реализации определенной дисциплины очереди: пропускать в первую очередь требования на ремонт автомобилей, дающих наибольший доход, или требования с малой продолжительностью обслуживания. В многоканальных системах возможно перераспределение требований или исполнителей по постам, оказание взаимопомощи и т.д. С помощью комбинации ряда подобных моделей конструируют имитационные модели зоны, участка, цеха и предприятия.

Имитационные модели используются при проведении деловых игр. Деловые (хозяйственные) игры – это метод имитации принятия управленческих решений в различных производственных ситуациях. При этом создается та или иная управленческая или производственная ситуация, для которой необходимо найти рациональный выход, т.е. принять решение. Критерием является степень приближения решения к оптимальному (которое известно организаторам деловых игр) и время, затраченное на принятие решения. Деловые игры проводятся по определенным правилам, регламентирующим поведение участников, их взаимодействие, критерии эффективности. Деловые игры используются при обучении и оценке персонала и исследовании сложных производственных систем.

При обучении персонала они используются для иллюстрации, разъяснения определенных закономерностей и понятий и закрепления знаний; для программного и целевого обучения определенных специалистов, например диагноста, оператора ЦУГТ и др.; для тренировки специалистов непосредственно на производстве. При обучении персонала деловые игры, как правило, разворачиваются в реальном масштабе времени. При исследовании производственных ситуаций применяется сжатый масштаб времени.

Деловые игры позволяют осуществлять предварительный отбор кадров, так как при этом можно оценить способности, профессиональные навыки и знания кандидатов на определенные рабочие места и должности специалистов, управленцев и операторов.