Классификация случайных процессов при технической эксплуатации автомобилей
Для описания сложных технических систем, в частности СМО, наиболее распространенным является аппарат марковских случайных процессов (названный в честь знаменитого русского математика А.А. Маркова). Их особенность заключается в том, что вероятность любого состояния системы (например, автомобиля, группы автомобилей) в будущем зависит только от ее состояния в настоящее время и не зависит от того, когда и какими путями система пришла в это состояние. Действительно, работоспособность автомобиля в будущем зависит только от его фактического технического состояния, к которому автомобиль может прийти по-разному.
Марковские процессы с дискретным состоянием и непрерывным временем (непрерывные цепи Маркова) характеризуют функционирование систем, у которых переход из одного состояния в другое происходит в случайные моменты времени, а сами состояния дискретны, например изделие работоспособно или отказало.
Если возможные состояния системы S1, S2,...,Sn определены, то это марковский случайный процесс с дискретным состоянием, который выражается в том, что система скачком переходит из одного состояния в другое. Sk→Sk+1. Если переходы осуществляются в заранее зафиксированные моменты времени (например, при ТО) t1, t2,...,tk, то это марковский случайный процесс с дискретным временем, а последовательность случайных переходов называется марковской цепью. Марковские процессы хорошо иллюстрируются графом состояния системы, на котором прямоугольниками отмечены сами состояния, а стрелками – направления переходов. Если на графе у стрелок указаны вероятности или плотности вероятности перехода, то он называется размеченным графом состояний (рисунок 5.1).
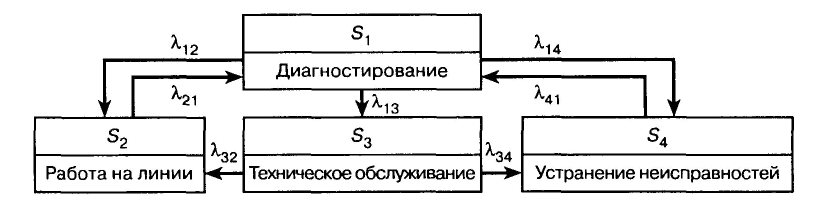
Рисунок 5.1 – Размеченный граф состояний для марковского процесса
с непрерывным временем
Для марковского процесса с дискретным состоянием и непрерывным временем рассматриваются плотности вероятностей λ переходов системы за время Δt; из состояния Si, в состояние Sj:
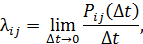
| (5.1) |
где Рij – вероятность того, что за Δt истема перейдет из состояния Si, в состояние Sj.
При малом Δt Рij(Δt)=λijΔt. Если все λij не зависят от t, то процесс называется однородным, а в противоположном случае – неоднородным.
Имея данные по плотностям вероятностей переходов λij можно рассчитать вероятности всех состояний системы в разные моменты времени, т.е. определить вероятность первого состояния Р1(і), второго Р2(і), и т.д.
Эти вероятности определяются из системы дифференциальных уравнений А.Н. Колмогорова, составляемых по следующим правилам:
1) в левой части уравнения помещается производная вероятности соответствующего состояния, например dP1/dt;
2) правая часть содержит столько членов, сколько переходов (стрелок в размеченном графе) связано с данным состоянием;
3) каждый член правой части уравнения равен произведению плотности вероятности перехода на вероятность того состояния, из которого переход осуществляется;
4) знак «+» ставится перед членами правой части уравнения при переходе в данное состояние, а знак «-» – при выходе из данного состояния.
Например, для размеченного графа состояний, изображенного на рисунок 5.1, записывается система уравнений:
| dP1/dt=-(λ12+λ13+λ14)P1+λ21P2+λ41P4; dP2/dt=λ12P1+λ32P3-λ21P2; dP3/dt=λ13P1-(λ32+λ34)P3; dP4/dt=λ14P1+λ34P3-λ41P4. | (5.2) |
В уравнении для краткости опущены индексы t, т.е. вместо Р(t)записано Р и т.д.
Так называемые предельные состояния (при t→∞), когда Рi=соnst, определяются из приведенной системы уравнений, у которых левые части приравниваются нулю, и условия, что Р1+Р2+Р3+Р4=1. Эти финальные вероятности характеризуют среднее время пребывания системы в соответствующих состояниях S1, S2, S3и S4, а в общем виде: S1, S2,...,Sn.
Одним из распространенных случаев марковского процесса с дискретным состоянием и непрерывным временем являются простейшие процессы, или потоки, обладающие свойствами стационарности, ординарности и отсутствия последствия.
Стационарным является поток, при котором вероятность возникновения событий (например, отказов) в течение определенного промежутка времени (или пробега) зависит только от длины этого промежутка и не зависит от начала отсчета времени. Для стационарного потока за наработку X количество событий (отказов, требований)
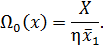
| (5.3) |
Ординарность означает, что вероятность возникновения на элементарном отрезке времени двух или более событий пренебрежима по сравнению с длиной самого участка. Применительно к описанию надежности ординарность означает, что одновременное возникновение двух разных отказов у автомобиля практически мало вероятно.
Отсутствие последствия – это независимость характера потока от числа ранее поступивших отказов и моментов их возникновения. На практике суммирование не менее шести—восьми элементарных потоков приводит к образованию простейшего или близкого к нему потока.
Для простейшего потока отказов вероятность возникновения определенного числа отказов в течение времени определяется законом Пуассона:
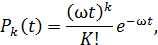
| (5.4) |
где k=0, 1, 2… отказов число отказов, возникающих за время t;
ω — параметр потока
В реальных условиях производства значение t обычно принимают равным 1, например 1 ч, 1 смена, 1 неделя, т.е. t=1, а ω t=Ω0=а —среднее число отказов, возникающих за время t. В этом случае
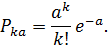
| (5.5) |
Используя последнюю формулу, можно установить вероятность появления определенного числа требований Рk при известном значении а.
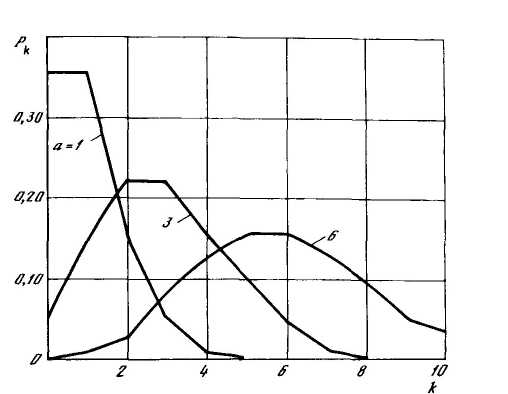
Рисунок 5.2 – Вероятность возникновения требований по закону Пуассона
в зависимости от их среднего числа а
Например, при а=3 вероятность отсутствия требований
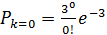 =0,05, или 5 %;
=0,05, или 5 %;
вероятность появления одного требования – 0,15; двух – 0,22; трех – тоже 0,22; четырех – 0,16 и т.д. (рисунок 5.2). Таким образом, загрузка постов и оборудования носит вероятностный характер: в примере у 22 % всех смен будет фактическое число требований, совпадающее со средним, у 42 % (5+15+22) загрузка будет меньше, а в 36 % (100-22-42) случаев – больше средней.
Следовательно, расчет производственных помещений, оборудования, штата рабочих, т.е. пропускной способности предприятия (участка, поста), исходя из средней потребности может привести или к неполной загрузке зон и участков, или к необходимости ожидания момента обслуживания, т.е. к образованию очереди требований. Иными словами, необходима оптимизация систем обслуживания, под которой понимается соответствие функционирования этих систем определенным критериям эффективности. При этом возможны два подхода, которые условно можно назвать внутренними (для предприятия) и внешними (для клиентуры).
При первом подходе, свойственном функционированию ИТС в рамках системы более высокого уровня (например, комплексное АТП), сопоставляются за определенный промежуток времени затраты, связанные с простоем автомобиля в ожидании ремонта или обслуживания Са и простоем оборудования и ремонтного персонала в ожидании автомобилей Сор.
По мере роста показателей, влияющих на пропускную способность средств обслуживания Z (число постов, исполнителей, оснащение технологическим оборудованием и инструментом), затраты, связанные с простоем автомобилей в ожидании обслуживания, сокращаются (кривая 1 на рисунке 5.3), а затраты, вызванные простоем средств обслуживания и персонала в ожидании загрузки, возрастают (кривая 2 на рисунке 5.3).
Минимальное значение суммы этих затрат (кривая 3 на рисунке 5.3), являющейся целевой функцией, и будет соответствовать оптимальной структуре обслуживания (например, число постов, исполнителей), при которой минимизируются потери предприятия, связанные с простоем средств обслуживания, ожиданием объектов обслуживания.
При втором подходе, характерном для обслуживания внешней по отношению к предприятию клиентуры, целевая функция направлена на максимизацию прибыли ПZ, получаемой от функционирования системы обслуживания, при разных показателях Z. В этом случае наблюдается несколько зон функционирования системы обслуживания (рисунок 5.4).
Характерным признаком рассматриваемого закона Пуассона является равенство дисперсии среднему значению, поэтому коэффициент вариации потока требований υ=а-0,5. Это означает, что с увеличением программы вариация ее фактического значения сокращается. Например, при средней программе а=1; υ=1; а=3; υ=0,58; а=5, υ=0,45; а=25, υ=0,2, т.е. распределение становится более симметричным с увеличением программы (см. рисунок 5.2 при а=6), что благоприятно сказывается на организации технологического процесса ТО и ремонта.
Поэтому укрупнение предприятий, централизация и кооперирование ТО и ремонта, приводящие к увеличению программы работы, – это направления совершенствования технической эксплуатации автомобилей.
Еще одним важным свойством простейшего потока является то, что изменение промежутка времени между двумя соседними событиями (требованиями) подчиняется экспоненциальному закону распределения.
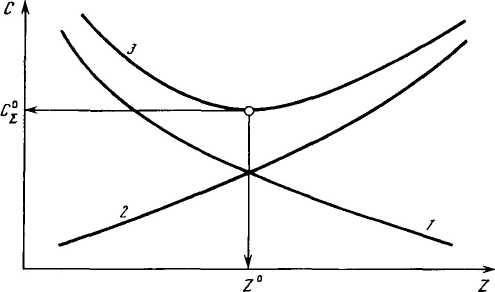
Затраты: 1 — от простоев автомобилей; 2 —системы обслуживания в ожидании требований на обслуживание; 3 — суммарные
Рисунок 5.3 – Определение показателей пропускной способности систем обслуживания технико-экономическим методом
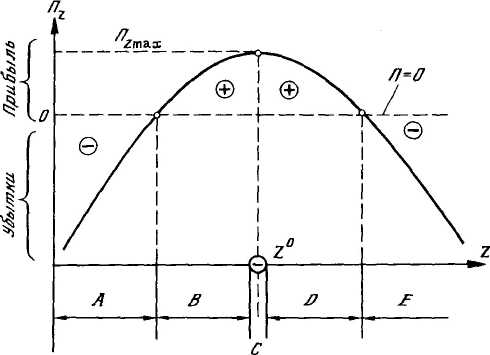
А, Е —зоны убытков предприятии: А —в результатс недостаточной пропускной способности средств обслуживания (очередь, потеря клиентуры); Е — в результате недогрузки и простоев средств обслуживания; В, D — зоны устойчивой, но разной, С — максимальной при оптимальных показатслях прибыли
Рисунок 5.4 – Зависимость прибыли от показателей Z системы обслуживания предприятия
Если поток обладает только двумя свойствами (ординарностью и отсутствием последствия), то он называется нестационарным пуассоновским, и тогда в течение смены число событий за интервал (t,t+τ) определяется следующим образом:
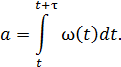
| (5.6) |
Стабилизация параметра потока отказов или ее приведение на отдельных участках к стабильному значению (см. рисунок 5.6) позволяет рассматривать потоки как простейшие, или пуассоновские, и применять для характеристики потока уравнение Пуассона.
Если в марковских процессах с непрерывным временем все дискретные состояния располагаются в последовательную цепь с переходами, показанными на рисунок 5.5, то это так называемый процесс гибели и размножения. Очевидно, для первого состояния имеется равновесие λ12P1=λ21P2, для второго состояния λ23P2+λ21P2=λ12P1+λ32P3, но, учитывая равенство для первого состояния, имеем λ23P2=λ32P3, т.е. для данного процесса имеет место соотношение λk-1,kPk-1=λk,k-1Pk, где k принимает значение от 2 до п.
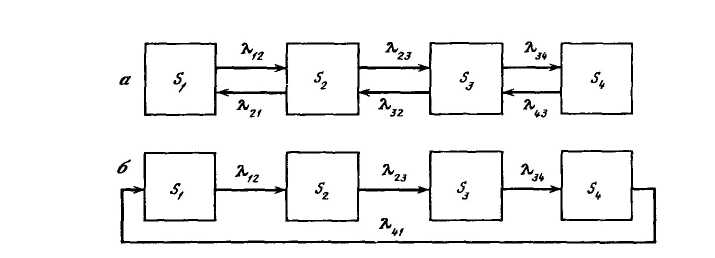
а – «гибели и размножения»; б – циклического
Рисунок5.5 – Схемы марковских процессов
Используя это соотношение, а также условие Р1+Р2+...+Рп=1, определяем предельные вероятности
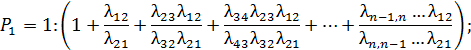
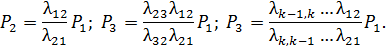
| (5.7) |
Например, на крупном АТП имеется компрессорная станция, состоящая из трех одинаковых компрессоров, средняя наработка на отказ каждого из которых составляет  . Поток отказов простейший. Среднее время ремонта равно
. Поток отказов простейший. Среднее время ремонта равно 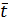 р. Определить среднюю производительность станции при условии, что производительность трех компрессоров W1=100 %: двух – W2=70 % и одного – W3=35 %.
р. Определить среднюю производительность станции при условии, что производительность трех компрессоров W1=100 %: двух – W2=70 % и одного – W3=35 %.
Поток отказов одного компрессора по условию является простейшим с экспоненциальным распределением наработки между отказами и параметром λ=1/  .
.
Если работают все три компрессора (состояние S1), то потоки отказов суммируются и возрастают в три раза, т.е. λ12=3/  (см. рисунок 5.5, а). При работе двух компрессоров (состояние S2) λ23=2/
(см. рисунок 5.5, а). При работе двух компрессоров (состояние S2) λ23=2/  , одного (состояние S3) – λ34=1/
, одного (состояние S3) – λ34=1/  . При состоянии S4 все три компрессора ремонтируются.
. При состоянии S4 все три компрессора ремонтируются.
В рассматриваемой модели необходимо учитывать не только интенсивность отказов, но и интенсивность восстановления μ, которая при экспоненциальном законе распределения продолжительности восстановления равна величине, обратной средней продолжительности ремонта 1/ 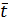 р, т.е. при работе одного компрессора μ1=λ12=1/
р, т.е. при работе одного компрессора μ1=λ12=1/ 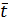 р, двух – μ2=λ32=2/
р, двух – μ2=λ32=2/ 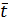 р, трех – μ3=λ43=3/
р, трех – μ3=λ43=3/ 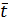 р. С учетом (5.7) и для
р. С учетом (5.7) и для  =50 ч и
=50 ч и 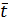 р=4 ч имеем
р=4 ч имеем
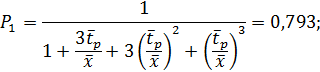
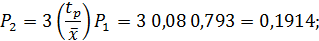
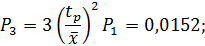
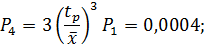
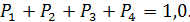
Средняя производительность компрессорной станции в установившемся режиме Если средняя наработка на отказ будет ниже, например 32 ч, то вероятности соответственно составят: Р1=0,702; Р2=0,265; Р3=0,032; Р4=0,001, а средняя производительность компрессорной станции сократится до 0,89W1, или на 4,5 %.
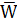 =P1W1+P2W2+P3W3+P4W4=0,79W1+0,19W1+0,015 0,35W1=0,93W1.
=P1W1+P2W2+P3W3+P4W4=0,79W1+0,19W1+0,015 0,35W1=0,93W1.
Если в марковском процессе с непрерывным временем дискретные состояния связаны между собой в одно кольцо и имеют односторонние переходы, то такой процесс называется циклическим. Например, автомобиль последовательно (рисунок 5.5, б) может быть исправным и работать (S1), ожидать ремонта (S2), ремонтироваться (S3), ожидать работы после ремонта (S4) и снова работать (S1). Плотность вероятности переходов будет соответственно λ12, λ23, λ34, λ41. Для предельных вероятностей, т.е. dP/dt=0, и при переходе из первого во второе состояние имеем λ12 P1=λ23 P2, далее λ23 P2=λ34 P3 …×
×λk-1,k Pk-1=λk,k-1 Pk. При переходе в последнее состояние λn-1,n Pn-1=λn,n-1 Pn, при переходе из последнего в первое λn,1 Pn=λ1,2 P1. Решая эту систему уравнений, получим
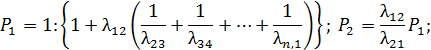
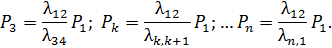
| (5.8) |
Т.к. рассматриваемый процесс – пуассоновский, среднее время пребывания системы в состоянии Si: 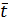 i=1/λi,i+1, откуда
i=1/λi,i+1, откуда
λi,i+1=1/ 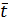 i; λn,1=1/ i; λn,1=1/ 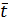 n. n.
| (5.9) |
С учетом (5.8) и (5.9)
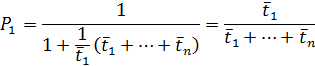
или в общем виде
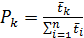 . .
| (5.10) |
Определим предельные вероятности для случая, рассмотренного на рисунке 5.5, б, при условии, что
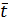 1=Tн;
1=Tн; 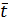 2=0,3Tн;
2=0,3Tн; 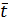 3=0,19Tн;
3=0,19Tн; 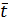 4=0,8Tн,
4=0,8Tн,
где Tн — среднее время нахождения автомобиля в наряде.
Р1=1/2,29=0,44; Р2=0,13; Р3=0,08; Р4=0,35. Сумма Р равна единице.
Преимуществом теоретических моделей (типа (5.3)—(5.10) и др.) в отличие от экспериментального подхода, который фиксирует простейшие события и показатели, соответствующие определенному моменту времени и состоянию системы, является возможность предвидеть поведение и состояние системы при изменении действующих на нее факторов.
Дата добавления: 2017-08-01; просмотров: 1339;
