Структура и показатели эффективности систем массового обслуживания
Система массового обслуживания состоит из следующих элементов (рисунок 5.6).
1 — входящий поток требований ω(t) – совокупность требований к СМО на проведение определенных работ (заправка, мойка, ТО и др.) или оказание услуг (покупка изделий, деталей, материалов и др.). Входящий поток требований может быть постоянным и переменным.
Требования бывают однородные (одинаковые виды работ или услуг) и неоднородные (разные виды работ или услуг).
2 — очередь – требования, ожидающие обслуживания. Очередь оценивается средней длиной r – числом объектов или клиентов, ожидающих обслуживания.
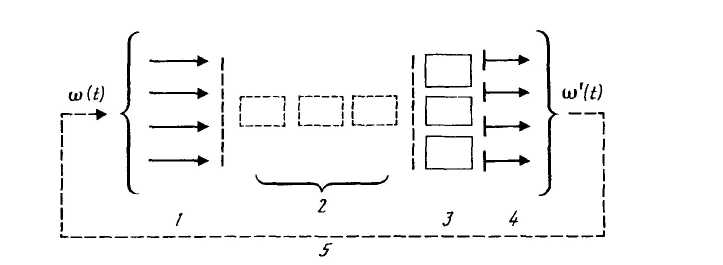
Рисунок 5.6 – Общая схема системы массового обслуживания
3 — обслуживающие аппараты (каналы обслуживания) – совокупность рабочих мест, исполнителей, оборудования, осуществляющих обслуживание требований по определенной технологии.
4 — выходящий поток требований ω’(t) – поток требований, прошедших СМО. В общем случае выходящий поток может состоять из требований обслуженных и необслуженных. Пример необслуженных требований: отсутствие нужной детали для автомобиля, находящегося в ремонте.
5— замыкание (возможное) СМО – состояние системы, при котором входящий поток требований зависит от выходящего.
На автомобильном транспорте после обслуживания требований (ТО, ремонт) автомобиль должен быть технически исправным.
Системы массового обслуживания классифицируются следующим образом.
1 По ограничениям на длину очереди:
— СМО с потерями – требование покидает СМО необслуженным, если в момент его поступления все каналы заняты;
— СМО без потерь – требование занимает очередь, даже если все каналы
заняты;
— СМО с ограничениями по длине очереди m или времени ожидания: если существует ограничение на очередь, то вновь поступившее (m+1)-е требование выбывает из системы необслуженным (например, ограниченная емкость накопительной площадки перед АЗС).
2 По количеству каналов обслуживания п:
— одноканальные: n=1;
— многоканальные n≥2.
3 По типу обслуживающих каналов:
— однотипные (универсальные);
— разнотипные (специализированные).
4 По порядку обслуживания:
— однофазовые – обслуживание производится на одном аппарате (посту);
— многофазовые – требования последовательно проходит несколько аппаратов обслуживания (например, поточные линии ТО; конвейерная сборка автомобиля; линия внешнего ухода: уборка → мойка → обсушка → полировка).
5 По приоритетности обслуживания:
— без приоритета – требования обслуживаются в порядке их поступления на СМО;
— с приоритетом – требования обслуживаются в зависимости от присвоенного им при поступлении ранга приоритетности (например, заправка автомобилей скорой помощи на АЗС; первоочередной ремонт на АТП автомобилей, приносящих наибольшую прибыль на перевозках).
6 По величине входящего потока требований:
— с неограниченным входящим потоком;
— с ограниченным входящим потоком (например, в случае предварительной записи на определенные виды работ и услуг).
7 По структуре СМО:
— замкнутые – входящий поток требований при прочих равных условиях зависит от числа ранее обслуженных требований (комплексное АТП, обслуживающее только свои автомобили (5 на рисунке 5.6));
— открытые – входящий поток требований не зависит от числа ранее обслуженных: АЗС общего пользования, магазин по продаже запасных частей.
8 По взаимосвязи обслуживающих аппаратов:
— с взаимопомощью – пропускная способность аппаратов непостоянна и зависит от занятости других аппаратов: бригадное обслуживание нескольких постов СТО; использование «скользящих» рабочих;
— без взаимопомощи – пропускная способность аппарата не зависит от работы других аппаратов СМО.
Применительно к технической эксплуатации автомобилей находят распространение замкнутые и открытые, одно- и многоканальные СМО, с однотипными или специализированными обслуживающими аппаратами, с одно- или многофазовым обслуживанием, без потерь или с ограничением на длину очереди или на время нахождения в ней.
В качестве показателей эффективности работы СМО используют приведенные ниже параметры.
Интенссивность обслуживания
| μ=1/tд, | (5.11) |
где tд — продолжительность (длительность) обслуживания одного требования.
Приведенная плотность потока требований
| ρ=ω/μ, | (5.12) |
где ω — параметр потока требований.
Абсолютная пропускная способность показывает количество требований, поступающих в единицу времени, т.е.
| A=ωg, | (5.13) |
где g— относительная пропускная способность.
Относителъная пропускная способность определяет долю обслуженных требований от общего их количества.
Вероятность того, что все посты свободны Р0, характеризует такое состояние системы, при котором все объекты исправны и не требуют проведения технических воздействий, т.е. требования отсутствуют.
Вероятность отказа в обслуживании Ротк имеет смысл для СМО с потерями и с ограничением по длине очереди или времени нахождения в ней. Она показывает долю «потерянных» для системы требований.
Вероятность образования очереди Рочопределяет такое состояние системы, при котором все обслуживающие аппараты заняты, и следующее требование «встает» в очередь с числом ожидающих требований r.
Зависимости для определения названных параметров функционирования СМО определяются ее структурой.
| tож=r/ω. | (5.14) |
Количество требований, связанных с системой,
| k=r+nзан, | (5.15) |
где nзан — среднее количество занятых постов.
Время связи требования с системой:
— СМО с потерями
| tсист=gtд; | (5.16) |
— СМО без потерь
| tсист=tд+tож. | (5.17) |
Издержки от функционирования системы
| И=С1r+С2nсн+(С1+C2)ρ, | (5.18) |
где С1 — стоимость простоя автомобиля в очереди;
r — средняя длина очереди;
С2 —стоимость простоя обслуживающего канала;
nсн — количество простаивающих (свободных) каналов;
tож — среднее время нахождения в очереди.
Из-за случайности входящего потока требований и продолжительности их выполнения всегда имеется какое-то среднее число простаивающих автомобилей. Поэтому требуется так распределить число обслуживающих аппаратов (постов, рабочих мест, исполнителей) по различным подсистемам, чтобы И=min. Этот класс задач имеет дело с дискретным изменением параметров, так как число аппаратов может изменяться только дискретным образом. Поэтому при анализе системы обеспечения работоспособности автомобилей используются методы исследования операций, теории массового обслуживания, линейного, нелинейного и динамического программирования и имитационного моделирования.
Пример. Станция технического обслуживания имеет один пост диагностирования (п=1). Длина очереди ограничена двумя автомобилями (т=2). Определить параметры эффективности работы диагностического поста, если интенсивность потока требований на диагностирование в среднем А=2 треб./ч, продолжительность диагностирования tд=0,4 ч.
Интенсивность диагностирования μ=1/0,4=2,5.
Приведенная плотность потока ρ=2/2,5=0,8.
Вероятность того, что пост свободен,
P0=(1-ρ)/(1-ρm+2)=(1-0,8)/(1-0,84)=0,339.
Вероятность образования очереди
Pоч=ρ2Р0=0,82 0,339=0,217.
Вероятность отказа в обслуживании
Pотк=ρm+1(1-ρ)/(1-ρm+2)=0,83(1-0,8)/(1-0,84)=0,173.
Относительная пропускная способность
g=1-Pотк=1-0,173=0,827.
Абсолютная пропускная способность
А=2 0,827=1,654 треб./ч.
Среднее количество занятых постов или вероятность загрузки поста
nзан=(ρ-ρm+2)/(1-ρm+2)=(0,8-0,84)/(1-0,84)=0,661=1-P0.
Среднее количество требовниий, находящихся вочереди,
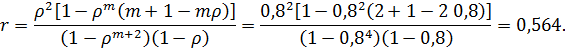
Среднее время нахождения требования в очереди
tож=r/ω=0,564/2=0,282 ч.
Пример. На автотранспортном предприятии имеется один пост диагностирования (п=1). В данном случае длина очереди практически неограниченна. Определить параметры эффективности работы диагностического поста, если стоимость простоя автомобилей в очереди составляет С1=20 ре (расчетных единиц) в смену, а стоимость простоя постов С2=15 ре Остальные исходные данные те же, что и для предыдущего примера.
Интенсивность диагностирования и приведенная плотность потока остаются теми же: μ=2,5, ρ=0,8.
Вероятность того, что пост свободен
P0=1-ρ=1-0,8=0,2.
Вероятность образования очереди
Pоч=ρ2Р0=0,82 0,2=0,128.
Относительная пропускная способность g=1, так как все намеченные автомобили пройдут через диагностический пост.
Абсолютная пропускная способность А=ω=2 треб./ч.
Среднее количество занятых постов nзан=ρ=0,8.
Среднее количество требований, находящихся в очереди,
r=ρ2/(1-ρ)=0,82/(1-0,8)=3,2.
Среднее время ожидания в очереди
tож=ρ2/(1-ρ)/μ=0,82/(1-0,8)/2,5=1,6.
Издержки от функционирования системы
И=С1r+С2nсн+(С1+C2)ρ=20 3,2+15 0,2+(20+15) 0,8=95,0 ре/смену.
Пример. На том же автотранспортном предприятии число постов диагностирования увеличено до двух (n=2), т.е. создана многоканальная система. Так как для создания второго поста необходимы капиталовложения (площади, оборудование и т.д.), то цена простоя средств обслуживания увеличивается до С’1=22 ре. Определить параметры эффективности работы системы диагностирования. Остальные исходные данные те же, что для предыдущего примера.
Интенсивность диагностирования и приведенная плотность потока остаются теми же: μ=2,5, ρ=0,8.
Вероятность того, что оба поста свободны,
Р0=1: 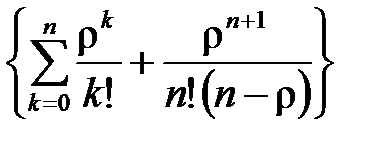 =0,294.
=0,294.
Вероятность образования очереди
Pоч=ρnР0 /n!=0,82 0,294/2=0,094,
т.е. на 37 % ниже, чем в предыдущем примере.
Относительная пропускная способность g=1, так как все автомобили пройдут через диагностические посты.
Абсолютная пропускная способность А=2 треб./ч.
Среднее количество занятых постов nзан=ρ=0,8.
Среднее количество требований, находящихся в очереди,
r=ρPоч/(n-ρ)=0,82 0,094/(2-0,8)=0,063.
Среднее время нахождения в очереди
tож=Pоч/(n-ρ)/μ=0,094/(2-0,8)/2,5=0,031.
Издержки от функционирования системы
И=С1r+С2nсн+(С1+C2)ρ=20 0,063+22 1,2+(20+22) 0,8=61,26 ре/смену,
т.е. в 1,55 раза ниже, чем при тех же условиях для одного диагностического поста, главным образом за счет сокращения очереди автомобилей на диагностику и времени ожидания автомобилей более чем в 50 раз. Следовательно, строительство второго диагностического поста в рассматриваемых условиях целесообразно. Используя формулу (5.18) из условия И1=И2, можно оценить предельные значения цены простоя средств обслуживания при строительстве и оснащении второго диагностического поста, которая в рассмотренном примере составляет C2пр=39 ре.
Дата добавления: 2017-08-01; просмотров: 1363;
