Количественные методы оценки рисков
Оценить риски можно с помощью двух методов: математического и теории зон риска [36, 67, 69, 79, 81].
Математическая оценка рисков
При оценке риска вполне обосновано применение аппарата математической статистики и теории вероятностей в случаях:
· инновации, имеющие аналоги – применяются методы математической статистики для оценки наиболее вероятных параметров инновационного процесса и его результатов;
· инновации, не имеющие аналогов, или организация-инноватор не обладает достаточным опытом для внедрения инновации, или инновационный процесс реализуется в условиях нестабильности – теория вероятностей, позволяющая моделировать инновационные процессы с большей точностью, определять меры по управлению риском;
· стохастические методы – моделирование результатов инновационной деятельности с учетом разработанных мероприятий по снижению рисков и оценки их эффективности.
Для представления риска в инновационной деятельности необходима:
· объективные закономерности, определяющие результат и ход инновационной деятельности;
· подтверждение этих закономерностей статистическими наблюдениями за инновационной деятельностью (ход реализации конкретной инновации и ее результат непредсказуем);
· статистика инновационных процессов подчиняется общим правилам математической статистики;
· важнейшие характеристики риска – вероятность возникновения неблагоприятной ситуации в ходе инновационной деятельности и количественная оценка этой «неблагоприятности»;
· количественная оценка риска инновационной деятельности – с учетом экономических и других аспектов инновационной деятельности, а также с применением комплексной оценки по нескольким аспектам процессов реализации нововведений.
Описание риска инновационной деятельности можно провести с применением следующей формулы:
R = F(p,u), (12.2)
где F – функция описания риска; р – вероятность неблагоприятной ситуации в ходе реализации нововведений; u – количественная оценка «неблагоприятности» ситуации в ходе реализации нововведений.
Для рисковых инноваций в первую очередь оценивается параметр наиболее ожидаемого результата (re), определяемый по формуле математического ожидания:
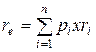 , (12.3)
, (12.3)
где r – первый возможный результат инновации; pj – вероятность i-го результата;n – число возможных результатов.
Пример 3. Инновационная компания разработала новый витамин, стимулирующий творческую активность персонала. Затраты на проведение исследований и испытаний препарата составили 20 тыс. руб. К препарату проявили интерес две фармацевтические компании. Они готовы купить сырье для производства витамина за 40 тыс. руб. Себестоимость сырья для фирмы-инноватора составит 10 тыс. руб. Вероятность того, что компании купят или не купят сырье, одинакова: 50:50. Возможные результаты инновационной деятельности представлены следующими вариантами (табл. 12.1):
· ни одна из компаний не купит сырье: фирма-инноватор понесет убытки в размере затрат на проведение исследований и испытаний (20 тыс. руб.);
· сырье и технологию производства приобретет лишь одна из компаний, тогда прибыль фирмы-инноватора составит: 40 - 10 - 20 = 10 тыс. руб.;
· сырье и технологию закупят обе фармацевтические компании:
· (40 - 10) 2 - 20 = 40 тыс. руб.
Таблица 12.1. Возможные результаты инновационной деятельности (тыс. руб.)
| Возможный результат | 1-я компания | Вероятность | |||
| купит | не купит | ||||
| 2-я компания | купит | +40 | +10 | 0,5 | |
| не купит | + 10 | -20 | 0,5 | ||
| Вероятность | 0,5 | 0,5 |
Тогда наиболее ожидаемый доход от инновации составит:
rе = 40 · 0,5 · 0,5 + 10 · 0,5 ·0,5 + 10 ·0,5 ·0,5 - 20 ·0,5 ·0,5 = +10 тыс. руб.
Количественной оценкой риска той или иной инновации принято считать вариацию (var) – разброс возможных результатов инновационной операции относительно ожидаемого значения (математического ожидания), рассчитывается как среднее квадратичное отклонение от ожидаемого результата:
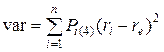 . (12.4)
. (12.4)
Также для оценки риска используется показатель среднего линейного отклонения (σ), который иногда называется дисперсией:
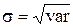 . (12.5)
. (12.5)
Относительное линейное отклонение оценивается с помощью показателя стандартного отклонения, или колеблемости (γ):
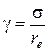 . (12.6)
. (12.6)
Чем выше коэффициент вариации, или колеблемость, тем более рискованной считается инвестиция. Для инновационной фирмы в приведенном примере №3 данные показатели составят:
var = (40 - 10)2 · 0,5 ·0,5 + (10 - 10)2 ·0,5 ·0,5 +(10 - 10)2 ·0,5 ·0,5 + (-20 - 10)2 ·0,5 · ·0,5 = 450.
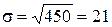 тыс. руб.
тыс. руб.
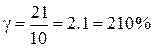 .
.
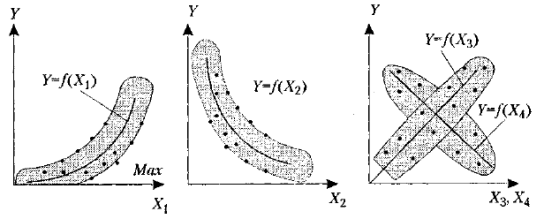
Наиболее упрощенный метод оценки рисков: на первом этапе рекомендуется попытаться установить зависимости между внешними (внутренними) факторами и уровнем риска. Количество зависимостей определяется полнотой и качеством информационного обеспечения системы управления рисками. Для этих целей следует строить корреляционные поля (рис. 12.1, б, в) и устанавливать статистические зависимости.
а) б) в)
Рис. 12.1. Корреляционные поля зависимостей уровня риска (У) от
факторов риска (X1, Х2, Х3, Х4)
На рис. 12.1 показаны криволинейная (Х1) и прямолинейная (Х3) прямо пропорциональные зависимости факторов от функции (риска) и соответствующие обратно пропорциональные зависимости (Х2 и Х4).
В первом случае (X1 и X3) с увеличением (ростом, повышением) фактора растет риск вложения инвестиций или выполнения какого-либо проекта. Например, с повышением степени износа основных производственных фондов (постоянного капитала) организации, среднего возраста технологии, текучести кадров, среднего возраста работников (преподавателей, ученых, специалистов) и других аналогичных факторов растет риск вложения инвестиций.
Во втором случае с уменьшением (снижением) фактора риск инвестиций растет (Х2 и Х4). Например, с падением конкурентоспособности объектов (специалистов, менеджеров, технологии, оборудования, продукции, организации и т. д.), научного уровня принимаемых управленческих решений, средней заработной платы работников, фондовооруженности труда, социальной обеспеченности работников и других факторов аналогичного характера действия риск инвестиций растет.
Для использования этого инструмента управления рисками необходимо:
1) сделать отбор внешних и внутренних факторов риска, охватывающих макросреду, инфраструктуру региона и микросреду организации;
2) наладить мониторинг этих факторов;
3) проранжировать факторы с целью отбора важнейших из них (управлять или осуществлять мониторинг за всеми факторами невозможно);
4) установить форму связи между факторами и уровнем риска;
5) попытаться установить количественные зависимости (уравнения регрессии) между важнейшими факторами риска и уровнем риска;
6) определить эластичность между важнейшими факторами риска и уровнем риска вложения инвестиций.
Кроме выполнения этих исследований необходимо установить количественные зависимости между конечными показателями проекта (прибылью, доходностью, ликвидностью и др.) и уровнем риска. Например, зависимость между уровнем риска и прибылью (доходностью) от вложения инвестиций описывается кривой Y=f(Х3), риском и ликвидностью ценных бумаг кривой Y = f(X2),риском и устойчивостью функционирования организации функцией Y = f(X4)и т. д.
При оценке рисков следует рассчитывать вероятность достижения запланированного значения прибыли, которая описывается законом Гаусса (рис. 12.2). Для того чтобы управленческие решения в инновационных проектах находились в зоне «+» на рис. 12.2, необходимо исследовать влияние внешних и внутренних факторов риска на прибыль, снизить влияние негативных (повышающих риск) факторов на прибыль и оптимизировать уровень риска.
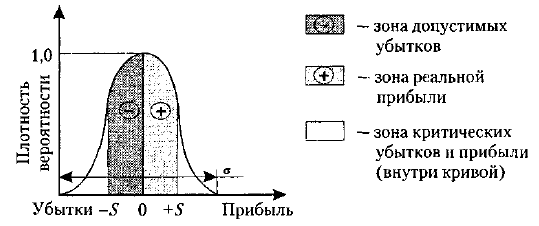
Рис. 12.2. Кривая распределения прибыли и убытков в зависимости от уровня риска
Поэтапная оптимизация риска представляет собой:
1) отбор и ранжирование факторов внешней и внутренней среды объекта и субъекта риска с применением методов факторного анализа (математико-статистические и экспертные);
2) установление зависимостей между отобранными факторами риска и объектом риска (доходом, прибылью и др.);
3) стохастическую оптимизацию риска.
Чем больше «S», тем выше риск прогнозируемого события, больше разброс, поле допуска (рис. 12.2) анализируемого параметра от средней величины (медианы, точка «0» на рис. 12.2), тем «грубее» модель оптимизации риска. Необходимо сглаживать, уменьшать факторы риска с тем, чтобы сузить поле «S», поле риска. Хорошо, когда «S» меньше ±15%.
Распределение результатов инноваций носит характер нормального распределения. Нормальное распределение (распределение Гаусса) – вид распределения случайных величин, с достаточной точностью описывающий распределение плотности вероятности результатов производственно-хозяйственной, финансовой, инновационной деятельности или изменений условий внешней среды, поскольку показатели, характеризующие их, определяются большим числом независимых случайных величин, каждая из которых в отдельности играет незначительную роль и непредсказуема. Эти теоретические предпосылки, а также апробация моделей для анализа рисков на основе нормального распределения доказывают адекватность этого теоретического инструмента реальным инновационным процессам:
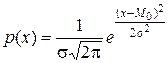 , (12.7)
, (12.7)
где Р(х) – плотность вероятности распределения случайной величины х; 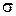 – дисперсия (рассеивание) случайной величины х; М0 – математическое ожидание.
– дисперсия (рассеивание) случайной величины х; М0 – математическое ожидание.
Нормальное распределение позволяет количественно оценить вероятность неблагоприятного значения:
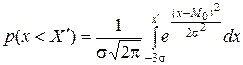 . (12.8)
. (12.8)
Если применение законов нормального распределения при анализе риска обеспечивает адекватность выводов и оценок, то на практике широко используется такой инструмент как Z-статистика. При анализе исходя из коэффициента Z оценивается вероятность того, что результат инновации окажется не хуже некоего критического уровня, определяемого инноватором или инвестором:
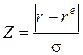 , (12.9)
, (12.9)
где r – критический уровень результата инновации.
По значению Z на основе табличных значений оценивается вероятность риска, если критический уровень превосходит среднее ожидаемое значение:
· r > rе, если инноватор заинтересован в максимизации результата;
· r < re, если инноватор заинтересован в минимизации результата.
Вероятность того, что результат нововведения превзойдет уровень хуже ожидаемого, оценивается по формуле:
Р = 1 - р, (12.10)
где р – значение вероятности, полученное по таблице.
Оценка вероятности риска может также производиться с помощью графиков, на которых по оси абсцисс (X) откладываются значения результатов инновации, а по оси ординат (Y) – плотности вероятности получения этих результатов.
При сравнении вариантов инновационных решений инноватор или инвестор предпочитает либо более высокодоходный вариант (более «правый график»), либо менее рисковый (менее «широкий график»).
Пример 4. Инвестор оценивает два инновационных проекта по критерию риска:
| Проект 1 | Доходность, % | -20 | -10 | |||
| Вероятность, % | ||||||
| Проект 2 | Доходность, % | -10 | -5 | |||
| Вероятность, % |
Наиболее вероятное значение доходности по проектам:
– проект 1: ((-20) 10+(-10) 20+5·30+15·30+20·10):100 = 4;
– проект 2: ((-10)·5+(-5)·20+O·50+5·20+10·5):100 = 0.
Дисперсия доходностей по проектам:
проект 1:
V((-20- 4)·10+ (-10- 4)·20 + (5- 4)·30+(15- 4)·30+(20- 4)·10 ):100 = 14
проект 2:
V((-10-0)·5+(-5- 0)·20+(0-0)·50+(5-0)·20+(10-0)·5):100 = 4
Риск убыточности проектов:
проект1: Z = (4 - 0):14 = 0,28 => р = 100 - 39 = 61%;
проект 2: Z = (0 - 0):4 = 0,0 => р = 50%.
39% < 50%, следовательно, второй проект сопряжен с меньшим риском.
Риск как экономическая категория совмещает в себе оценку вероятности неблагоприятного развития событий и меру этой неблагоприятности. Поэтому для описания риска используется двухмерная характеристика: степень и цена риска.
Степень риска количественно характеризует вероятность неблагоприятной динамики инновационного процесса и негативных результатов инновационной деятельности.
Цена риска отражает количественную оценку вероятного результата инновационной деятельности (показывает экономический результат, ради которого инвестор или инноватор пошел на риск).
Пример 5. Финансовому директору АО «Звезда» предстоит выбрать одно из двух альтернативных вложений временно свободных средств предприятия в размере 15 млн руб.:
· купить государственные ценные бумаги с гарантированной доходностью 3% годовых;
· разместить средства на депозите в коммерческом банке «Слава» под 5 % годовых.
Риск вложений в государственные бумаги составляет 1%, надежность банка оценивается рейтинговым агентством в 90%. Таким образом, степень риска операции с ценными бумагами составляет 1%, а депозитных операций – 10%.
Ожидаемый доход по государственным ценным бумагам за год составит 450 тыс. руб., а по депозитным операциям – 750 тыс. руб.
Цена риска вложений в ценные бумаги составляет:450·0,01 = 4,5 тыс. руб.
Цена риска размещения средств на депозите в банке составляет: 750·0,1 = = 75 тыс. руб.
Вкладывая деньги в банк и стремясь получить более высокий доход, финансовый директор должен иметь в виду, что его ожидаемые потери от этой операции значительно выше, чем от размещения средств в государственных ценных бумагах.
Мера риска показывает возможные потери либо в результате какой-либо производственно-хозяйственной или финансовой деятельности, либо вследствие неблагоприятного изменения состояния внешней среды (принятие решения мера риска может оцениваться либо как наиболее ожидаемый негативный результат, либо как пессимистическая оценка возможного результата). Если для описания риска адекватно применение нормального распределения (см. Z-статистика), то мера риска соответственно может оцениваться как математическое ожидание:
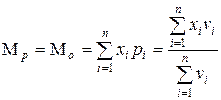 , (12.11)
, (12.11)
Мр – мера риска; Мо – наиболее ожидаемый результат (математическое ожидание); х – размер потерь в ходе i-го наблюдения; pj – вероятность возникновения потерь в результате i-го наблюдения; vi – число случаев наблюдения i-го результата; n – общее количество наблюдаемых результатов.
Пример 6. При изучении статистики освоения новой продукции были получены следующие данные:
| Группы проектов | Средняя сумма инвестиций, тыс.руб. | Число проектов | Число неудач |
| II |
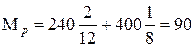 тыс. руб.
тыс. руб.
Принимая решение об освоении новой продукции, руководитель предприятия должен быть готов «потерять» в среднем 90 тыс. руб. на каждом новом типе изделий.
Если показатель меры риска используется как пессимистическая оценка результата, то применяется формула максимально возможного негативного отклонения – «три сигмы»:
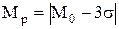 , (12.12)
, (12.12)
где σ – дисперсия.
Пример 7. Предварительная оценка результатов инновационного проекта создания консалтингового подразделения аудиторской компании показала, что наиболее ожидаемый доход от этой инновации составит 700 тыс. руб., но точность расчетов (стандартное отклонение, колеблемость) составляет 40%.
Тогда среднее линейное отклонение (а) составляет:
а = 700 * 40% / 100% = 280 тыс. руб.
 Мера риска в данном случае оценивается как возможный убыток деятельности консалтингового подразделения фирмы:
Мера риска в данном случае оценивается как возможный убыток деятельности консалтингового подразделения фирмы:
Мр = |700 - 3·280 = 140 тыс. руб.
Убыток не превысит 140 тыс. руб.
Однако мера риска может быть менее Мо– 3σ; если максимальные потери реально менее расчетного значения, то мера риска совпадает с максимальными потерями в результате реализации инновационного проекта.
Пример 8. Мера риска для проекта организации выпуска витаминов – 20 тыс. руб., поскольку именно эту сумму инновационная фирма затратила на исследования и разработки, хотя по расчетам максимальное негативное отклонение составляет: Мр= ׀10 – З· 21׀ = 51 тыс. руб.
Но такая сумма потерь в данном случае нереальна, поэтому в качестве меры риска принимается размер инвестиций, вложенных в реализацию проекта.
При принятии решения в области управления риска часто используются кумулятивные статистические кривые (графики Лоренца, рис. 10.1), на которых накопленным итогом отражается вероятность неблагоприятной ситуации в зависимости от оценки неблагоприятности.
Зоны риска
Инновации, обеспечивающие рентабельность не ниже расчетной, считаются безрисковой областью, которая не рассматривается как объект риск-менеджмента [78].
Частота операций, убытки которой были компенсированы другими операциями, включает также статистику по операциям, доходность которых была ниже расчетного уровня. Эти кумулятивные показатели позволяют определить зоны риска.
Зоны риска – качественная характеристика степени риска в зависимости от вероятности его возникновения. Для определения зон риска обычно используется кривая Лоренца, построенная по кумулятивным данным. Как правило, выделяют следующие зоны риска:
I. зона допустимого риска: возникновение рисковой ситуации не приводит к существенному ухудшению финансового положения компании);
II. зона умеренного риска: убытки от возникновения рискового события покрываются прибылью других областей деятельности;
III. зона высокого риска: в результате возникновения рисковой ситуации ухудшается финансовое положение компании;
IV. зона недопустимого риска: рисковое событие приводит к неплатежеспособности или банкротству предприятия.
 В противоположность зонам рискам выделяют безрисковую зону, где существует возможность не наступления рискового события. Безрисковая зона является характеристикой шанса.
В противоположность зонам рискам выделяют безрисковую зону, где существует возможность не наступления рискового события. Безрисковая зона является характеристикой шанса.
Для оценки рисков и разработки методов управления ими часто используют графики Лоренца (рис. 12.3). График строится как сглаженная кривая по фактическим данным накопленного риска. Как правило, эта кривая располагается ниже прямой, соединяющей крайние точки графика, то есть является выпуклой вниз. В этом случае риск растет более высокими темпами, чем полезность данной области инновационной активности. Уровень рискованности оценивается по коэффициенту кривизны, интерпретируемому как коэффициент риска (К рска) (рис. 12.3) [81]:
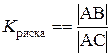 , (12.3)
, (12.3)
где АВ – отрезок диагонали до кривой Лоренца; АС – отрезок диагонали до другой диагонали.

| I | II | III | IV |
| Линия | |||
| равенства | |||
Рис. 12.3. Зоны риска по графику Лоренца
Чем больше коэффициент риска, тем более рискованным является данным вид деятельности. Однако возможна и ситуация, при которой кривая является выпуклой вверх. В этом случае считается, что риск деятельности растет медленнее, чем полезность данной области инновационной активности. Кривые Лоренца служат основанием для определения стратегии управления рисками.
Пример 9. Результаты внедрения технологических инноваций на опытном заводе «Пионер» характеризовались следующими данными (число инноваций, реализованных с различной эффективностью).
| Год | Рентабельность не ниже расчетной | Рентабельность ниже расчетной | Убыточность, компенсироанная займами и внешним финансированием | Убыточность, компенсированная доходностью от прочих операций | Непокрытая убыточность |
| Итого | |||||
| % | 40,9% | 33,7% | 15,9% | 12,5% | 8,0% |
В данном примере зоны риска определяются следующим образом:
· рентабельность не ниже расчетной – безрисковая область (40,9%);
· рентабельность ниже расчетной – зона допустимого риска (22,7%);
· убыточность, компенсированная доходностью от прочих операций - зона умеренного риска (38,6%);
· убыточность, компенсированная займами и внешним финансированием - зона высокого риска (51,1%);
· непокрытая убыточность – зона недопустимого риска (59,1%).
Для оценки риска по остальным группам можно рассчитать кумулятивные вероятности, считая, что наименее плохой результат автоматически включает в себя и более неблагоприятный исход (табл. 12.2)
Таблица 12.2. Кумулятивные вероятности по группами риска (%)
| Рентабельность не ниже расчетной | Рентабельность ниже расчетной | Убыточность, Компенсироанная займами и внешним финансированием | Убыточность, компенсированная доходностью от прочих операций | Непокрытая убыточность |
| 40,9% | 22,7 | 15,9 | 12,5 | 8,0 |
| 40,9% | 22,7 | 38,6 | 51,1 | 59,1 |
Дата добавления: 2017-06-02; просмотров: 5002;
