Нечеткое множество и нечеткое отношение

Рассмотрим универсальное множество 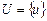. Нечетким множеством А на множестве U называется совокупность пар

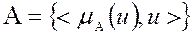, (1.3)

где 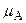: 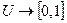— отображение множества U в единичный отрезок [0, 1], называемое функцией принадлежности нечеткого множества А.Значение функции принадлежности 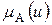для элемента 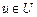будем называть степенью принадлежности. Для упрощения записи будем считать, что выражению (1.3) эквивалентны выражения

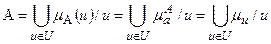(1.4)

Переменная и называется базовой. Верхний индекс в (1.4) будем опускать там, где это не приведет к неоднозначности.

Точки 0 и 1 представляют собой соответственно низшую и высшую степень принадлежности элемента к определенному подмножеству.

Точкой переходанечеткого множества А называется элемент u множества U, для которого 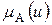=0.5.

Интерпретацией степени принадлежности 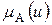является субъективная мера того, насколько элемент 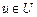соответствует понятию, смысл которого формализуется нечетким множеством А. Другими словами "величина 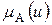обозначает субъективную оценку степени принадлежности u к множеству А, например 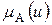=0,8 означает, что u на 80% принадлежит А". Следовательно, могут существовать "моя функция принадлежности", "твоя функция принадлежности", "функция принадлежности эксперта".

Функция принадлежности, во-первых, имеет субъективный характер и, во-вторых, может интерпретироваться на основе понятия вероятности. В рамках вероятностной трактовки значение 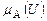функции принадлежности нечеткого множества А для любого элемента 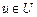понимается как вероятность того, что ЛПР отнесет элемент uк множеству А. Данная интерпретация позволяет установить, с каким объектом «работают» теория нечетких множеств и базирующийся на ней лингвистический подход к обработке неопределенной информации.

Поскольку до недавнего времени практически единственным средством формализации неопределенной информации являлась теория вероятностей, важно отметить, что объектом теории нечетких множеств не является функция плотности вероятности или функция распределения. Это связано, в частности, с тем, что для первой обязательно условие нормировки

,

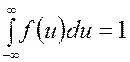а для второй — свойство не убывания на отрезке [0, 1]. Как первое, так и второе свойства не обязательны для функции принадлежности по ее определению. Таким образом, требуется специальный аппарат, который позволял бы обрабатывать информацию, формализованную с помощью нечетких множеств.

Носителем нечеткого множества А называется множество

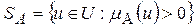. (1.5)

Иными словами, носителем нечеткого множества А является подмножество S_A универсального множества Х, для элементов которого функция принадлежности μ_A строго больше нуля.

В качестве примера рассмотрим нечеткое множество А₃, соответствующее нечеткому понятию «небольшой запас деталей на складе». Носителем данного нечеткого множества является конечное множество S{10, 11, …, 40}, каждый элемент которого представляет собой определенное количество деталей.

А₃={0,05/10; 0,1/11; 0,2/12; 0,3/13; 0,4/14; 0,5/15; 0,7/16; 0,8/19; 1,0/20; 1,0/21;…; 1,0/33; 0,9/0,34; 0,8/35; 0,6/36; 0,4/37; 0,3/38; 0,2/39; 0,1/40}.

Отсюда следует, что в решаемой задаче управления запасами для конкретного ЛПР понятию «небольшой запас деталей на складе» полностью соответствует запас объемом от 20 до 33 деталей, в меньшей степени – запасы от 11 до 19 и от 34 до 40 деталей. Запас объемом меньше 10 и больше 40 деталей понятием «небольшой» охарактеризован быть не может.

Для практических приложений носители нечетких множеств всегда ограничены. Так, носителем нечеткого множества допустимых режимов для системы может служить четкое подмножество (интервал), для которого степень допустимости не равна нулю (рис.1.2).

Рис.1.2. Понятие носителя нечеткого множества (выделен жирной чертой)

Высотой d нечеткого множества А называется максимальное значение функции принадлежности этого множества .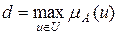

Если d = 1, то нечеткое множество называется нормальным.

Ниже будут рассматриваться только нормальные нечеткие множества, так как если нечеткое множество не нормально, то его всегда можно превратить в нормальное, разделив все значения функции принадлежности на ее максимальное значение.

Пусть 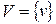– другое универсальное множество. Нечетким отношением R на множестве 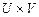называется совокупность пар

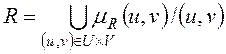, (1.6)

где 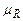: 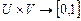– функция принадлежности нечеткого отношения R, имеющая тот же смысл, что и функция принадлежности нечеткого множества. Приведенное определение легко обобщается на n-мерный случай.

Сравнивая выражения (1.3) и (1.6), можно видеть, что нечеткое отношение – это нечеткое множество с векторной базовой переменной. Примерами нечетких отношений могут служить такие, как «X примерно равен У», «X значительно больше У», «А существенно предпочтительнее, чем В».