Что такое нечеткие множества?

В классической математике мы хорошо знакомы с тем, что мы называем четкие множества. В обычной теории множеств существуют несколько способов задания множества. Одним из них является задание с помощью характеристической функции, определяемой так. Пусть U - универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в настоящей задаче, например множество всех целых чисел, множество всех гладких функций, заданных на действительной оси, и т.д. В дальнейшем в качестве универсального множества будет, как правило, использовано множество всех действительных чисел. Характеристическая функция множества - это функция, значения которой указывают, является ли Х элементом множества A. Особенностью этой функции является бинарный характер ее значений, т.е. 1 или 0.

Рассмотрим, например множество X всех вещественных чисел между 0 и 10, которые будем называть предметной областью.

Определим подмножество A из X всех вещественных чисел в диапазоне между 5 и 8. A = [5,8]. Покажем множество А в виде характеристической функции, то есть эта функция присваивает значение 1 или 0 каждому элементу в X, в зависимости от того, находится ли элемент в подмножестве или нет (рисунок 1).

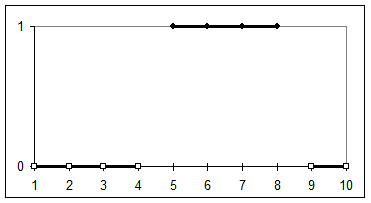
Рисунок 1 – Пример характеристической функции четкого множества

Другими словами, если характеристическая функция элементов, равна 1, то эти элементы, принадлежат множеству A, а элементы, у которых характеристическая функция равна 0 - не принадлежат множеству A.

Это понятие применимо для достаточно многих областей приложений. Но мы можем легко найти ситуации, где этот метод испытывает недостаток в гибкости.

Например, рассмотрим множество молодежи. Формально обозначим:

B = {множество молодежи}.

Так как возраст начинается с 0 лет, то отрицательный диапазон этого набора должен быть пуст. Верхнюю границу диапазона определить довольно трудно. Для начала мы установим верхнюю границу диапазон, например, 20 лет. Следовательно, мы получаем B как четкий интервал: B = [0,20] .

Теперь возникает вопрос: почему кто-то на его 20-ом дне рождения молодой, а на следующий день не молодой? Очевидно, это - структурная проблема, поскольку, если мы возьмем другой интервал от 20 до любой произвольной отметки, мы можем задать тот же самый вопрос.

Более естественный способ задавать набор B состоит в том, чтобы ослабить строгое разделение между понятиями молодой и не молодой. Мы может делать это, позволяя не только (четкое) решение "ДА, он/она находится в наборе молодежи, или НЕТ, он/она не находится в наборе молодежи", но и применяя более гибкие фразы, например, "он/она принадлежит немного больше к набору молодежи или НЕТ, он/она почти не принадлежит к набору молодежи".

Рассмотрим формальное описание данной идеи. Прямой способ обобщить это понятие состоит в том, чтобы учитывать больше значений между 0 и 1. Фактически возможны многие варианты между 0 и 1, а именно числовой интервал I = [0, 1].

Интерпретация чисел (см. рисунок 1), назначенных теперь ко всем элементам предметной области более трудна. Конечно, снова 1 присвоенная элементу означает, что элемент находится во множестве B, а 0 - что элемент не определен во множестве B. Все другие значения означают частичную принадлежность к множеству B.

Реализацию данной идеи рассмотрим на примере множество молодежи. На рисунке 2 изображена характеристическая функция.

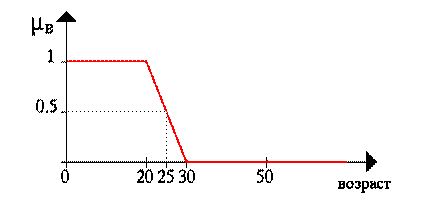
Рисунок 2 – Характеристическая функция множества молодежи

Из рисунка 2 видно, что в 25 лет вы все еще молоды, но не на все 100%, а всего на 50.