Вид износа режущего инструмента и способы устранения этого износа
| Вид износа | Способы устранения | ||||||
| Уменьшить скорость резания | Увеличить скорость резания | Умень- шить подачу | Уменьшить глубину резания | Выбрать более износостойкую марку сплава | Выбрать более прочную марку сплава | Выбрать режущую пластину с положительной геометрией | |
| Износ по задней поверхности | + | + | |||||
| Образование проточин | + | + | |||||
| Лункообразование по передней | + | + | + | + | |||
| поверхности | |||||||
| Пластическая деформация | + | + | + | ||||
| Наростообразование | + | + | |||||
| Термические трещины | + | ||||||
| Выкрашивание | + | + | + | ||||
| Поломка пластины | + | + | + |
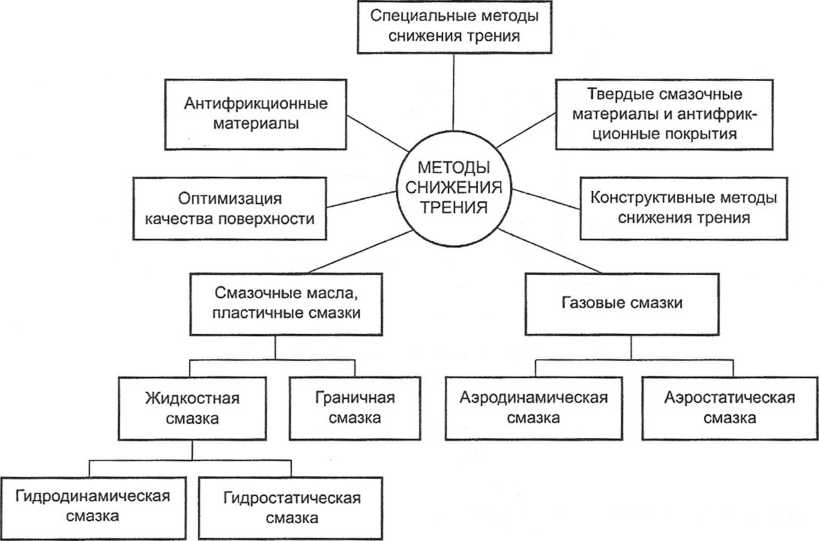
34. ПУТИ СНИЖЕНИЯ ТРЕНИЯ
|
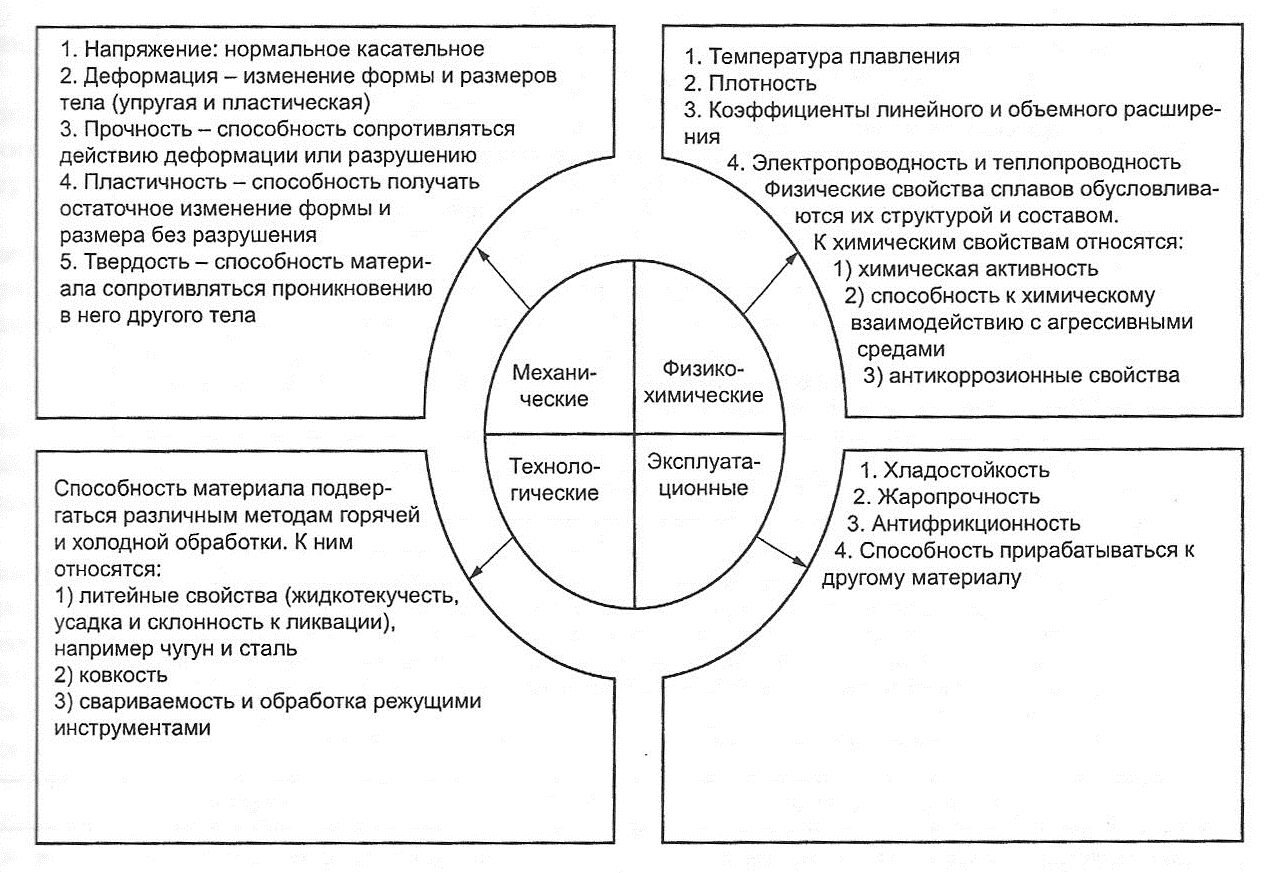
36. СТРОЕНИЕ ПОАЕРХНОСТНОГО СЛОЯ МЕТАЛЛА
| Граничный слой |
| Атомы имеют связи только с соседними и нижележащими атомами и находятся в неуравновешенном неустойчивом состоянии. Граничный слой, включающий примерно два ряда атомов (10'6 - 10'7 мм) обладает запасом свободной поверхностной энергии, вследствие чего адсорбирует элементы окружающей среды (газы, пары воды и жиры). Адсорбция снижает поверхностную энергию и облегчает развитие деформаций, приводит к возникновению химических соединений. Общая толщина наружной пленки составляет: в стали 1,0- 2,0 нм, в железе 1,5 - 2,5 нм; 1 нм (нанометр) = 10'9 м |
| Поверхностный слой металла включает в себя наружную поверхность (граничный слой) и слой деформированного металла, отличающегося от основной части (сердцевины) по своим механическим, физическим и химическим свойствам |
| Внутренняя часть поверхностного слоя |
| У металлов (в ненапряженном ионном состоянии) располагаются поликристаллические структуры размерами от 0,01 до 1,0 мм, связанные межзеренной прослойкой, имеющей искаженную кристаллическую решетку с дислоцированными атомами основного материала и примесей. Строение прослойки характеризуется ослабленными силами сцепления и повышенной энергией атомов. Толщина межзеренных слоев составляет около 5-20 атомных слоев |
| Мозаичная структура (МС) |
| Дислокации |
| При кристаллизации формируется так называемая МС с размерами 10‘3 - 10^ мм (т.е. до 100 000 атомных расстояний) неправильной формы, но правильного внутреннего строения. Блоки мозаики - мелкие кристаллы; наименьший кристаллит, обнаруженный рентгеновским методом, имел размер 1,8 нм и состоял из 100 элементарных ячеек, включающих 400 атомов. В 1 мм3 может находиться до 1012 блоков. В кристаллитах всегда существуют атомы, обладающие энергией превосходящей среднее значение соседних атомов, поэтому они покидают свои места равновесия, создавая в них пустоты (вакансии). Возникновение вакансий изменяет плотность металла. Точечные дефекты (вакансии, примеси, пустоты и дислоцированные атомы) существенно влияют на механические, химические, оптические и магнитные свойства металлов |
| Дислокации представляют собой более сложный дефект структуры, чем любой из точечных дефектов. Возможные типы несовершенства кристаллической структуры состоят из краевой и винтовой дислокаций. Формирование краевой дислокации вызвано тем, что в часть объема кристалла введена лишняя атомная плоскость. Винтовая дислокация заключается в новом характере атомных плоскостей, перпендикулярных к дислокации. Все атомы находятся на одной поверхности, эта поверхность является винтовой; она начинается у одного края кристалла и заканчивается у другого. Дислокации, как точечные дефекты, могут переме-щаться по кристаллической решетке. Механическая прочность твердых тел зависит, главным образом, от дислокаций. Значительные расхождения теоретической и фактической прочности металлов объясняются наличием в реальных поликристаллах различных несовершенств и дефектов кристаллической решетки. Причина увеличения напряжения состоит в том, что в процессе деформации сильно возрастает количество дислокаций. В результате дислокации начинают хаотически переплетаться друг с другом. Это явление называется наклепом (один из типичных методов получения прочного материала) |
37. СХЕМА ПОВЕРХНОСТНОГО СЛОЯ МЕТАЛЛА
Зона 1 - адсорбированная пленка газов, влаги и смазочно-охлаждающей жидкости, которая удаляется нагревом детали в вакууме.
Зона 2 - деформированный, сильно раздробленный металл с искаженной решеткой кристаллов и с обезуглероженными под действием высоких температур при шлифовании участками; в нем находятся оксиды и нитриды, пустоты и надрывы, а также трещины.
Зона 3 - зерна, сильно деформированные под действием давления 3 шлифовального круга и тангенциальных сил при шлифовании; в зоне содержатся структуры свободного цементита, образовавшегося под действием высоких температур.
Зола 4 - металл с исходной структурой (рис. 37.1).
В технике поверхность детали - наружный слой, который по строению и другим свойствам отличается от внутренней части. Комплекс свойств, приобретаемых поверхностью детали в результате ее обработки, характеризуется обобщенным понятием «качество поверхности».
Качество поверхности характеризуется геометрией (макро-, микрогеометрией и волнистостью); физико-механическими и физико-химическими свойствами. Указанные характеристики качества поверхности влияют на такие служебные свойства деталей, как сопротивление усталости, износо-, коррозие- и эрозиостойкость, и связан со свойствами сопряжения, прочности посадок с натягом, плотности подвижных и неподвижных соединений.
Физико-механические свойства поверхностного слоя определяются твердостью; структурными и фазовыми превращениями; величиной, знаком и глубиной распространения остаточных напряжений; деформацией кристаллической решетки. Эти свойства в основном определяются упру- го-пластическим деформированием и местным нагревом зоны обработки.
Физико-химические свойства поверхности характеризуются наличием на металлической поверхности различных пленок, прочно связанных с основным металлом. Формирование физикохимических свойств поверхностного слоя, в частности адсорбционной и оксидной пленок, вызвано физическим и химическим взаимодействием обрабатываемого металла в зоне резания с окружающей средой.
Погрешности обработанной поверхности с точки зрения их образования и методов измерительной техники, применяемых для их определения, подразделяются на три категории: макрогео- метрические отклонения, волнистость, шероховатость поверхности.
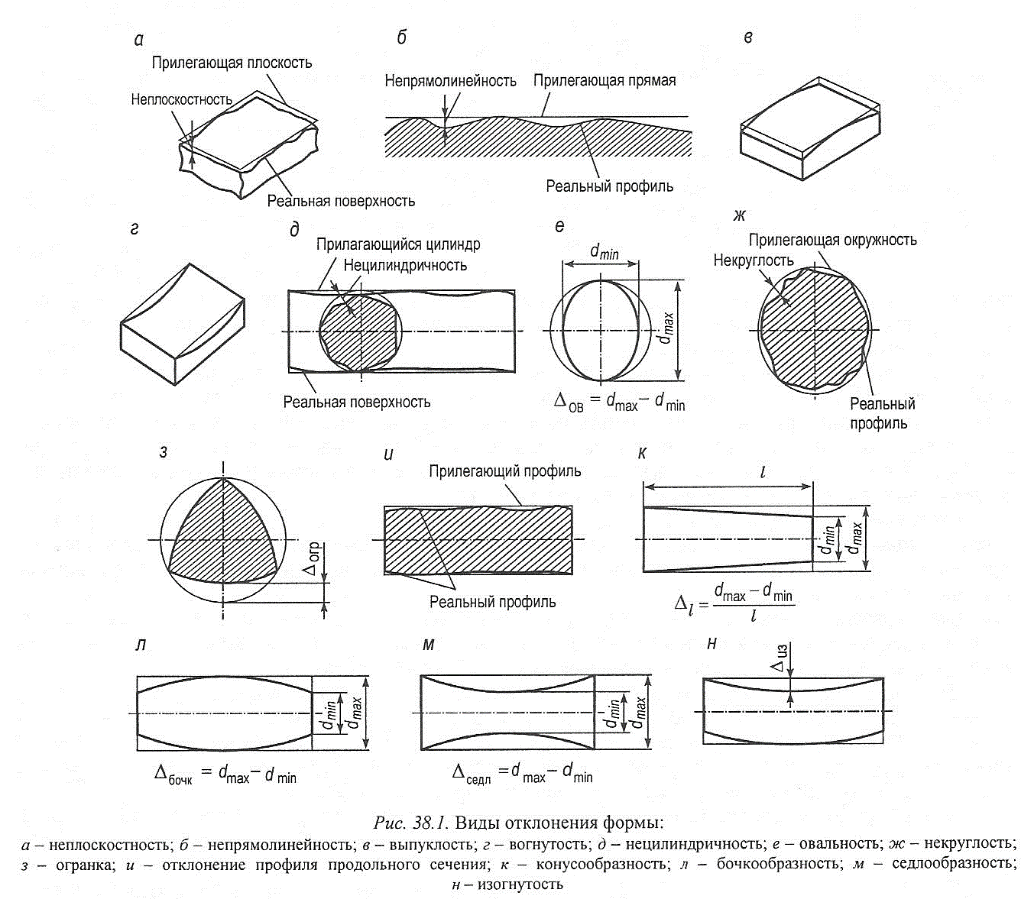
Макрогеометрические отклонения.В общем случае поверхность предмета - это граница, которая отделяет данный предмет от другого предмета или окружающей среды. Можно выделить несколько критериев оценки поверхности. Различают реальную (действительную), измеренную и номинальную (теоретическую) поверхность.
Реальную {действительную) поверхность в общем случае можно описать функцией от двух независимых переменных.
Измеренную поверхность можно определить с помощью измерительных устройств.
Номинальная (теоретическая) поверхность задается чертежом либо описывается с помощью математических уравнений.
Номинальная поверхность характеризуется отклонениями формы, волнистостью и шероховатостью. Среди отклонений формы можно выделить, например, различные виды отклонений от круглости (овальность, огранка), цилиндричности, плоскостности и т.д. согласно ГОСТ 24642-81.
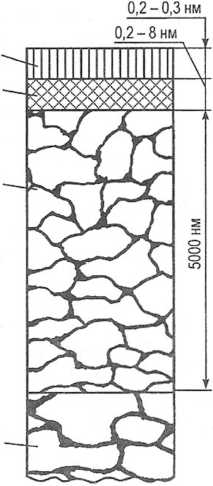
Рис.37.1.Схема строения поверхностного слоя
Причины: неточность станка, погрешности установки заготовки; силовые и температурные деформации системы «станок - приспособление - инструмент - заготовка» и износ инструмента.
Волнистость поверхности.Волнистость поверхности совокупность периодически повторяющихся неровностей, у которых расстояние между смежными возвышенностями или впадинами превышают базовую длину / (/ = 0,08 - 8,0 мм). Волнистость занимает промежуточное положение между макрогеометрическими погрешностями (отклонениями формы) и шероховатостью поверхности.
Волнистость поверхности образуется в результате неравномерности подачи при точении и шлифовании, неплоскостности направляющих и вынужденных колебаниях системы «станок - заготовка - инструмент», возникающих из-за неравномерности сил резания, наличия неуравновешенных масс, копирования волнистости режущего инструмента, искажения формы шлифовального круга и неравномерный износ его, а также погрешности движения инструмента или заготовки.
При шлифовании сильно сказывается дисбаланс круга. При зубофрезеровании ошибка червяка делительной передачи станка проявляется в виде волнистой боковой поверхности зуба.
От шероховатости волнистость отличается значительно большим шагом; при чистовой обработке он не менее 0,25 мм, при черновой - превышает 8 мм. Нередко бывает, что высота волны при чистовом точении и цилиндрическом шлифовании доходит до 15 мкм при шаге до 14 мм.
Действующими рекомендациями установлены следующие параметры волнистости. Высота волнистости W. - среднее арифметическое из пяти ее значений (Wb W2,..., W5), определенных на участке измерения Lw, равном не менее пяти действительным наибольшим шагам волнистости (рис. 37.2, а):
Wz =  (Wl+W2+W3+W4+W5).
(Wl+W2+W3+W4+W5).
Допускается непоследовательное расположение участков измерения. Числовые предельные значения Wz нужно выбирать из ряда: 0,1; 0,2; 0,4; 0,8; 1,6; 3,2; 6,3; 12,5; 25; 50; 100; 200 мкм. Отдельные измерения волнистости производят на длине lw\ равной пятой части Lw.
Наибольшая высота волнистости JVmax - расстояние между наивысшей и наинизшей точками измеренного профиля в пределах Lw, измеренное на одной полной волне.
Средний шаг волнистости Sw - среднее арифметическое значение длин отрезков средней линии SiVh ограниченных точками их пересечения с соседними участками профиля волнистости (рис. 37.2, б):
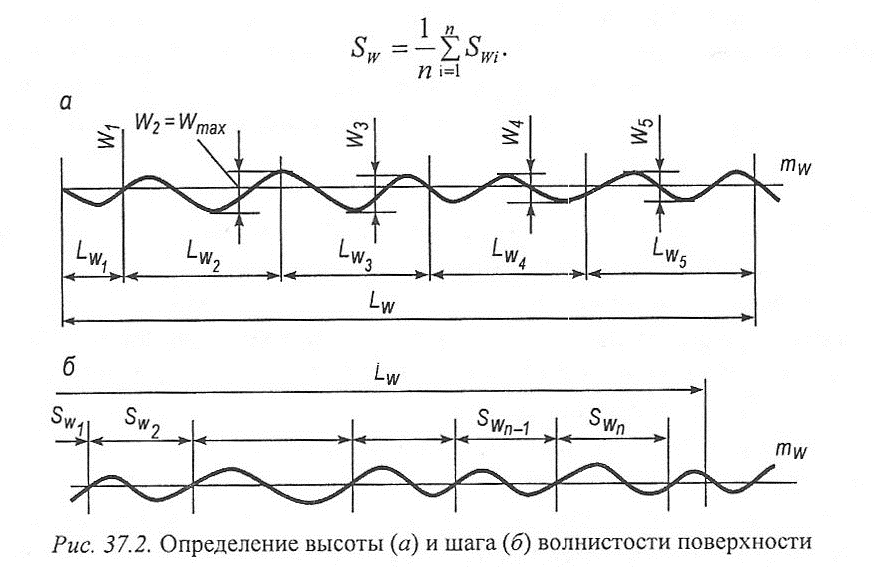
Положение средней линии mw определяется так же, как и средней линии профиля т шероховатости.
Форма волны может быть различной в зависимости от причин, которые вызывают волнистость поверхности. Чаще всего волнистость имеет синусоидальный характер.
38. ОТКЛОНЕНИЯ ФОРМЫ (МАКРООТКЛОНЕНИЯ)
39. ШЕРОХОВАОСТЬ ПОВЕРХНОСТИ
Реальная поверхность не является гладкой, она имеет неровности: выступы и впадины с относительно малым расстоянием между ними. Под шероховатостью поверхности понимают совокупность неровностей поверхности с относительно малыми шагами на базовой длине /. Иногда сочетание выступов и впадин реальной поверхности называют микрорельефом поверхности.
Контур сечения реальной поверхности плоскостью, перпендикулярной соответствующей идеальной геометрической поверхности, образует профиль, характеризующий микрогеометрию поверхности изделия.
Графическое изображение реального профиля по данным измерений шероховатости, называют профилограммой шероховатости. Так как через данную точку геометрической поверхности
можно провести бесконечное множество нормальных сечений, то шероховатость поверхности следует связывать с тем или иным направлением.
Причины образования шероховатости (рис. 39.1, а, б) - возникновение нароста на режущем лезвии, параметры режима обработки, геометрия режущего инструмента, жесткость технологической системы (упругие деформации), наличие или отсутствие смазочно-охлаждающей жидкости (СОЖ).
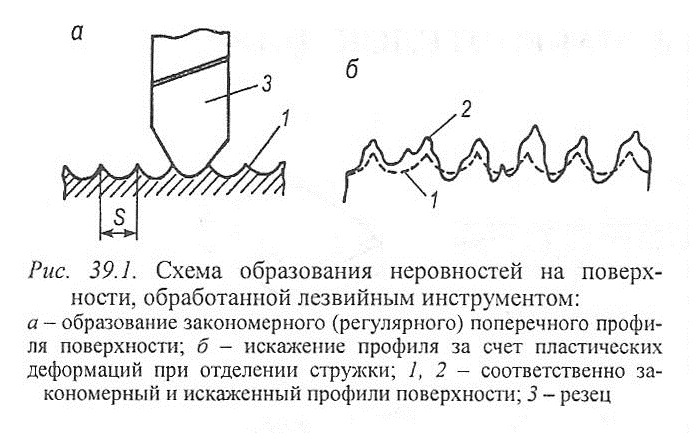
Шероховатость обработанной поверхности является следствием пластической деформации поверхностного слоя детали при образовании стружки, копирования неровностей режущих кромок инструмента и трения его о заготовку, вырывания с поверхности частиц материала и других причин. Обработанную резанием поверхность можно в первом (грубом) приближении рассматривать как след режущей кромки инструмента. При строгании форма режущей кромки и перемещение образца в конце каждого холостого хода на величину подачи определяют шероховатость поверхности - образование рисок в направлении, перпендикулярном возвратно-поступательному движению стола. Зазубрины на режущей кромке резца создают шероховатость во впадинах между гребешками. При точении след режущей кромки представляет собой винтовую линию поверхности с шагом, равным подаче резца за один оборот заготовки.
Шероховатость обработанной поверхности в направлении главного движения при резании именуют продольной, а в направлении подачи - поперечной шероховатостью. Преобладающее направление следов механической обработки поверхности или следов трения называют направлением неровностей.
Шероховатость поверхности — размерная характеристика поверхности. Количественно ее можно определить по тем или иным показателям. При этом следует иметь в виду, что количественно шероховатость устанавливают независимо от способа ее обработки.
Для оценки используют действующий в настоящее время комплект Международных норм, характеризующих геометрическую структуру обработанной поверхности - ISO-3274:1997 и ISO-4287:1998. Под этим понимается объединение всех неровностей поверхности. Наиболее часто она анализируется в сечении, перпендикулярном к поверхности. При наличии ярко выраженных следов обработки используется сечение, перпендикулярное таким следам.
Общий профиль поверхности в поперечном сечении может быть разделен на профили формы, волнистости и шероховатости. Согласно нормам ISO, первая буква в обозначении параметров профиля поверхности характеризует тип профиля: Р (primary) - первичный (действительный) профиль; W (waviness) - профиль волнистости; R (roughness) - профиль шероховатости.
При рассмотрении параметров профиля поверхности принята следующая система определения общих понятий (рис. 39.2):
•профиль поверхности - профиль, полученный в результате пересечения этой поверхности заданной плоскостью;
•теоретический профиль (traced profile) - геометрическое место точек середины вершин формирующего лезвия идеальной геометрической формы (закругленный конус) и соответствующих размеров, перемещающегося по поверхности, в заданной плоскости;

•измеренный профиль {reference profile) - профиль, зарегистрированный при перемещении датчика вдоль измеряемой поверхности;
•общий профиль (total profile) - цифровое сопоставление теоретического и измеренного профилей с общим расположением вертикальной и горизонтальной координат;
•фильтр профиля {profile filter) - фильтр, разделяющий коротковолновые и длинноволновые профили поверхности;
•фильтр профиля {profile filter) λg - фильтр, определяющий переход от шероховатости (микронеровностей) к еще меньшим длинам волн, сформированным на исследуемой поверхности;
•фильтр профиля {profile filter) λс - фильтр, определяющий переход от шероховатости к волнистости;
•фильтр профиля {profile filter) λf- фильтр, определяющий переход от волнистости к еще более большим неровностям на поверхности;
•первичный профиль {primary profile) - полный профиль после использования фильтра λg, отделяющего составляющие с длиной волны меньшей, чем у шероховатости;
•профиль шероховатости {roughness profile) - профиль, генерированный из первичного профиля в результате отделения составляющих с большими длинами волн фильтром λc;
•профиль волнистости {waviness profile) - профиль, генерированный из первичного профиля при использовании фильтра λс, отделяющего коротковолновые составляющие профиля (шероховатость), и фильтра λf, отделяющего составляющие с большими длинами волн;
•элементарный отрезок {samling length) Ip (первичного профиля), lr (профиля шероховатости), lw (профиля волнистости) - длина отрезка средней линии, предназначенная для оценки неровностей, характеризующих данный профиль;
•длина оценки {evaluation length) In - длина отрезка средней линии, использованная для оценки профиля;
•длина измерения {totaltraverse length) -полная длина отрезка профиля, измеренная прибором;
•средняя линия первичного профиля {mean line the primary profile) - линия, образованная при приближении номинального и первичного профилей методом наименьших квадратов;
•средняя линия профиля шероховатости {mean line the roughness profile) - линия, соответствующая длинноволновым составляющим профиля, которые гасит фильтр λc;
•средняя линия профиля волнистости {mean line the waviness profile) - линия, соответствующая длинноволновым составляющим профиля, которые гасит фильтр λf,
•выступ (впадина) профиля {mean peak, profile valley) - часть оцениваемого профиля, обращенная наружу (внутрь) материала, соединяющая соседние точки пересечения профиля со средней линией;
•элемент профиля {profile element) - выступ и прилегающая к нему впадина профиля;
•текущая высота профиля {ordinate value) Z{x) - высота измеряемого профиля для заданной горизонтальной координаты х (рис. 39.3);
•местный наклон профиля {local slope) dZ(x)/dx- наклон измеряемого профиля в рассматриваемой точке х;
•максимальная высота вершин профиля {profile peak heigth) Zp - расстояние между наивысшей вершиной профиля и средней линией;
•наибольшая глубина впадин профиля {profile valley depta) Zv - расстояние между наинизшей впадиной профиля и средней линией;
•перепад высот профиля {profil element height) Zt - сумма высоты вершины и глубины впадины для одного элемента профиля.
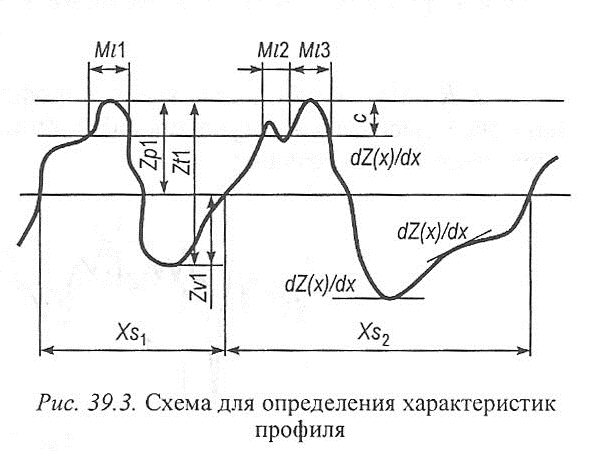
•ширина элемента профиля Xs - длина отрезка средней линии, ограниченная контуром элемента профиля;
•длина материала элемента профиля на уровне с, МI(с) - сумма измеренных длин отрезков, образованных в результате пересечения элемента профиля линией, параллельной средней линии на заданном уровне с.
Высотные характеристики профиля (рис. 39.4) - это характеристики, определяемые на основании сведений о высотах профиля в соответствующих точках длины профиля.
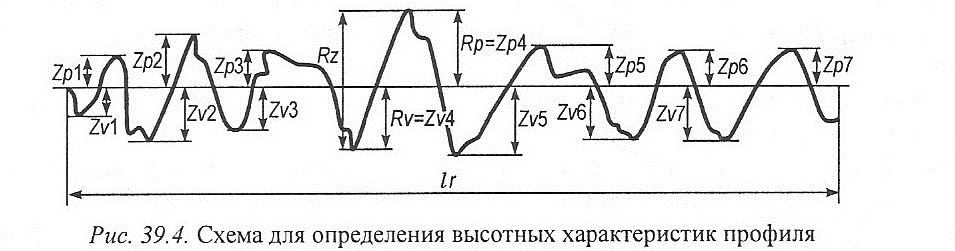
Рр, Rp, Wp — высота наиболее высокого выступа профиля {maximum profile peak height) Zp внутри элементарного отрезка lr:
Rp = (Rp 1 +Rp2 + Rp3 + Rp4 + Rp5)/5.
Pv, Rv, Wv - глубина наиболее низкой впадины профиля (maximum profile valley depta) Zv внутри элементарного отрезка Ir:
Rv = (Rv 1 + Rv 2 + Rv 3 + Rv 4 + Rv5)/5.
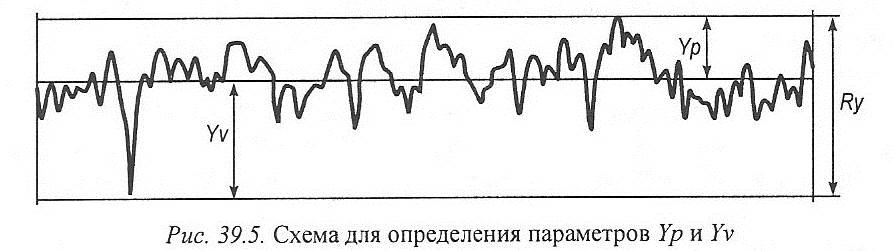
Максимальная высота профиля Ry - сумма высоты Yp наиболее высокого выступа профиля относительно средней линии и глубины наиболее глубокой впадины Yv относительно средней линии (рис. 39.5):
Ry = Yp+ Yv.
Общая высота профиля Rt - сумма максимальной высоты выступов профиля и максимальной глубины профиля на полном отрезке измерения:
Rt = Rp + Rv.
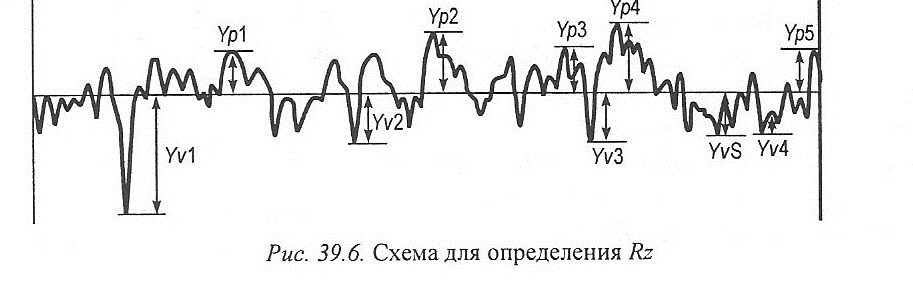
Pz, Rz, Wz - наибольшая высота профиля (maximum height of profile) (рис. 39.6) - сумма высоты наиболее высокого выступа профиля Zp и глубины наиболее низкой впадины профиля Zv внутри элементарного отрезка Ir.
Pc, Rc, Wc - средняя высота элементов профиля {mean height of profile elements) Zt внутри эле-ментарного отрезка Ir:
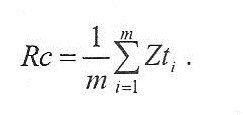
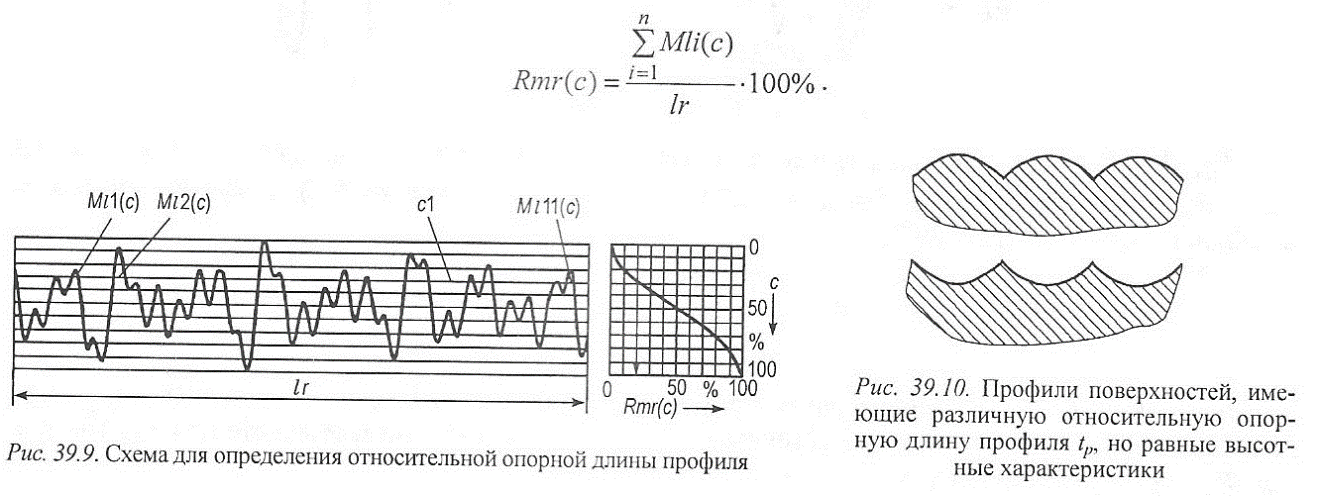
Pt, Rt, Wt - общая высота профиля {total height of profile) - сумма высоты наиболее высокого выступа профиля Zp и глубины наиболее низкой впадины профиля Zv внутри длины измерения In; кривая длины материального профиля {material ratio of the profile) - это кривая, представляющая собой долю материала в данном сечении как функцию высоты сечения P§c,Rbc,Wbc {profile section height difference) - разница между двумя долями материала на двух заданных уровнях сечений:
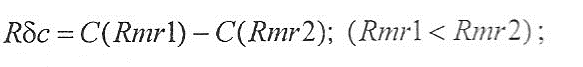
Pmr, Rmr, Wmr - относительная доля материала {relative material ratio) - доля материала профиля, измеряемая на уровне сечения с высотой С и на расстоянии Rδc:
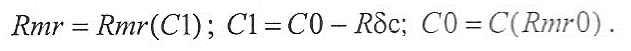
Pa, Ra, Wa - средняя арифметическая высота профиля {arithemical mean deviation of the assessed profile) - средняя арифметическая абсолютных значений высот Z(x) профиля внутри элементарного отрезка Ir;
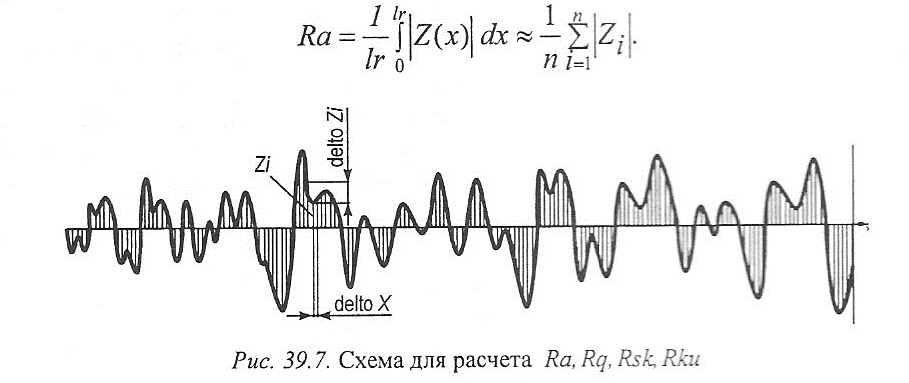
Pq, Rq, Wq- средняя квадратическая высота профиля {root mean square deviation form the assessed profile) - средняя квадратическая абсолютных значений высот Z(x) профиля внутри элементарного отрезка Ir (рис. 39.7):
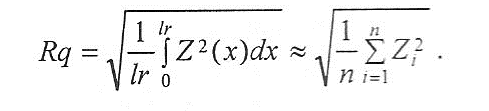
Psk, Rsk, Wsk - коэффициент асимметрии профиля {skewness of the assessed profile) - произведение третьей степени средних значений высот Z(x) и соответственно третьей степени параметров Pq, Rq, Wg внутри элементарного отрезка:
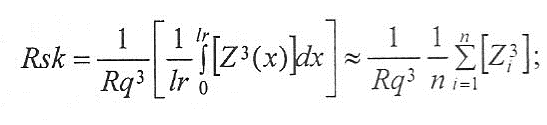
Pku, Rku, WSm - коэффициент эксцесса профиля {kurtosis of the assessed profile) - произведение четвертой степени средних значений высот Z(x) и соответственно четвертой степени параметров Pq,Rq,Wg внутри элементарного отрезка:
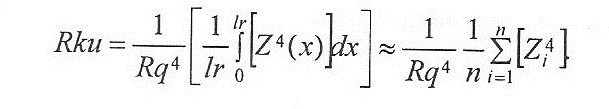
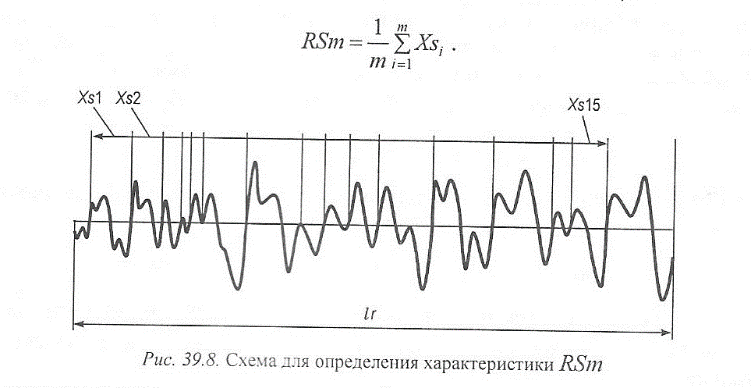
PSw, RSm, WSm - средняя ширина элементов профиля (mean width of the profile elements) элементов профиля Xs находящихся внутри элементарного отрезка (рис. 39.8):
При проведении экспериментов определяли формирование следующих характеристик шероховатости поверхности в зависимости от параметров режима иглофрезерования: среднего арифметического отклонения профиля Ra, стандартного отклонения профиля Rq, высоту десяти точек отклонений от регулярного профиля Rz. общую высоту профиля Rt, максимальную высоту выступов профиля Rp, максимальную глубину впадин профиля Rv, среднюю высоту элементов профиля Rc, среднюю ширину элементов профиля RSm, относительную опорную длину профиля Rmr(c) (рис. 39.9; 39.10):
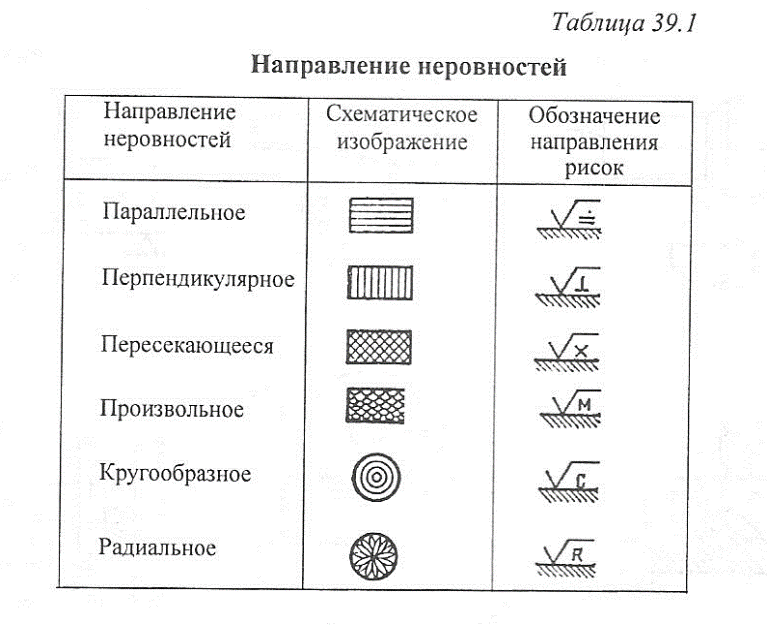
В соответствии с ГОСТ 2789-73 различают 6 направлений неровностей, изображенных в табл. 39.1. Требования к шероховатости конкретной продукции устанавливают на основании знания связи параметров шероховатости с функциональными показателями данного изделия. К настоящему времени накоплен значительный теоретический и экспериментальный материал по связи параметров шероховатости с важнейшими функциональными показателями деталей, узлов машин и приборов, такими, как износостойкость при всех видах трения, контактная жесткость поверхности, износостойкость при переменных нагрузках, прочность прессовых соединений, отражательная способность и затухание в волноводах, прочность сцепления при склеивании, коррозионная стойкость и качество лакокрасочных покрытий, точность измерения, соотношение между допусками размера и шероховатостью поверхности и т. д.
Этот материал может служить основанием для правильного формулирования требований к шероховатости поверхности.
В табл. 38.2 приведены некоторые важнейшие эксплуатационные свойства поверхности, зависящие от шероховатости, и номенклатура параметров, при помощи которых обеспечиваются показатели этого свойства поверхности.
Из данных, приведенных в табл. 39.2, следует, что для полного описания какого-либо эксплуатационного свойства поверхности недостаточно только высотных параметров. Так, износостойкость поверхности при трении скольжения и качения, контактная жесткость и герметичность соединений зависят от опорной поверхности. Такие эксплуатационные характеристики поверхности, как прочность при циклических нагрузках, виброустойчивость, сопротивление (затухание) в волноводах, связаны с амплитудой неровностей (высотными параметрами) и существенно зависят от шаговых параметров Sm и S.

40. КИНЕМАТИКА ПРОЦЕССА РЕЗАНИЯ
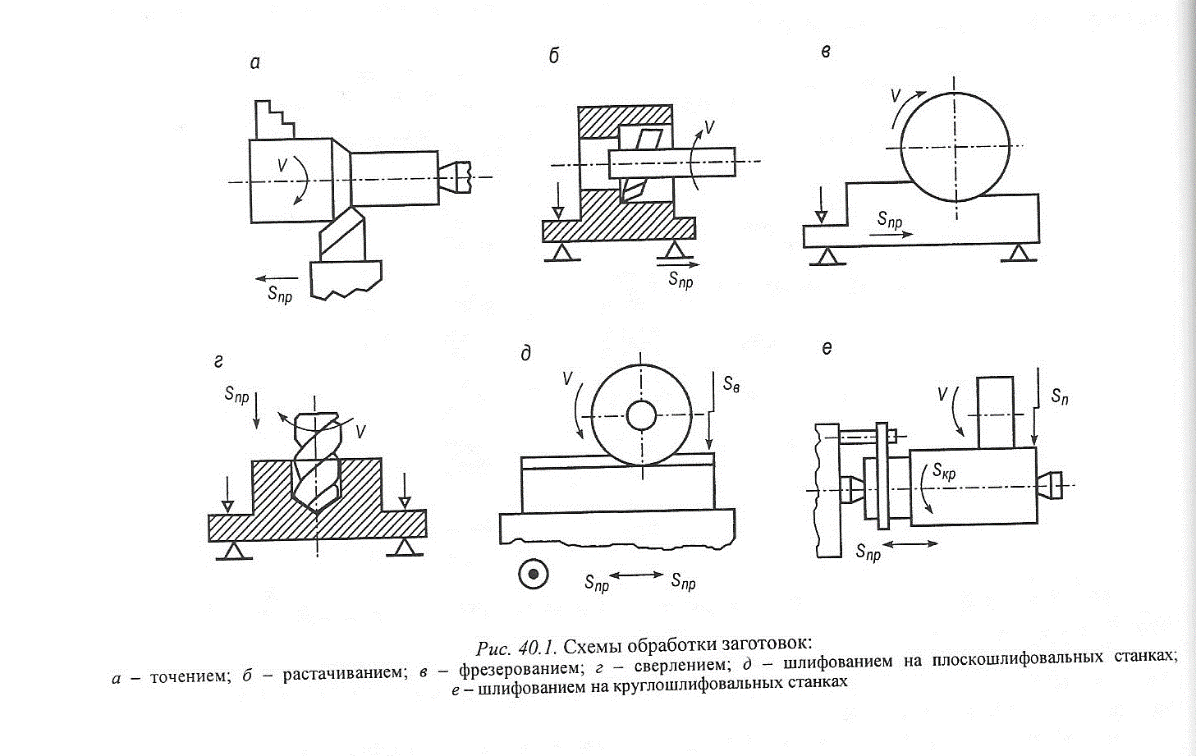
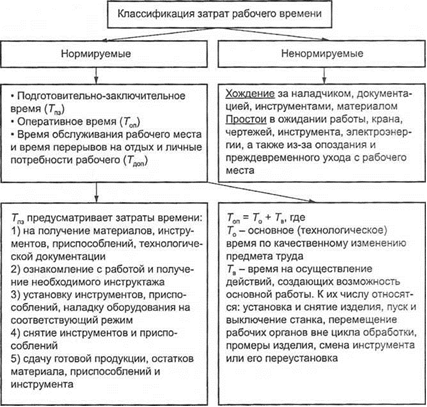
41. КЛАССИФИКАЦИЯ ЗАТРАТ РАБОЧЕГО ВРЕМЕНИ
При всех станочных работах Т0 - основное (технологическое) время - определяется отношением величины пути, пройденного обрабатывающим инструментом, к его минутной подаче (рис. 41.1).
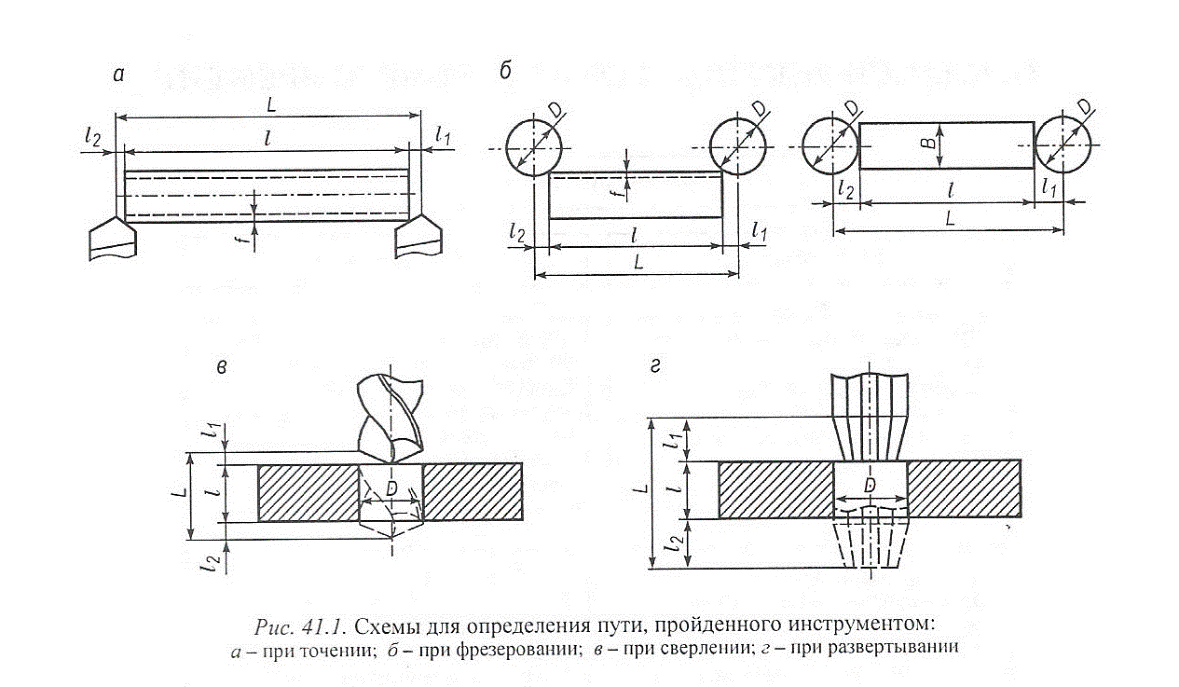
Длина перемещения режущего инструмента
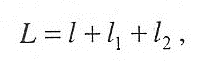
где l - длина обрабатываемой поверхности, мм; l1 - величина врезания инструмента, мм; l2- величина перебега (схода) инструмента, мм.
Основное время Т0 (машинное время Tм) определяется по формуле
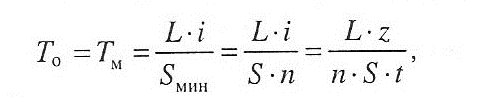
где L- длина перемещения режущего инструмента, мм; Sмин - минутная подача, мм/мин; S - подача на один оборот шпинделя, мм/об; t - глубина резания на сторону, мм; z - припуск на сторону, мм; i - число ходов.
42.ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ПОГРЕШНОСТИ ОБРАБОТКИ
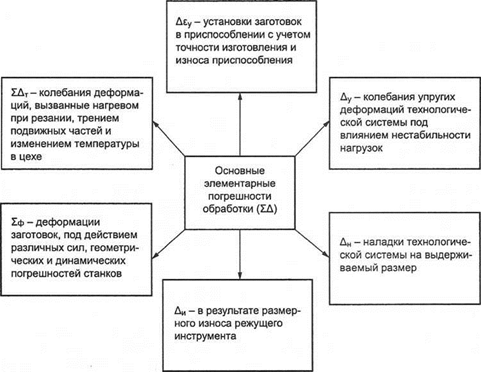
1. Δεy вычисляют с учетом погрешностей: Δεб - базирования; Δεз -закрепления заготовок; Δεпр - изготовления и износа опорных элементов приспособлений. С учетом того, что указанные выше погрешности являются случайными,
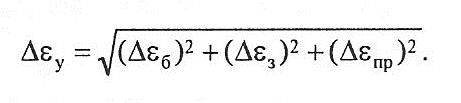
2. Упругие свойства сложных элементов технологических систем, состоящих из нескольких деталей, невозможно определить одним коэффициентом жесткости.
Различают жесткости в направлении осей x,y,z и крутильную жесткость:
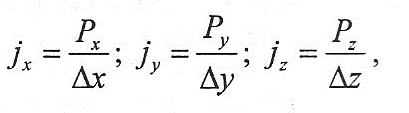
с приращениями сил по х, у, z, соотносящимися с приращениями деформаций по х, у, z;
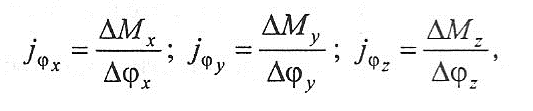
здесь представлено отношение приращений крутящего момента Мх, Му, М: к приращению углов поворота вокруг осей х, у, z .
3. Наладка включает согласованную установку режущего инструмента, рабочих органов станка, режимов, приспособления и т. д., обеспечивающих получение заданного размера. Эти элементы наладки часто называют настройкой (регулированием) технологической системы.
В общем случае Δн зависит от погрешности регулирования Δр положения инструмента (по лимбу, жесткому упору и т.п.) и погрешности измерения детали Δизм . Для плоских поверхностей
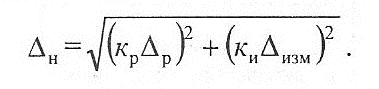
Для поверхностей вращения
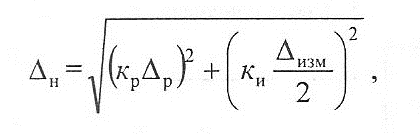
с учетом того Δн и Δр относятся к радиусу, Δизм— к диаметру.
Коэффициенты кр учитывают отклонение закона распределения элементарных величин Δр и Δизм от нормального закона распределения.
4. Размерный износ инструмента Δн измеряют в направлении нормали к обрабатываемой поверхности. За характеристику размерного износа принят относительный (удельный) износ на 1000 м пути резания (u0 мкм/км). Такие виды, как износ по задней поверхности, лункообразование по передней поверхности и т. п., определяются режимами резания, выбором более прочной марки сплава и геометрией.
5. Σф— погрешности формы, вызываемые геометрическими неточностями станка, настройкой станка (овальность, конусообразность, огранка и др.). Погрешность формы Σф относят к систематическим погрешностям.
6. Колебания теплоты в процессе резания (T) образуются в результате внутреннего трения между частицами обрабатываемого материала (Tдеф), внешнего трения стружки о переднюю поверхность инструмента (Тп.тр), заднюю поверхность (Тз.тр), отрыва стружки (диспергирования) (Тдисп):
Т = Тдеф + Тп.тр + Тт.тр + Тдисп .
Полную погрешность обработки ΣΔm обычно определить не удается. Для операций с жесткими допусками ΣΔm = (0,1-0,4) ΔΣ . Для неизвестной обработки ΣΔm = (0,1-0,15) ΔΣ.
Задачу о суммировании решают для каждого случая обработки:
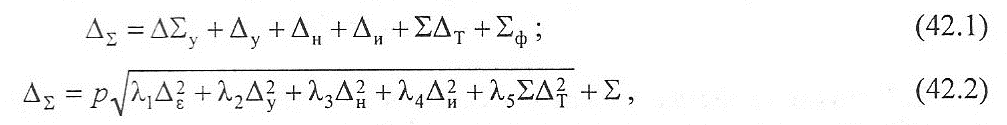
где p - коэффициент, определяющий процент риска получения брака; λ1- λ5 коэффициенты, определяющие законы распределения каждой из элементарных погрешностей.
Расчеты по формуле (42.1) дают завышенный результат. Расчеты по формуле (42.2) выполняют при вероятностной природе элементарных погрешностей. Риск возникает в связи с невозможностью утверждать с полной определенностью, что рассеяние данной элементарной погрешности соответствует данному закону распределения. При р = 1 вероятность данного брака составляет 32 %, при р = 2 она снижается до 4,5 %, при р = 3 снижается до 0,27 %. Из практики известно, что λ1 = λ2 = λ3 =1/9, поскольку соответствующие погрешности подчиняются закону Гаусса; λ4 = 1/3 – распределение соответствует закону равной вероятности; λ5 = 1/3 – закон распределения ΣΔm малоизвестен . При р=3
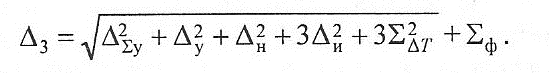
43. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Для практической оценки дифференциальной функции распределения плотностей вероятности разделяют на три группы: точечные, интервальные и характеристики, связанные со всей областью существования функции.
Точечные характеристики отражают значение функции плотностей вероятностей относительно некоторых точек на оси х. К ним относятся: мода, медиана и интенсивность.
Мода - такое значение х (случайной величины), которому соответствует максимум функции плотности. Если f(x1)= mах, то x1=M0(x). Если функция f(x) имеет два максимума, то такой закон называют 2-модальным, три максимума - 3-модальным.
Медиана - Ме(х) = х1, если Р {х < x1} = Р {х > x1} = 0,5.
Если число деталей четное, то медианой считают среднее арифметическое между двумя средними числами.
Пример. Пусть в выборке 6 размеров, мм: 14,90; 14,92; 14,93; 14.95; 14,97; 14,98, расположенных по степени возрастания, тогда
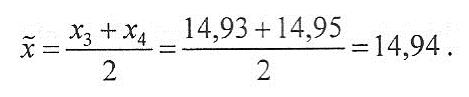
Пример. Пусть в выборке 5 деталей с размерами: 14,93; 14,92; 14,97; 14,92; 14,98. Расположим ряд по степени возрастания: 14,92; 14,92; 14,93; 14,97; 14,98, тогда 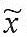 = х3 = 14,93 .
= х3 = 14,93 .
Интенсивность:
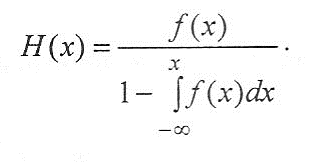
К интервальным относятся следующие характеристики.
1. Вероятность попадания случайной величины в некоторый фиксированный интервал значений Δх = (хi, хi+1) :
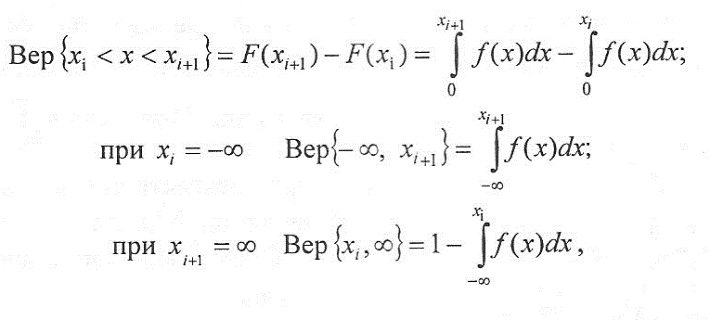
так как 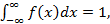
2. Границы поля рассеяния можно выразить квантилями. Интервальная оценка определяется концами интервала. К характеристикам, охватывающим всю область существования функции, относятся начальный и центральный моменты n-го порядка.
Начальный момент n-го порядка: φ(х) = 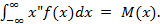
Начальный момент 1-го порядка (математическое ожидание) характеризует положение случайной величины на осях: φ1(x) = М(х) = 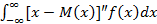
Центральный момент п-го порядка: Ψ(x) = 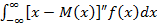
Второй центральный момент: Ψ(x) = D(x) = 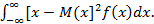
D(x) характеризует степень рассеяния случайной величины. Для характеристики рассеяния пользуются средним квадратическим отклонением:
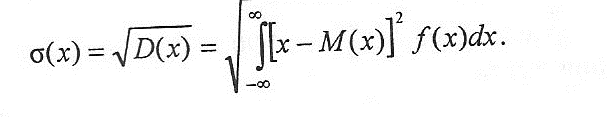
Например, пусть дифференциальная функция нормального распределения задана кривой Гаусса:
y = f(x) = 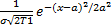 .
.
Здесь М(х) = a; 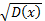 = σ.
= σ.
Если z = 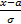 – нормативная нормальная величина, причем M(z) = 0; σ = 1, то
– нормативная нормальная величина, причем M(z) = 0; σ = 1, то
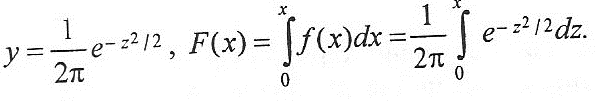
Кривые f(x — a)u f (х) отличаются смещением без изменения формы в положительном направлении оси х на величину а, т.е. изменение М(х) не изменяет формы кривой Гаусса. Если а > 0, то кривая смещается в положительном направлении оси х; если а < 0 - в обратном направлении
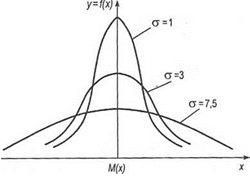
Рис. 43.1. Влияние значений среднеквадратиче-
ских рассеяния случайной величины σ на
изменения формы кривой рассеяния
При x = a 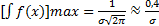 , т.е. при возрастании а максимальное значение функции убывает, а сама кривая становится более пологой (сжимается к оси х) (рис. 43.1).
, т.е. при возрастании а максимальное значение функции убывает, а сама кривая становится более пологой (сжимается к оси х) (рис. 43.1).
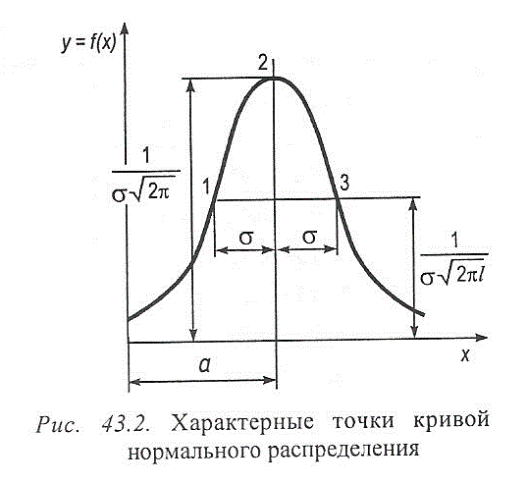
Характерные точки кривой нормального распределения (рис. 43.2):
1 – { a-σ ; 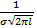 };
};
2 – { a+σ; 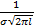 };
};
3 – { a; 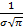 }.
}.
При а = а, δ = 1 у = f(x) имеет нормированный вид.
При любых значениях а и δ 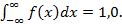
Для эмпирического (дискретного) рассеяния характеристика положения центра рассеяния приводится в виде средней арифметической, взвешенной по частям значений величины.
Кривая асимптотически приближается к оси абсцисс. На расстоянии ±3σ За от положения вершины кривой оказывается 99,73 % площади, заключенной между всей кривой нормального распределения, поэтому составляющая 0,27 % практического значения не имеет.
Фактическое поле рассеяния размеров заготовок  = 6σ. Под влиянием систематической и случайной погрешностей вершина кривой распределения может смещаться по отношению к середине поля рассеяния в ту или иную сторону, а форма кривой может изменяться.
= 6σ. Под влиянием систематической и случайной погрешностей вершина кривой распределения может смещаться по отношению к середине поля рассеяния в ту или иную сторону, а форма кривой может изменяться.
Закон нормального распределения (закон Гаусса) в большинстве случаев оказывается справедлив при механической обработке заготовок с точностью 8, 9, 10 (и грубее) квалитетов.
44. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Математическая статистика оперирует эмпирическими (статистическими, экспериментальными) значениями случайных величин. При этом достаточно знать следующее.
1.Примерное расположение узкого интервала значений величины, в котором находится основная масса вероятностей (частостей), т.е. среднее значение величины, вокруг которого группируются (достаточно тесно) эти значения.
2.Как и на сколько рассеяна масса вероятностей (частость) около центра группирования. Например, после измерения n = 100 штук заготовок с действительными размерами в пределах от 20,00 до 20,35 мм распределение размеров представлено табличными значениями (рис. 44.1, табл. 44).
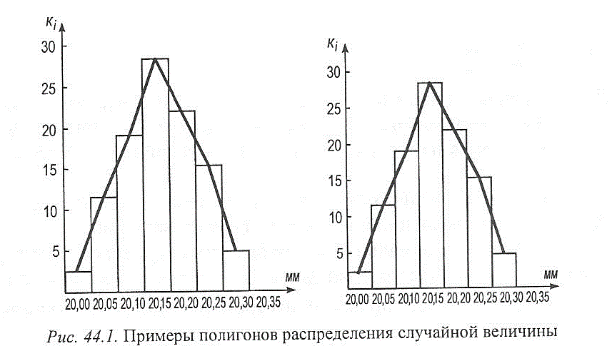
Таблица 44
| Интервал, мм | Частота ki | Частота W = 
|
| 20,00-20,05 | 0,02 | |
| 20,05-20,10 | 0,11 | |
| 20,10-20,15 | 0,19 | |
| 20,15-20,20 | 0,28 | |
| 20,20-20,25 | 0,22 | |
| 20,25-20,30 | 0,15 | |
| 20,30-20,35 | 0,03 | |
| Итого | п = 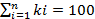
| W = 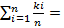 1 1
|
Справа и слева зависимость соответствующей частоты п = 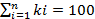 и частотей
и частотей
W = 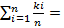 1, называемая гистограммой распределения. Если последовательно соединить между собой точки, соответствующие середине каждого интервала, то образуется ломаная кривая, которая носит название эмпирической кривой распределения или полигона распределения. Для построения гистограммного распределения рекомендуется результаты измерения разбивать не менее чем на 6 интервалов при общем числе измеренных заготовок не меньше 50 шт. При этом ломаная эмпирическая кривая приближается по форме к плавной кривой, именуемой кривой распределения. W =
1, называемая гистограммой распределения. Если последовательно соединить между собой точки, соответствующие середине каждого интервала, то образуется ломаная кривая, которая носит название эмпирической кривой распределения или полигона распределения. Для построения гистограммного распределения рекомендуется результаты измерения разбивать не менее чем на 6 интервалов при общем числе измеренных заготовок не меньше 50 шт. При этом ломаная эмпирическая кривая приближается по форме к плавной кривой, именуемой кривой распределения. W = 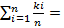 Fэмп (x) стремится к вероятности Fтеор (x) этого события.
Fэмп (x) стремится к вероятности Fтеор (x) этого события.
За центр группирования принимается «центр тяжести» этих масс (сравните связь с геометрией масс в механике):
 c =
c = 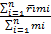 ,
,
т.е а = xср = 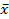 с = M (x) =
с = M (x) = 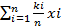
Из последнего уравнения видно, что при дискретном (эмпирическом) распределении случайной величины математическое ожидание есть абсцисса центра масс системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы - их вероятностям (частостям).
Для эмпирического распределения характеристика положения центра рассеяния приводится в виде средней арифметической взвешенной по частям значений величины 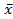 .
.
Как отмечалось выше, при нормальном и других симметричных, одновершинных законах распределения М(х), 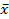 медиана и мода совпадают. На практике это происходит при отсутствии систематических погрешностей (при проверке настройки станка на среднюю точку поля допуска).
медиана и мода совпадают. На практике это происходит при отсутствии систематических погрешностей (при проверке настройки станка на среднюю точку поля допуска).
45. НЕКОТОРЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
Закон Симпсона
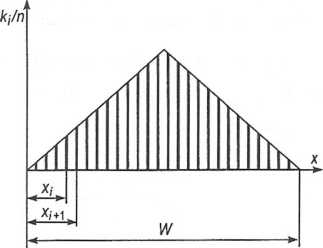 Рис. 45.1. Графическое изображение закона Симпсона
Рис. 45.1. Графическое изображение закона Симпсона
|
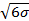 ≈ 4,9σ. Среднее квадратическое отклонение
≈ 4,9σ. Среднее квадратическое отклонение
σ = 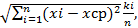
где xi- частота (количество заготовок, попадающих в интервал Δх размеров); xср = 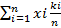 - среднее взвешенное арифметическое значение действительных размеров в партии.
- среднее взвешенное арифметическое значение действительных размеров в партии.
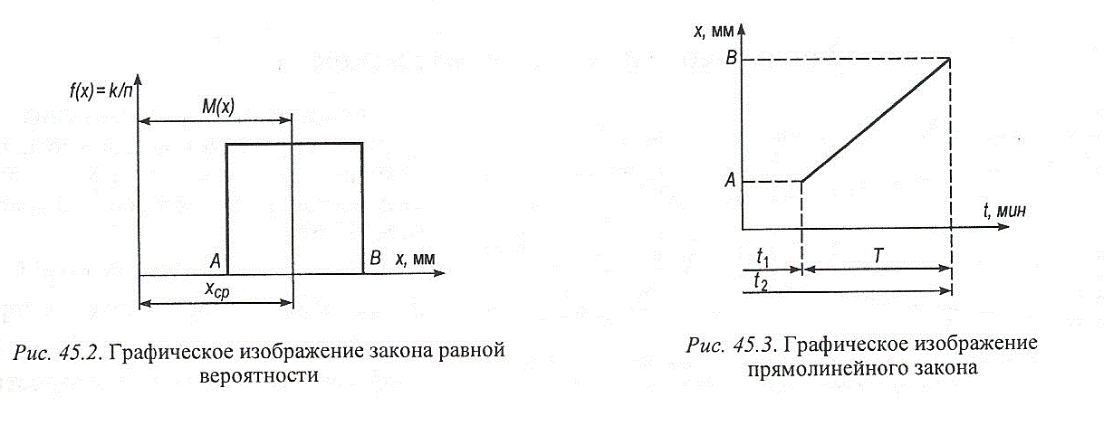
Закон равной вероятности
Если рассеивание размеров зависит от переменных систематических погрешностей (например, от износа инструмента), то распределение их подчиняется закону равной вероятности.
При установившемся износе режущего инструмента распределение размеров вала увеличивается, а отверстия - уменьшается. Если непрерывная случайная величина х принимает все значения интервала А - В с одинаковой плотностью вероятности, то это распределение графически будет выражаться в виде прямоугольника с основанием АВ и высотой f(х) = const (рис. 45.2). Распределение размеров при равномерном износе во времени подчиняется прямолинейному закону (рис. 45.3).
M (x) = 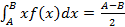 ;
;
σ2 = 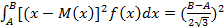 .
.
Площадь прямоугольника равна единице. Это означает 100 %-ную вероятность появления размера в интервале от А до В, 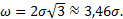
Закон эксцентриситета (закон Рэлея)
Отражает распределение величин, характеризующихся их абсолютными значениями (т. е. без учета знака). К этим величинам относятся: эксцентриситет, биение, разностенность, отклонение от параллельности, отклонение от перпендикулярности.
Например, описывая формирование эксцентриситета  втулки при двухмерном гауссовском распределении двух случайных величин х и у с параметрами хср = уср = rср = 0 ;
втулки при двухмерном гауссовском распределении двух случайных величин х и у с параметрами хср = уср = rср = 0 ; 
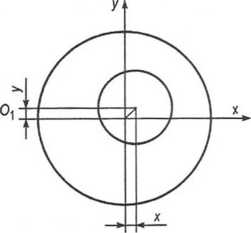
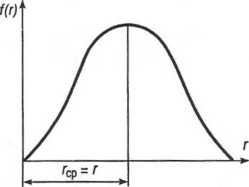
Рис. 45.4. Схема для определения параметров эксцентриситета
Рис. 45.5. Графическое изображение закона Рэлея
Закон распределения Рэлея однопараметрический (рис. 45.4):
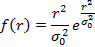
Интегральный закон распределения эксцентриситета имеет следующий вид (рис. 45.5):
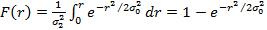 ;
;
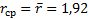 ;
; 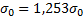 ;
; 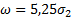 ;
; 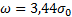 .
.
Дата добавления: 2017-06-02; просмотров: 2245;
