Емпірична функція розподілу
Як відомо, закон розподілу будь-якої випадкової величини 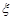 можна задавати функцією розподілу
можна задавати функцією розподілу 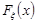 . Якщо мати вибірку значень цієї випадкової величини, то можна побудувати деяке наближення функції розподілу.
. Якщо мати вибірку значень цієї випадкової величини, то можна побудувати деяке наближення функції розподілу.
Означення 27.10. Емпіричною функцією розподілу називається функція розподілу дискретної випадкової величини, що набуває значення варіант 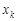 з ймовірністю
з ймовірністю 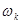 , тобто:
, тобто:
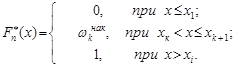 (27.3)
(27.3)
де 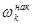 =
= 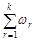 , тобто накопичена частість.
, тобто накопичена частість.
Очевидно, що 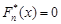 при
при 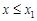 і
і 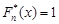 при
при 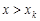 . На проміжку
. На проміжку 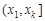
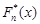 є неспадною кусково-сталою функцією.
є неспадною кусково-сталою функцією.
Аналогічно визначається емпірична функція розподілу для інтервального варіаційного ряду. Оскільки, ми маємо лише значення емпіричної функції 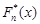 на кінцях інтервалів, то для графічного її зображення доцільно до визначити
на кінцях інтервалів, то для графічного її зображення доцільно до визначити 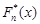 , з’єднав точки графіка, які відповідають кінцям інтервалів, відрізками прямої. В результаті отримана ламана співпаде з кумулятою.
, з’єднав точки графіка, які відповідають кінцям інтервалів, відрізками прямої. В результаті отримана ламана співпаде з кумулятою.
Приклад 27.7. Побудувати емпіричну функцію розподілу вибірки, що представлена інтервальним варіаційним рядом прикладу 27.5.
Розв’язання. Для побудови графіка емпіричної функції розподілу використаємо формулу (27.3) та значення табл. 27.3.
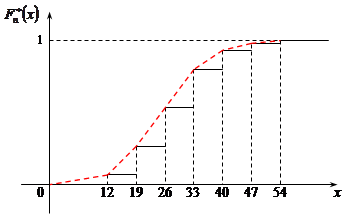 |
Рис.27.3.
Із теореми Бернуллі випливає, що емпірична функція розподілу 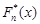 при
при 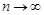 прямує за ймовірністю до функції розподілу
прямує за ймовірністю до функції розподілу 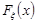 . Крім того, візьмемо до уваги теорему Глівенко - Кантеллі, згідно якої,
. Крім того, візьмемо до уваги теорему Глівенко - Кантеллі, згідно якої, 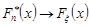 при
при 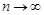 із ймовірністю 1 рівномірно відносно х.
із ймовірністю 1 рівномірно відносно х.
Дата добавления: 2017-05-18; просмотров: 2860;
