Оцінювання параметрів розподілу випадкової величини
Нехай 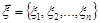 – вибірка з генеральної сукупності з законом розподілу
– вибірка з генеральної сукупності з законом розподілу 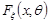 . Причому функція розподілу спостережуваної випадкової величини
. Причому функція розподілу спостережуваної випадкової величини 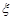 має відому функціональну форму, але залежить від невідомого параметра
має відому функціональну форму, але залежить від невідомого параметра 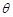 . Наприклад, це параметр
. Наприклад, це параметр 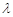 в показниковому законі або параметри
в показниковому законі або параметри 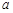 та
та 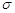 в законі Гаусса тощо. Для знаходження параметра
в законі Гаусса тощо. Для знаходження параметра 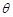 дослідити всі елементи генеральної сукупності неможливо, тому для оцінювання параметра
дослідити всі елементи генеральної сукупності неможливо, тому для оцінювання параметра 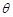 використовують вибірку та реалізації вибірки
використовують вибірку та реалізації вибірки 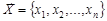 . Надалі множину значень параметра
. Надалі множину значень параметра 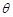 назвемо параметричною множиною
назвемо параметричною множиною 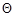 .
.
Означення 29.1. Точковою оцінкою 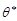 параметра
параметра 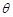 називають будь-яку функцію результатів спостережень над випадковою величиною
називають будь-яку функцію результатів спостережень над випадковою величиною 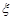 (статистику), за допомогою якої судять про значення параметру
(статистику), за допомогою якої судять про значення параметру 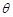 :
:
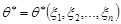 .
.
Зрозуміло, що точкова оцінка 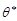 , на відміну від параметра
, на відміну від параметра 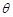 , є випадковою величиною, яка залежить від закону розподілу випадкової величини
, є випадковою величиною, яка залежить від закону розподілу випадкової величини 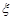 та обсягу вибірки. Безумовно можна ввести багато функцій від результатів спостережень, які можна брати в якості параметра
та обсягу вибірки. Безумовно можна ввести багато функцій від результатів спостережень, які можна брати в якості параметра 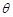 . Наприклад, якщо параметр
. Наприклад, якщо параметр 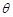 є математичним сподіванням випадкової величини
є математичним сподіванням випадкової величини 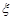 , то за оцінку математичного сподівання за результатами спостережень можна взяти: середнє арифметичне
, то за оцінку математичного сподівання за результатами спостережень можна взяти: середнє арифметичне 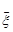 , моду
, моду 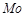 , медіану
, медіану 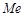 , півсуму найбільшого та найменшого значення за вибіркою тощо. Отже, яку статистику краще вибрати? Назвати “найкращою” оцінку ту, яка найбільш близька до істинного значення оцінюваного параметру неможливо, оскільки точкова оцінка
, півсуму найбільшого та найменшого значення за вибіркою тощо. Отже, яку статистику краще вибрати? Назвати “найкращою” оцінку ту, яка найбільш близька до істинного значення оцінюваного параметру неможливо, оскільки точкова оцінка 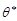 – випадкова величина, то не можна передбачити значення оцінки в кожному конкретному випадку. Таким чином, про якість оцінки можна судити не по її конкретним значенням, а лише по вибірковому розподілу оцінки. В зв’язку з цим розглянемо вимоги, що висувають до оцінок.
– випадкова величина, то не можна передбачити значення оцінки в кожному конкретному випадку. Таким чином, про якість оцінки можна судити не по її конкретним значенням, а лише по вибірковому розподілу оцінки. В зв’язку з цим розглянемо вимоги, що висувають до оцінок.
29.2. Незміщені точкові оцінки параметрів розподілів
Означення 29.2. Точкова оцінка 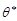 параметра
параметра 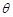 називається незміщеною, якщо її математичне сподівання дорівнює оцінюваному параметру
називається незміщеною, якщо її математичне сподівання дорівнює оцінюваному параметру 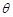 , тобто
, тобто
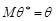 або
або 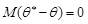 . (29.1)
. (29.1)
Якщо умова (29.1) не виконується, то оцінка 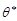 , яка отримана за різними вибірками, буде в середньому або завищувати значення параметру
, яка отримана за різними вибірками, буде в середньому або завищувати значення параметру 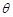
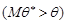 , або це значення знижувати
, або це значення знижувати 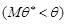 . Отже, вимога (29.1) гарантує відсутність систематичних помилок. Якщо
. Отже, вимога (29.1) гарантує відсутність систематичних помилок. Якщо 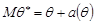 , то величину
, то величину 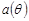 називають зсувом точкової оцінки.
називають зсувом точкової оцінки.
Приклад 29.1. Перевірити незміщеність вибіркового середнього 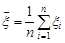 , як точкової оцінки математичного сподівання випадкової величини
, як точкової оцінки математичного сподівання випадкової величини 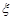 .
.
Розв’язання. Перевіримо виконання умови (29.1) для вибіркового середнього:
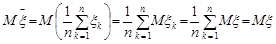 .
.
Отже, незалежно від закону розподілу генеральної сукупності випадкової величини 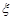 оцінка
оцінка 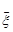 буде завжди незміщеною для математичного сподівання.
буде завжди незміщеною для математичного сподівання.
Приклад 29.2. Нехай відомо математичне сподівання випадкової величини 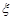 . Перевірити незміщеність вибіркової дисперсії
. Перевірити незміщеність вибіркової дисперсії 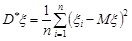 , як точкової оцінки дисперсії випадкової величини
, як точкової оцінки дисперсії випадкової величини 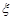 .
.
Розв’язання. Перевіримо виконання умови (29.1) для вибіркової дисперсії:
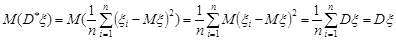 .
.
Отже, незалежно від закону розподілу генеральної сукупності випадкової величини 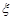 оцінка
оцінка 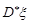 буде завжди незміщеною для дисперсії при умові, що математичне сподівання
буде завжди незміщеною для дисперсії при умові, що математичне сподівання 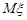 відомо.
відомо.
Приклад 29.3. Нехай математичне сподівання випадкової величини 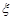 невідомо. Перевірити незміщеність вибіркової дисперсії
невідомо. Перевірити незміщеність вибіркової дисперсії 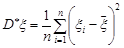 , як точкової оцінки дисперсії випадкової величини
, як точкової оцінки дисперсії випадкової величини 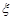 .
.
Розв’язання. За формулою (28.2) вибіркову дисперсію можна записати у вигляді 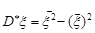 . Покажемо, що величина вибіркової дисперсії не зміниться, якщо цю формулу записати у вигляді
. Покажемо, що величина вибіркової дисперсії не зміниться, якщо цю формулу записати у вигляді
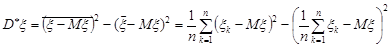 .(29.2)
.(29.2)
Дійсно
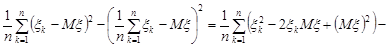
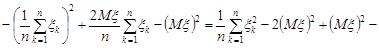
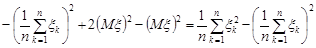 .
.
Знайдемо математичні сподівання кожного з доданків виразу (29.2). Із результатів прикладу 29.2
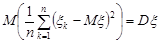 .
.
Математичне сподівання другого доданку формули (29.2) дорівнює
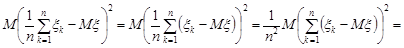
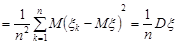 .
.
Остаточно
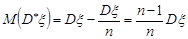 .
.
Отже, вибіркова дисперсія у випадку невідомого математичного сподівання випадкової величини 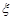 буде зміщеною точковою оцінкою. Для того, щоб ліквідувати зсув, вводять виправлену вибіркову дисперсію
буде зміщеною точковою оцінкою. Для того, щоб ліквідувати зсув, вводять виправлену вибіркову дисперсію
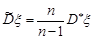 .
.
Виправлена вибіркова дисперсія буде незміщеною точковою оцінкою дисперсії у випадку невідомого математичного сподівання. Дійсно
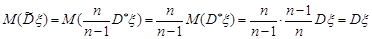 .
.
Зауважимо, якщо обсяг вибірки достатньо великий (при 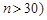 , вибіркова дисперсія та виправлена вибіркова дисперсія майже не відрізняються.
, вибіркова дисперсія та виправлена вибіркова дисперсія майже не відрізняються.
Приклад 29.4. Нехай є вибірка 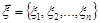 з рівномірного розподілу на проміжку
з рівномірного розподілу на проміжку 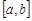 . Розглянемо статистику
. Розглянемо статистику 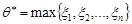 . Чи можна точкову оцінку
. Чи можна точкову оцінку 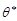 розглядати як незміщену точкову оцінку або параметра
розглядати як незміщену точкову оцінку або параметра 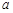 , або параметра
, або параметра 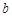 рівномірного закону?
рівномірного закону?
Розв’язання. Знайдемо закон розподілу точкової оцінки 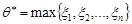 . Функція розподілу оцінки
. Функція розподілу оцінки 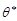 дорівнює
дорівнює
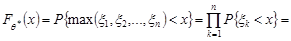
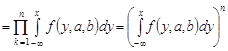 .
.
Звідси отримаємо щільність розподілу точкової оцінки 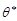 :
:
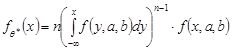 =
=
= 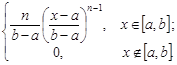
Знайдемо математичне сподівання точкової оцінки 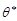 .
.
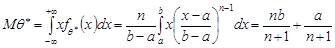 .
.
Отже, оцінка 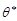 не є незміщеною оцінкою ні параметра
не є незміщеною оцінкою ні параметра 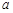 , ні параметра
, ні параметра 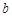 . Проте зауважимо, що
. Проте зауважимо, що
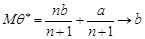 при
при 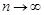 .
.
Це означає, що оцінка 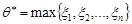 є асимптотично незміщеною оцінкою параметра
є асимптотично незміщеною оцінкою параметра 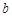 .
.
Аналогічно можна довести, що для оцінки 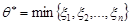 математичне сподівання дорівнює
математичне сподівання дорівнює
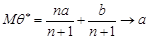 при
при 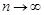 .
.
29.3. Конзистентні (спроможні) оцінки параметрів розподілу
Розглянемо залежність точкової оцінки 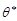 параметра розподілу
параметра розподілу 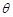 від обсягу вибірки
від обсягу вибірки 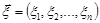 , тобто будемо розглядати цілу послідовність оцінок
, тобто будемо розглядати цілу послідовність оцінок 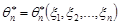 .
.
Означення 29.3. Послідовність точкових оцінок 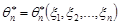 ,
, 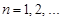 параметра розподілу
параметра розподілу 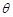 називається конзистентною (спроможною), якщо задовольняє закону великих чисел, тобто збігається за ймовірністю до параметра
називається конзистентною (спроможною), якщо задовольняє закону великих чисел, тобто збігається за ймовірністю до параметра 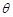 при
при 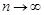 :
:
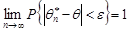 . (29.3)
. (29.3)
У випадку використання конзистентних оцінок виправдано використання вибірок великого обсягу, тому що при цьому стають малоймовірними значні помилки при оцінюванні. Отже, практичний зміст мають лише конзистентні оцінки.
Приклад 29.5. Перевірити конзистентність оцінки 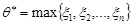 приклада 29.4.
приклада 29.4.
Розв’язання. Перевіримо, чи буде точкова оцінка 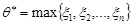 збігатися за ймовірністю до параметра
збігатися за ймовірністю до параметра 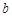 при
при 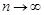 . Маємо
. Маємо
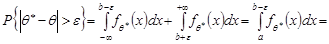
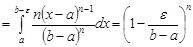 .
.
Останній вираз прямує до 0 при 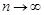 . Це означає, що оцінка
. Це означає, що оцінка 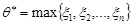 є конзистентною.
є конзистентною.
Наведемо достатньо простий критерій конзистентності незміщених оцінок.
Нехай точкова оцінка 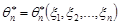 є незміщеною оцінкою параметра
є незміщеною оцінкою параметра 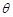 , тобто виконується умова (29.1), тоді за нерівністю Чебишева маємо
, тобто виконується умова (29.1), тоді за нерівністю Чебишева маємо
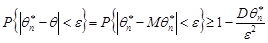 .
.
З цієї нерівності випливає, що, якщо
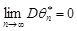 ,
,
то незміщена точкова оцінка буде конзистентною.
Приклад 29.6. Перевірити конзистентність вибіркового середнього 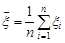 випадкової величини
випадкової величини 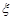 .
.
Розв’язання. Оскільки 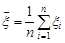 є незміщеною оцінкою математичного сподівання випадкової величини
є незміщеною оцінкою математичного сподівання випадкової величини 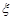 , то згідно наведеного критерію, знайдемо дисперсію вибіркового середнього.
, то згідно наведеного критерію, знайдемо дисперсію вибіркового середнього.
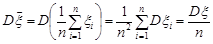 .
.
Отже, 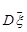 прямує до 0 при
прямує до 0 при 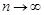 , що означає конзистентність вибіркового середнього.
, що означає конзистентність вибіркового середнього.
Приклад 29.7. Перевірити конзистентність вибіркової дисперсії 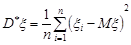 у випадку відомого математичного сподівання
у випадку відомого математичного сподівання 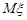 .
.
Розв’язання. Як випливає з прикладу 29.2, вибіркова дисперсія 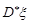 , у випадку відомого математичного сподівання
, у випадку відомого математичного сподівання 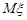 , є незміщеною оцінкою математичного сподівання. Знайдемо її дисперсію:
, є незміщеною оцінкою математичного сподівання. Знайдемо її дисперсію:
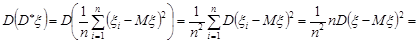
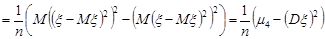 .
.
Отже, якщо випадкова величина 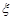 має скінчений четвертий центральний момент, то вибіркова дисперсія є конзистентною оцінкою дисперсії випадкової величини.
має скінчений четвертий центральний момент, то вибіркова дисперсія є конзистентною оцінкою дисперсії випадкової величини.
Якщо математичне сподівання випадкової величини 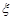 невідомо, то з прикладу 29.3 випливає, що незміщеною оцінкою дисперсії буде виправлена вибіркова дисперсія
невідомо, то з прикладу 29.3 випливає, що незміщеною оцінкою дисперсії буде виправлена вибіркова дисперсія 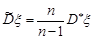 . Конзистентність цієї оцінки випливає з того, що
. Конзистентність цієї оцінки випливає з того, що
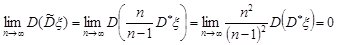 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Закони розподілів емпіричних характеристик генеральної сукупності | | | Довірчий інтервал для математичного сподівання нормального розподілу |
Дата добавления: 2017-05-18; просмотров: 1961;
