Закони розподілів емпіричних характеристик генеральної сукупності

Оскільки будь-яка статистика вибіркового вектора 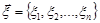є випадковою величиною, то вона має свій закон розподілу, який не завжди легко отримати в явному вигляді.

В окремих випадках, застосовуючи центральну граничну теорему можна знайти асимптотичні закони розподілу статистик. Наприклад, для емпіричних моментів 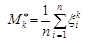генеральної сукупності можна стверджувати, що послідовність їх функцій розподілу 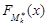збігається в основному при 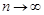рівномірно відносно х до закону Гаусса з параметрами 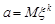та середньоквадратичного відхилення 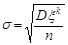. Іншими словами, можна вважати, що статистика 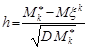розподілена асимптотично нормально з параметрами (0, 1).

В інших випадках, коли статистика 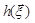задається формулою

,

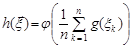де 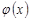, 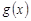– неперервні функції на R¹, також можна довести, що вона має асимптотично нормальний розподіл.

Виникає запитання, при яких n закон розподілу статистики 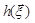можна вважати достатньо близьким до нормального?

Запитання складне й відповісти на нього однозначно не можна. Все залежить як від самої генеральної сукупності, так і від статистики.

В тих випадках коли обсяг вибірки n недостатньо великий, користуватись асимптотичними виразами взагалі не можна й доводиться шукати точні закони розподілу статистики. Існують чотири методи їх знаходження. Перший полягає в знаходженні функції розподілу 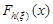статистики 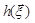, виходячи із означення функції розподілу, тобто

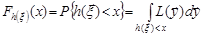. (28.6)

Другий метод – геометричний, при якому іноді вдається так інтерпретувати інтегрування, що це дозволяє уникнути складних обчислень інтегралів типу (28.6).

Третій метод застосовує апарат характеристичних функцій. Використання характеристичних функцій базується на тому, що характеристична функція суми незалежних випадкових величин дорівнює добутку характеристичних функції цих величин. Це дає можливість обчислювати функції розподілу статистик типу 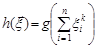. До четвертого методу відносять всі інші аналітичні методи, в тому числі метод математичної індукції. Розглянемо ці методи на деяких прикладах.

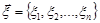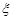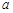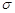Приклад 28.1. Нехай є вибірка з генеральної сукупності , розподіленої за законом Гаусса з параметрами та . Знайти закон розподілу статистики .

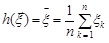Розв’язання. Оскільки закон Гаусса є стійким законом розподілу, то статистика 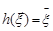розподілена також за нормальним законом. Знайдемо параметри цього закону, враховуючи, що компоненти вибірки є незалежними випадковими величинами.

.

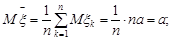
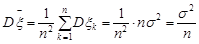Приклад 28.2. Нехай 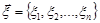є вибірка з генеральної сукупності 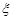, розподіленої за законом Пуассона з параметром 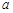. Знайти закон розподілу статистики .

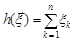Розв’язання. Закон розподілу заданої статистики знайдемо, використовуючи апарат характеристичних функцій. Позначимо за 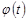характеристичну функцію суми 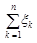. За властивістю характеристичних функцій

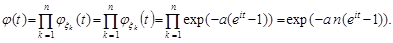
Отримана характеристична функція є характеристичною функцією закону Пуассона з параметром 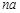. Отже, статистика 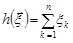розподілена за законом Пуассона з параметром .

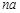Приклад 28.3. 1. Нехай 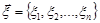є вибірка з генеральної сукупності 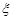, розподіленої за законом Гаусса з параметрами та 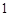. Знайти закон розподілу статистики 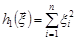. 2. Нехай 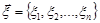є вибіркою генеральної сукупності 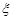, розподіленої за законом Гаусса з параметрами 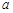та 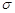. Знайти закон розподілу статистики .

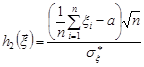Розв’язання. 1. В лекції 23 було доведено, що випадкова величина 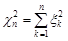розподілена за законом “хі-квадрат з 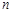ступенями вільності”. Отже, розподілом статистики 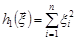буде розподіл “хі-квадрат з 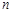ступенями вільності. 2. Розподіл Стьюдента мають випадкової величини 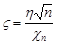, де величина 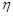має нормальний розподіл 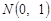, а величина 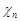має розподіл “хі з 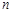ступенями вільності” та обидві вони незалежні. Розглянемо випадкову величину 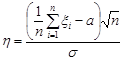. Вона має нормальний розподіл з параметрами 0 та 1. Розподіл 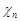з 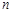ступенями вільності має випадкова величина 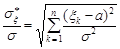. Таким чином, статистика 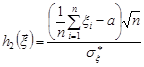має розподіл Стьюдента з 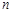ступенями вільності.