Означення емпіричних (вибіркових) характеристик генеральної сукупності
Нехай задано вибірковий вектор 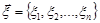 з генеральної сукупності випадкової величини
з генеральної сукупності випадкової величини 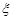 .
.
Означення 28.1. Функція 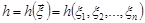 від вибіркового вектора
від вибіркового вектора 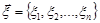 називається статистикою.
називається статистикою.
Якщо статистика  , то вона є випадкова величина.
, то вона є випадкова величина.
Найбільш розповсюджені статистики – це емпіричні (вибіркові) моменти.
Означення 28.2. Вибірковим моментом порядку k називається величина
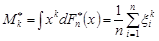 .
.
Вибірковим центральним моментом порядку k називається величина
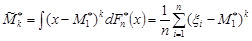 .
.
Вибірковий момент першого порядку найчастіше називають вибірковим (емпіричним) середнім і позначають
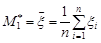 .
.
Реалізацію вибіркового середнього будемо позначати 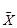 . Якщо
. Якщо 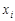 є варіантами дискретного варіаційного ряду,
є варіантами дискретного варіаційного ряду, 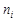 – відповідні їм частоти, то вибіркове середнє обчислюється так:
– відповідні їм частоти, то вибіркове середнє обчислюється так:
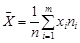 . (28.1)
. (28.1)
У випадку інтервального варіаційного ряду за значення 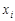 беруть середини інтервалів варіаційного ряду. Очевидно, що в цьому випадку
беруть середини інтервалів варіаційного ряду. Очевидно, що в цьому випадку 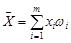 , де
, де 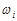 – відповідні частості варіантів або інтервалів.
– відповідні частості варіантів або інтервалів.
Вибірковий центральний момент другого порядку називають вибірковою (емпіричною) дисперсією та позначають
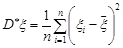 .
.
Зауважимо, що вибіркову дисперсію можна записати так:
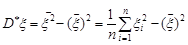 . (28.2)
. (28.2)
Доведення. Дійсно
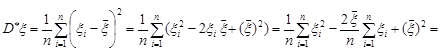
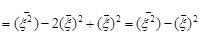 .
.
Реалізацію вибіркової дисперсії позначимо 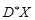 . Якщо
. Якщо 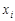 є варіантами дискретного варіаційного ряду,
є варіантами дискретного варіаційного ряду, 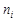 – відповідні їм частоти, то вибіркова дисперсія обчислюється так:
– відповідні їм частоти, то вибіркова дисперсія обчислюється так:
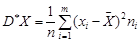 .
.
У випадку інтервального варіаційного ряду за значення 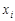 беруть також середини інтервалів варіаційного ряду. Очевидно, що
беруть також середини інтервалів варіаційного ряду. Очевидно, що 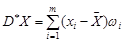 , де
, де 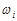 – відповідні частості варіантів або інтервалів.
– відповідні частості варіантів або інтервалів.
Формула (28.2) для реалізації вибіркової дисперсії набуває вигляду
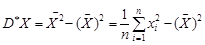 . (28.3)
. (28.3)
Якщо математичне сподівання випадкової величини 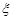 відомо, то природно, що за вибіркову дисперсію беруть величину
відомо, то природно, що за вибіркову дисперсію беруть величину
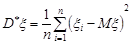 .
.
Крім вибіркової дисперсії розглядають також вибіркове середнє квадратичне або стандартне відхилення 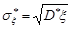 .
.
Розглянуті вище статистики називають аналітичними. У математичній статистиці застосовують також порядкові статистики. До таких статистик належать емпірична мода, емпірична медіана, емпіричний коефіцієнт асиметрії та ексцес.
Емпіричною (вибірковою) модою 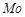 називається варіанта, якій відповідає найбільша частість. Особливість моди в тому, що вона не змінюється при зміні крайніх членів ряду, тобто має певну стійкість до варіації.
називається варіанта, якій відповідає найбільша частість. Особливість моди в тому, що вона не змінюється при зміні крайніх членів ряду, тобто має певну стійкість до варіації.
Отже, для дискретного статистичного ряду
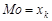 , якщо
, якщо 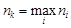 ,
,
а для інтервального статистичного ряду
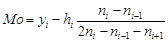 , (28.4)
, (28.4)
де 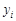 – початок інтервалу з найбільшою частотою,
– початок інтервалу з найбільшою частотою, 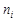 – частота
– частота 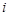 -го інтервалу.
-го інтервалу.
Емпіричною (вибірковою) медіаною 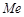 називають середню за розташуванням варіанту дискретного варіаційного ряду, якщо кількість варіант – непарна, і середнім арифметичним двох середніх за розташуванням варіант, якщо кількість варіант – парна. Тобто реалізацію медіани обчислюють так:
називають середню за розташуванням варіанту дискретного варіаційного ряду, якщо кількість варіант – непарна, і середнім арифметичним двох середніх за розташуванням варіант, якщо кількість варіант – парна. Тобто реалізацію медіани обчислюють так:
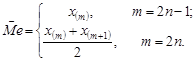
Для інтервальних статистичних рядів
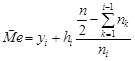 , (28.5)
, (28.5)
де 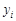 – початок медіанного інтервалу, тобто такого, якому відповідає перша з частот, що перевищує половину всіх спостережень,
– початок медіанного інтервалу, тобто такого, якому відповідає перша з частот, що перевищує половину всіх спостережень, 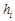 – довжина інтервалу,
– довжина інтервалу, 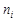 – частота медіанного інтервалу.
– частота медіанного інтервалу.
Приклад 28.1. Обчислити реалізації вибіркового середнього, вибіркової дисперсії, емпіричну моду та медіану за інтервальним статистичним рядом
Таблиця 28.1.
| Інтер. | 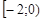
| 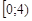
| 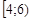
| 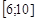
|
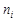
|
Розв’язання. Реалізацію вибіркового середнього для інтервального статистичного ряду обчислюємо за формулою (28.1)
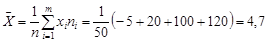 .
.
Реалізацію вибіркової дисперсії знайдемо за формулою (28.3)
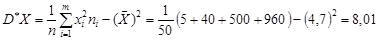 .
.
Моду обчислимо за формулою (28.4)
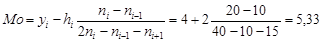 .
.
Відповідно медіану за формулою (28.5)
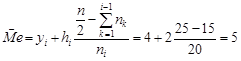 .
.
Емпіричним (вибірковим) коефіцієнтом асиметрії називають статистику 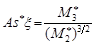 , а емпіричним (вибірковим) ексцесом –
, а емпіричним (вибірковим) ексцесом – 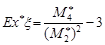 .
.
Дата добавления: 2017-05-18; просмотров: 605;
