Довірчий інтервал для математичного сподівання нормального розподілу

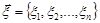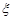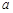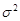Нехай є вибірка з генеральної сукупності випадкової величини , розподіленої за нормальним законом з параметрами та . Поставимо задачу побудови довірчого інтервалу для параметра 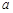з наперед заданою довірчою ймовірністю 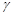. Розділимо задачу на два випадки: 1) дисперсія генеральної сукупності – відома величина; 2) дисперсія генеральної сукупності – невідома.

Отже, нехай відома дисперсія 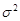випадкової величини 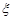. За вибіркою знайдемо вибіркове середнє

.

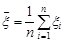Як було вже встановлено (приклад 28.1), вибіркове середнє нормально розподіленої генеральної сукупності є нормально розподіленою випадковою величиною з математичним сподіванням 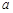та дисперсією .

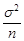Задамо ймовірність 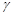та знайдемо величину 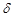, для якої ймовірність події

.

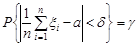Із формул попадання нормально розподіленої випадкової величини в заданий інтервал (13.7) маємо

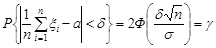. (32.1)

За таблицею значень функції Лапласа знаходимо аргумент 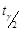, який дорівнює 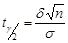. Звідси величина 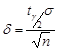. Це значення задає точність шуканого довірчого інтервалу, який в цьому випадку набуває вигляд

.

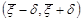Приклад 32.1. Побудувати 96 % довірчий інтервал для оцінки математичного сподівання нормально розподіленої випадкової величини 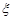, якщо дисперсія 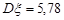, а вибіркове середнє, знайдене за вибіркою, дорівнює 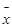= 2.

Розв’язання. За умовою задачі довірча ймовірність 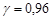. Отже, за формулою (32.1) 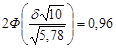. За таблицею значень функції Лапласа знаходимо аргумент, який відповідає числу 0,48:

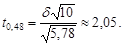
Із цієї рівності отримуємо точність довірчого інтервалу 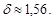Таким чином, довірчий інтервал для математичного сподівання випадкової величини 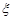буде таким

.

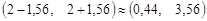Тобто із імовірністю 0,96 можна стверджувати, що точне значення математичного сподівання випадкової величини 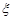знаходиться в саме цьому інтервалі.

Розв’яжемо задачу побудови довірчого інтервалу для математичного сподівання нормально розподіленої випадкової величини 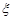у випадку невідомої дисперсії.

За вибіркою знайдемо вибіркове середнє 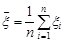та виправлену вибіркову дисперсію 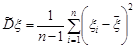. Задамо довірчу ймовірність 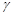. Довірчий інтервал для математичного сподівання випадкової величини 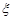також будемо шукати у вигляді

.

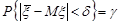Зауважимо, що статистика 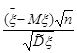, за результатами лекції 23, має розподіл Стьюдента з 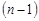ступенями вільності. Отже, за таблицею значень розподілу Стьюдента, при заданій надійності 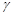і числа 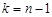, визначимо величину 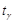таку, що

.

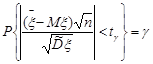Із цієї рівності випливає, що

.

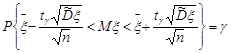Отже, з імовірністю 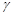можна стверджувати, що вибіркове середнє дає значення невідомого математичного сподівання з точністю 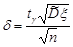, і довірчий інтервал має вигляд

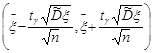. (32.2)

Приклад 32.2. Побудувати 96 % довірчий інтервал для оцінки математичного сподівання 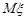нормально розподіленої випадкової величини 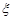, якщо виправлена вибіркова дисперсія 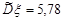, а вибіркове середнє, знайдене за вибіркою, дорівнює 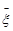= 2.

Розв’язання. На відміну від прикладу 32.1 дисперсія випадкової величини 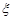невідома, величина 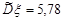є тільки точковою оцінкою дисперсії. За таблицею значень розподілу Стьюдента по 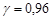та 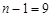знаходимо 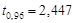. Отже, точність 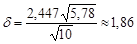. Таким чином, за формулою (32.2) знаходимо довірчий інтервал для математичного сподівання

.

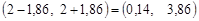Результат цієї задачі означає, що з імовірністю 0,96 довірчий інтервал 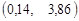накриє невідоме математичне сподівання, а вибіркове середнє 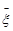= 2 визначає значення 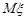з точністю 1,86.

Цей інтервал вийшов ширшим в порівнянні з інтервалом прикладу 32.1. Це пов’язано з тим, що міра невизначеності при оцінці математичного сподівання 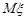більша, оскільки дисперсія 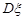є невідомою величиною.

Зауважимо, що при збільшенні обсягу вибірки розподіл Стьюдента зближується з нормальним розподілом, тому при 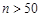величину 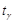можна визначати з таблиці значень функції Лапласа.