Довірчий інтервал для ймовірності появи події при великому обсязі вибірки
За точкову оцінку ймовірності 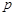 появи події
появи події 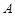 в схемі Бернуллі беруть частість
в схемі Бернуллі беруть частість 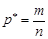 , де
, де 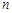 – загальна кількість незалежних випробувань,
– загальна кількість незалежних випробувань, 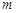 – кількість появ події
– кількість появ події 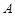 в цих випробуваннях. Задамо довірчу ймовірність
в цих випробуваннях. Задамо довірчу ймовірність 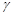 і знайдемо такі величини
і знайдемо такі величини 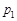 та
та 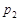 , щоб виконувалось співвідношення
, щоб виконувалось співвідношення
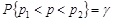 .
.
Інтервал 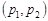 буде шуканим довірчим інтервалом, який відповідає надійності
буде шуканим довірчим інтервалом, який відповідає надійності 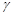 .
.
Розглянемо випадок, коли кількість випробувань у схемі Бернуллі достатньо велике, наприклад, 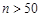 . Крім того, виконуються умови
. Крім того, виконуються умови 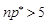 та
та 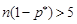 . При виконанні всіх умов розподіл випадкової величини
. При виконанні всіх умов розподіл випадкової величини 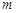 в силу граничної теореми Муавра-Лапласа близький до нормального розподілу
в силу граничної теореми Муавра-Лапласа близький до нормального розподілу 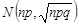 , а випадкова величина
, а випадкова величина 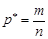 має наближено нормальний розподіл
має наближено нормальний розподіл 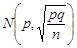 . Таким чином, статистика
. Таким чином, статистика
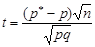
має наближено стандартний нормальний розподіл 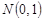 .
.
Користуючись таблицею значень функції Лапласа, для заданої довірчої ймовірності 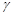 знайдемо таке число
знайдемо таке число 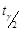 , при якому
, при якому
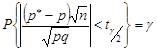 . (32.5)
. (32.5)
Розв’яжемо нерівність, що стоїть у дужках виразу (32.5).
Для цього піднесемо її до квадрату, в результаті отримаємо
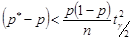 ;
;
піднесемо 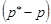 до квадрату та перенесемо всі члени нерівності вліво, будемо мати
до квадрату та перенесемо всі члени нерівності вліво, будемо мати
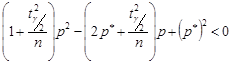 . (32.6)
. (32.6)
Розв’язуючи останню квадратну нерівність, маємо 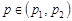 , де
, де
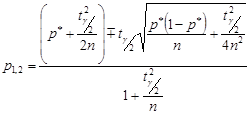 . (32.7)
. (32.7)
Цей результат має геометричну інтерпретацію. Розглянемо Декартові систему координат, по осі абсцис якої відкладаємо частість 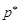 , а по осі ординат – імовірність
, а по осі ординат – імовірність 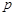 . Точки з координатами
. Точки з координатами 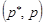 , які задовольняють нерівності (32.6), знаходяться всередині еліпса (рис. 32.2).
, які задовольняють нерівності (32.6), знаходяться всередині еліпса (рис. 32.2).
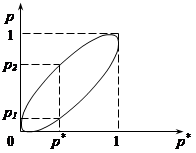 |
Рис. 32.2.
Для того, щоб побудувати інтервальну оцінку ймовірності 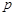 при відомій частості
при відомій частості 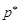 , треба розглянути множину точок всередині еліпса з абсцисою, що дорівнює
, треба розглянути множину точок всередині еліпса з абсцисою, що дорівнює 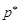 . Цей інтервал і буде шуканим довірчим інтервалом
. Цей інтервал і буде шуканим довірчим інтервалом 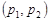 .
.
Якщо обсяг вибірки 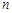 значно більше 100, то величиною
значно більше 100, то величиною 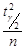 у виразі (32.7) можна знехтувати. Тоді границі довірчого інтервалу набувають наближених виразів
у виразі (32.7) можна знехтувати. Тоді границі довірчого інтервалу набувають наближених виразів
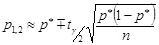 .
.
Приклад 33.1. Подія 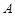 в серії з
в серії з 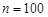 незалежних випробуваннях відбулася
незалежних випробуваннях відбулася 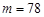 разів. Побудувати довірчий інтервал для ймовірності
разів. Побудувати довірчий інтервал для ймовірності 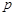 появи події
появи події 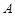 з надійністю
з надійністю 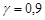 .
.
Розв’язання. За умовою задачі маємо таку точкову оцінку ймовірності 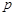
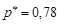 .
.
Оскільки 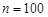 , то границі довірчого інтервалу знайдемо за формулами (32.7), при цьому по
, то границі довірчого інтервалу знайдемо за формулами (32.7), при цьому по 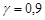 , за таблицею значень функції Лапласа, знайдемо
, за таблицею значень функції Лапласа, знайдемо 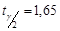 .
.
Отже,
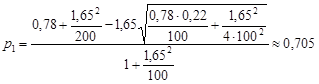 .
.
Відповідно
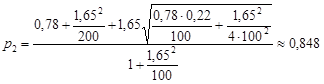 .
.
Отже, з надійністю 0,9 інтервал 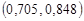 накриє ймовірність
накриє ймовірність 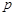 появи події
появи події 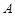 .
.
Дата добавления: 2017-05-18; просмотров: 705;
