Довірчий інтервал для дисперсії та стандартного відхилення нормального розподілу
Нехай 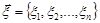 є вибірка з генеральної сукупності випадкової величини
є вибірка з генеральної сукупності випадкової величини 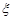 , розподіленої за нормальним законом з параметрами
, розподіленої за нормальним законом з параметрами 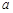 та
та 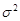 . Поставимо задачу побудови довірчого інтервалу для параметра
. Поставимо задачу побудови довірчого інтервалу для параметра 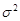 з наперед заданою довірчою ймовірністю
з наперед заданою довірчою ймовірністю 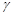 . Як відомо, точковою оцінкою дисперсії є вибіркова дисперсія
. Як відомо, точковою оцінкою дисперсії є вибіркова дисперсія 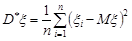 , якщо математичне сподівання відоме, й виправлена вибіркова дисперсія
, якщо математичне сподівання відоме, й виправлена вибіркова дисперсія 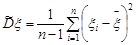 , якщо математичне сподівання випадкової величини
, якщо математичне сподівання випадкової величини 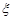 – невідоме. За результатами лекції 23, у випадку відомого математичного сподівання, статистика
– невідоме. За результатами лекції 23, у випадку відомого математичного сподівання, статистика 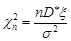 має розподіл хі-квадрат з
має розподіл хі-квадрат з 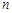 ступенями вільності. Аналогічно, статистика
ступенями вільності. Аналогічно, статистика 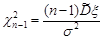 має розподіл хі-квадрат з
має розподіл хі-квадрат з 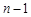 ступенями вільності, якщо математичне сподівання невідоме.
ступенями вільності, якщо математичне сподівання невідоме.
Розглянемо випадок відомого математичного сподівання. При побудові довірчого інтервалу для дисперсії знайдемо 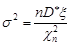 . Крива розподілу величини
. Крива розподілу величини 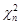 має вигляд (рис. 32.1), тобто не симетрична відносно початку координат.
має вигляд (рис. 32.1), тобто не симетрична відносно початку координат.
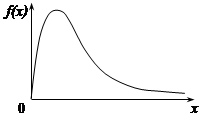 |
Рис. 32.1.
Виберемо інтервал 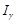 , в який попадає випадкова величина
, в який попадає випадкова величина 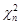 з імовірністю
з імовірністю 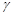 так, щоб імовірності виходу величини
так, щоб імовірності виходу величини 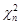 за границі інтервалу вправо та вліво (заштриховані площі на рис. 32.1) були однакові й дорівнювали
за границі інтервалу вправо та вліво (заштриховані площі на рис. 32.1) були однакові й дорівнювали 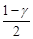 ,
, 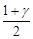 :
:
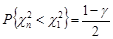 та
та 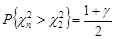 .
.
Для знаходження чисел 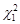 та
та 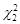 використаємо таблицю значень розподілу хі-квадрат, взяв
використаємо таблицю значень розподілу хі-квадрат, взяв 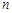 ступенів вільності. Нерівності
ступенів вільності. Нерівності 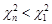 та
та 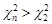 еквівалентні нерівностям
еквівалентні нерівностям 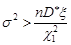 та
та 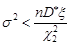 . Отже, шуканий довірчий інтервал для дисперсії нормально розподіленої випадкової величини у випадку відомого математичного сподівання має вигляд
. Отже, шуканий довірчий інтервал для дисперсії нормально розподіленої випадкової величини у випадку відомого математичного сподівання має вигляд
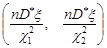 . (32.3)
. (32.3)
Якщо математичне сподівання невідоме, то величини 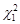 та
та 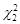 знаходимо також із таблиці розподілу хі-квадрат по значенням
знаходимо також із таблиці розподілу хі-квадрат по значенням 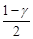 та
та 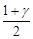 , взявши
, взявши 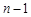 ступінь вільності. Довірчий інтервал при цьому набуває вигляд
ступінь вільності. Довірчий інтервал при цьому набуває вигляд
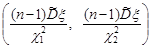 . (32.4)
. (32.4)
Приклад 32.3. Дана вибірка вимірювання дальності до об’єкту в км: 129, 125, 130, 122, 135, 125, 120, 130, 127. Вважаючи, що вимірювання дальності є нормально розподіленою випадковою величиною  , знайти довірчий інтервал для дисперсії цієї величини з надійністю
, знайти довірчий інтервал для дисперсії цієї величини з надійністю 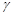 = 0,8.
= 0,8.
Розв’язання. У якості незміщеної оцінки математичного сподівання беремо вибіркове середнє
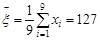 .
.
Незміщеною оцінкою дисперсії в цьому випадку буде виправлена дисперсія
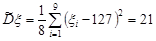 .
.
Оскільки за умовою задачі 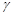 = 0,8, то
= 0,8, то
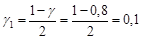 і
і 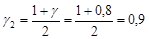 .
.
Кількість ступенів вільності дорівнює 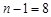 . За таблицею значень розподілу хі-квадрат знаходимо
. За таблицею значень розподілу хі-квадрат знаходимо 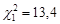 та
та 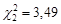 .
.
Отже, за формулою (32.4), границі довірчого інтервалу дорівнюють
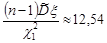 та
та 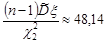 .
.
Таким чином, шуканий довірчий інтервал для дисперсії такий:
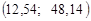 .
.
Дата добавления: 2017-05-18; просмотров: 1024;
