Закон розподілу відношення двох випадкових величин

Закон розподілу добутку двох випадкових величин

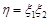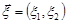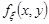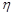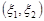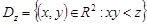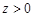Нехай випадкова величина і щільність розподілу випадкового вектора дорівнює . За формулою (21.2) функція розподілу випадкової величини дорівнює ймовірності попадання випадкової точки в область . При ця область зображена на рис.21.1.

Рис.21.1.

Тоді

.

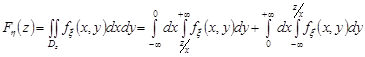Диференціюючи цей вираз по 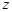, знайдемо щільність розподілу добутку випадкових величин

.

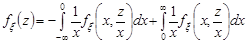Приклад 21.1. Випадкова точка з координатами 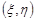має рівномірний розподіл у квадраті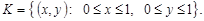

Знайти закон розподілу площі прямокутника із сторонами 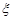та .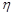

Розв’язання. Площа прямокутника S є випадкова величина, яка дорівнює 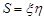, 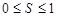. За формулою (21.2) функція розподілу

,

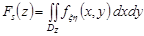де .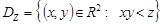

За умовою задачі система випадкових величин 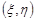має рівномірний розподіл у квадраті К. Це означає, що щільність розподілу ймовірностей випадкового вектора 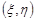має вигляд:

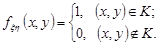
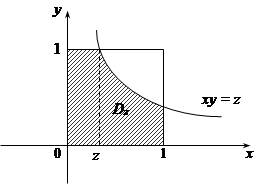При 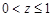область інтегрування 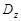має вигляд, що показано на рис. 21.2.

Рис.21.2.

Отже, .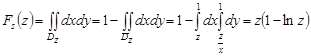

Якщо z>1, то 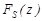=1, при z 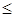0 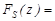0. Остаточно

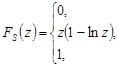
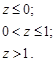
Щільність розподілу площі прямокутника буде дорівнювати

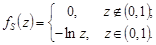
Закон розподілу відношення двох випадкових величин

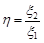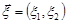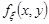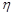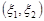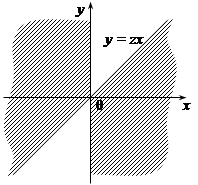
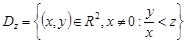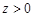Розглянемо закон розподілу відношення двох випадкових величин. Нехай випадкова величина і щільність розподілу випадкового вектора дорівнює . За формулою (21.2) функція розподілу випадкової величини дорівнює ймовірності попадання випадкової точки в область . При ця область зображена на рис.21.3.

Рис.21.3.

Тоді

.

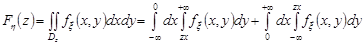Диференціюючи цей вираз по 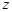, знайдемо щільність розподілу добутку випадкових величин

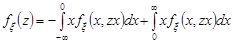. (21.2)

Приклад 21.2. Незалежні випадкові величини 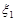та 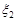розподілені за нормальним законом з параметрами 0 та 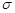. Знайти закон розподілу відношення цих випадкових величин .

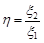Розв’язання. Враховуючи незалежність випадкових величин 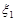, 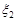та формулу (21.2), маємо

=

.

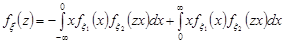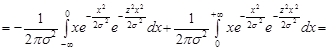
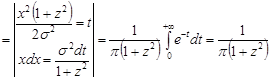Отже, відношення випадкових величин розподілених за законом 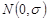має розподіл Коші.