Якщо додаються незалежні випадкові величини, то щільність розподілу суми двох незалежних неперервних випадкових величин знаходиться за формулою
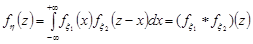 , (21.3)
, (21.3)
тобто згортки законів розподілу доданків. Цей результат узагальнюється на будь-яке число доданків незалежних неперервних випадкових величин:
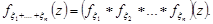
Якщо додаються незалежні випадкові величини, то закон розподілу суми називається композицієюзаконів розподілу доданків.
Закон розподілу випадкової величини називається стійким, якщо композиція законів одного типу дає закон того ж самого типу.
Неважко довести, що закон розподілу суми дискретних незалежних випадкових величин записується у вигляді
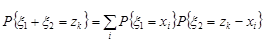 . (21.4)
. (21.4)
 Приклад 21.3. Скласти композицію двох показниковий законів розподілу з параметрами
Приклад 21.3. Скласти композицію двох показниковий законів розподілу з параметрами 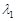 та
та 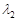 відповідно.
відповідно.
Розв’язання. Щільність розподілу випадкової величини 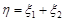 знайдемо за формулою (21.3), враховуючи, що
знайдемо за формулою (21.3), враховуючи, що
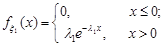 та
та 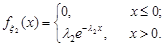
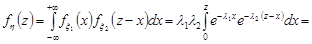
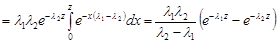 .
.
Вигляд отриманої щільності випадкової величини 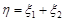 показує, що показниковий розподіл не є стійким. Закон розподілу, що має отриману щільність називається узагальненим законом Ерланга другого порядку.
показує, що показниковий розподіл не є стійким. Закон розподілу, що має отриману щільність називається узагальненим законом Ерланга другого порядку.
Приклад 21.4. Скласти композицію двох рівномірних законів, якщо вони задані відповідно в інтервалах (1, 3) та (2, 5).
Розв’язання. За умовою задачі потрібно знайти закон розподілу суми двох незалежних випадкових величин 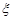 та
та 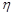 , якщо:
, якщо:
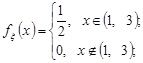
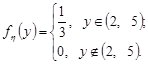
Знаходимо функцію розподілу випадкової величини 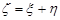 за формулою (21.2). Відомо, що для незалежних випадкових величин виконується рівність:
за формулою (21.2). Відомо, що для незалежних випадкових величин виконується рівність: 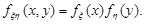 Отже,
Отже, 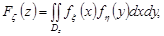 де Dz – область, для якої x+y<z і жодна з функцій
де Dz – область, для якої x+y<z і жодна з функцій 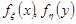 не набуває нульових значень. Область інтегрування буде різною, залежно від того, в якому з проміжків
не набуває нульових значень. Область інтегрування буде різною, залежно від того, в якому з проміжків 
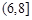 ,
, 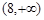 знаходяться значення z. Області інтегрування показані на рисунках:
знаходяться значення z. Області інтегрування показані на рисунках:
1) при z 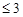 (рис. 21.4)
(рис. 21.4) 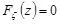 ;
;
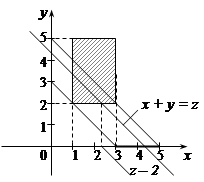
2) при 3<z 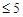 (рис. 21.5)
(рис. 21.5)
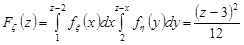 ;
;
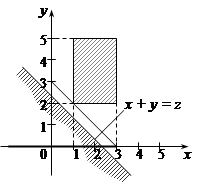
3) при 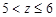 (рис. 21.6)
(рис. 21.6)
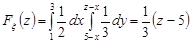 ;
;
4) при 6< z 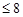 (рис. 21.7)
(рис. 21.7)
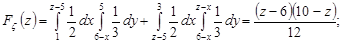
 5) при z >8
5) при z >8 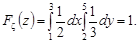

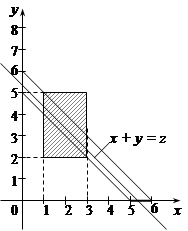 Рис.21.4. Рис.21.5.
Рис.21.4. Рис.21.5.
Рис.21.6. Рис.21.7.
Остаточно маємо:

Щільність розподілу ймовірностей 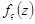 визначимо диференціюванням по z:
визначимо диференціюванням по z:
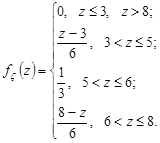
Графічно функції 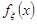 ,
, 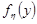 та
та 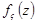 зображені на рис.21.8.
зображені на рис.21.8.
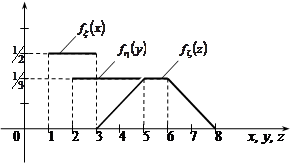 |
Рис.21.8.
Приклад 21.5. Скласти композицію двох законів розподілу Пуассона з параметрами 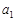 та
та 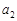 відповідно.
відповідно.
Розв’язання. Нехай випадкові величини 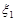 та
та 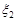 розподілені за законом Пуассона з параметрами
розподілені за законом Пуассона з параметрами 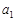 та
та 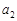 , тоді за формулою (21.4)
, тоді за формулою (21.4)
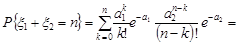
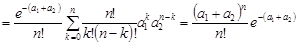 .
.
Отже, закон Пуассона є прикладом стійкого закону розподілу.
21.5. Числові характеристики функцій кількох випадкових аргументів
Питання про находження числових характеристик функцій кількох випадкових аргументів розв’язується аналогічно тому, як знаходились числові характеристики функції одного випадкового аргументу.
Якщо випадкова величина 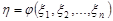 , де випадковий вектор
, де випадковий вектор 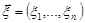 має щільність розподілу ймовірностей
має щільність розподілу ймовірностей 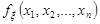 , то числові характеристики випадкової величини
, то числові характеристики випадкової величини 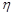 знаходимо за формулами
знаходимо за формулами
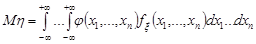 ;
;
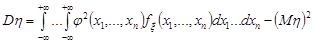 .
.
У випадку 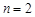 ці формули набувають вигляду
ці формули набувають вигляду
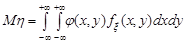 ; (21.5)
; (21.5)
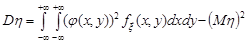 . (21.6)
. (21.6)
Аналогічні формули справедливі для функцій від дискретно розподілених випадкових величин:
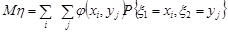 ;
;
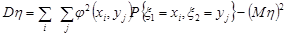 .
.
Отже, для знаходження числових характеристик функцій кількох випадкових аргументів також необов’язково знаходити закон розподілу функції.
Приклад 21.6. Індикатором кругового огляду навігаційної станції є коло з радіусом R. Внаслідок перешкод може з’явитися пляма в будь-якій точці цього кола. Знайти математичне сподівання та дисперсію відстані центра плями до центра кола.
Розв’язання. Випадкова відстань r від центра кола до плями записується через координати  випадкової точки так:
випадкової точки так:  .
.
Система випадкових величин  має рівномірний розподіл. Отже,
має рівномірний розподіл. Отже,

За формулою (21.5) обчислюємо:
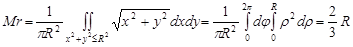 .
.
Дисперсію r знайдемо за формулою (21.6):
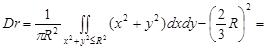
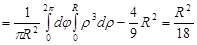 .
.
Наведені формули дають можливість строго довести всі властивості математичного сподівання та дисперсії випадкової величини. Доведемо деякі з них.
1. Математичне сподівання суми випадкових величин дорівнює сумі математичних сподівань доданків: 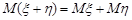 .
.
Доведення. Нехай 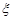 та
та 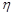 – неперервні випадкові величини з сумісною щільністю розподілу
– неперервні випадкові величини з сумісною щільністю розподілу 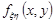 . За формулою (21.5) маємо
. За формулою (21.5) маємо
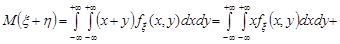
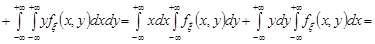
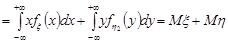 .
.
2. Математичне сподівання добутку незалежних випадкових величин дорівнює добутку математичних сподівань: 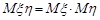 .
.
Доведення. Нехай 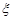 та
та 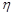 – незалежні неперервні випадкові величини з сумісною щільністю розподілу
– незалежні неперервні випадкові величини з сумісною щільністю розподілу 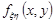 , тоді
, тоді 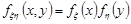 . За формулою (21.5) маємо
. За формулою (21.5) маємо
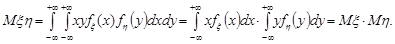
Доведіть всі інші властивості математичного сподівання та дисперсії самостійно.
Дата добавления: 2017-02-20; просмотров: 1166;
