Первинна обробка статистичних даних
Нехай маємо реалізацію вибірки 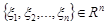 з деякої генеральної сукупності
з деякої генеральної сукупності  . Числа
. Числа 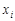 ,
, 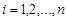 , які утворюють реалізацію вибірки, є спостереженими значеннями випадкової величини
, які утворюють реалізацію вибірки, є спостереженими значеннями випадкової величини 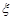 (неперервної чи дискретної). Як правило ці данні представляють собою множину розташованих у будь-якому порядку чисел. Для вивчення закономірностей випадкової величини
(неперервної чи дискретної). Як правило ці данні представляють собою множину розташованих у будь-якому порядку чисел. Для вивчення закономірностей випадкової величини 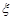 , якщо такі є, дослідні данні треба обробити.
, якщо такі є, дослідні данні треба обробити.
Означення 27.3. Операція, яка полягає в тому, що результати спостережень випадкової величини 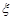 розташовують у порядку не спадання, називається ранжируванням дослідних даних.
розташовують у порядку не спадання, називається ранжируванням дослідних даних.
Покажемо, як це робиться на прикладі.
Приклад 27.4. На телефонній станції проводились спостереження за випадковою величиною 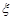 – неправильних з’єднань за хвилину. Спостереження протягом години дали такі результати: 3, 1, 3, 1, 4, 2, 2, 4, 0, 3, 0, 2, 2, 0, 2, 1, 4, 3, 3, 1, 4, 2, 2, 1, 1, 2, 1, 0, 3, 4, 1, 3, 2, 7, 2, 0, 0, 1, 3, 3, 1, 2, 4, 2, 0, 2, 3, 1, 2, 5, 1, 1, 0, 1, 1, 2, 2, 1, 1, 5. Провести первинну статистичну обробку цього статистичного матеріалу.
– неправильних з’єднань за хвилину. Спостереження протягом години дали такі результати: 3, 1, 3, 1, 4, 2, 2, 4, 0, 3, 0, 2, 2, 0, 2, 1, 4, 3, 3, 1, 4, 2, 2, 1, 1, 2, 1, 0, 3, 4, 1, 3, 2, 7, 2, 0, 0, 1, 3, 3, 1, 2, 4, 2, 0, 2, 3, 1, 2, 5, 1, 1, 0, 1, 1, 2, 2, 1, 1, 5. Провести первинну статистичну обробку цього статистичного матеріалу.
Розв’язання. За умовою задачі очевидно, що випадкова величина 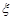 є дискретною випадковою величиною. Обсяг вибірки дорівнює
є дискретною випадковою величиною. Обсяг вибірки дорівнює 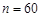 . Якщо розташувати всі числа в порядку не спадання, то отримаємо ранжируванний ряд, в якому є сім різних значень випадкової величини
. Якщо розташувати всі числа в порядку не спадання, то отримаємо ранжируванний ряд, в якому є сім різних значень випадкової величини 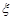 : 0, 1, 2, 3, 4, 5, 7. Значення випадкової величини, яке відповідає окремій групі згрупованого ряду спостережень, називається варіантом, а зміна цього значення – варіюванням. Надалі будемо варіанти позначати малою буквою
: 0, 1, 2, 3, 4, 5, 7. Значення випадкової величини, яке відповідає окремій групі згрупованого ряду спостережень, називається варіантом, а зміна цього значення – варіюванням. Надалі будемо варіанти позначати малою буквою 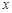 . Для кожної групи згрупованого ряду можна знайти число, що показує, скільки разів зустрічається відповідний варіант у спостережених даних. Ці числа називають частотою варіанта. Надалі будемо їх позначати
. Для кожної групи згрупованого ряду можна знайти число, що показує, скільки разів зустрічається відповідний варіант у спостережених даних. Ці числа називають частотою варіанта. Надалі будемо їх позначати 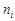 .
.
Означення 27.4. Відношення частот 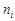 до обсягу вибірки
до обсягу вибірки 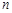 називається частістю або відносними частотами, тобто частості дорівнюють
називається частістю або відносними частотами, тобто частості дорівнюють 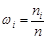 .
.
Зрозуміло, що 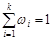 . Неважко помітити, що частість
. Неважко помітити, що частість 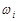 є статистичною ймовірністю появи варіанта
є статистичною ймовірністю появи варіанта 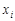 .
.
Знайшовши частоти та частості кожного варіанта нашого прикладу, представимо всі спостереження у вигляді табл. 27.1, яка називається дискретним варіаційним рядом, який строго означимо пізніше.
Таблиця 27.1.
| |||||||
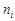
| |||||||
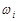
| 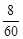
| 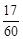
| 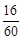
| 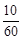
| 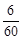
| 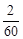
| 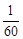
|
Отже, первинна обробка статистичних даних закінчено.
Означення 27.5. Дискретним варіаційним рядом розподілу називається ранжируванна сукупність варіантів 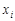 із відповідними їм частотами та частостями.
із відповідними їм частотами та частостями.
Якщо випадкова величина 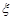 неперервна, то ранжирування та групування спостережень випадкової величини часто не дозволяє виявити характерні риси варіювання її значень. Це пояснюється тим, що окремі значення випадкової величини могуть як завгодно мало відрізнятися одне від одного і тому в сукупності спостережень однакові значення випадкової величини можуть зустрічатися рідко, а частоти варіантів мало відрізнятися. Недоцільно також будувати дискретний варіаційний ряд для дискретної випадкової величини, якщо кількість її можливих значень велика. У подібних випадках будують інтервальний варіаційний ряд розподілу.
неперервна, то ранжирування та групування спостережень випадкової величини часто не дозволяє виявити характерні риси варіювання її значень. Це пояснюється тим, що окремі значення випадкової величини могуть як завгодно мало відрізнятися одне від одного і тому в сукупності спостережень однакові значення випадкової величини можуть зустрічатися рідко, а частоти варіантів мало відрізнятися. Недоцільно також будувати дискретний варіаційний ряд для дискретної випадкової величини, якщо кількість її можливих значень велика. У подібних випадках будують інтервальний варіаційний ряд розподілу.
Означення 27.6. Інтервальним варіаційним рядом розподілу називається упорядкована сукупність інтервалів варіювання значень випадкової величини 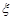 з відповідними частотами та частостями попадань у кожний із цих інтервалів значень.
з відповідними частотами та частостями попадань у кожний із цих інтервалів значень.
Для побудови інтервального варіаційного ряду вибірки, перш за все, знаходять розмах вибірки, тобто різницю між найбільшим і найменшим спостереженням: 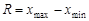 . Далі необхідно вибрати певну кількість інтервалів
. Далі необхідно вибрати певну кількість інтервалів 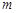 , на які слід поділити розмах вибірки. Кількість інтервалів
, на які слід поділити розмах вибірки. Кількість інтервалів 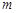 не слід брати великим, оскільки робота з вибіркою буде громіздкою. Але кількість інтервалів не може бути малим, оскільки можна загубити особливість розподілу випадкової величини. Згідно формулі Стерджеса рекомендована кількість інтервалів дорівнює
не слід брати великим, оскільки робота з вибіркою буде громіздкою. Але кількість інтервалів не може бути малим, оскільки можна загубити особливість розподілу випадкової величини. Згідно формулі Стерджеса рекомендована кількість інтервалів дорівнює 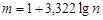 , де
, де 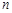 – обсяг вибірки. Отже, величина інтервалів буде дорівнювати
– обсяг вибірки. Отже, величина інтервалів буде дорівнювати
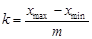 .
.
Після вибору частинних інтервалів, визначають частоти – кількість елементів вибірки 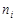 , які потрапили у
, які потрапили у 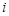 -й інтервал. Якщо елемент лежить на межі інтервалів, то його відносять, наприклад, до правого інтервалу. Поряд із частотами та частостями одночасно обчислюють накопичені частоти
-й інтервал. Якщо елемент лежить на межі інтервалів, то його відносять, наприклад, до правого інтервалу. Поряд із частотами та частостями одночасно обчислюють накопичені частоти 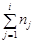 , та накопичені частості
, та накопичені частості 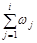 . Отримані результати заносять у таблицю.
. Отримані результати заносять у таблицю.
Приклад 27.5. Нехай задана вибірка з 50 спостережень випадкової величини 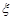 (табл. 27.2):
(табл. 27.2):
Таблиця 27.2.
| 40.67 | 56.6 | 36.6 | 37.34 | 35.19 | 34.00 | 38.31 | 30.74 | 33.99 | 31.81 |
| 34.51 | 26.7 | 48.2 | 25.22 | 18.52 | 27.40 | 28.64 | 21.97 | 20.27 | 23.06 |
| 22.65 | 37.5 | 16.5 | 32.05 | 33.47 | 41.02 | 32.63 | 34.71 | 16.04 | 44.10 |
| 22.27 | 54.8 | 37.9 | 43.21 | 21.73 | 24.15 | 29.81 | 12.95 | 49.87 | 23.76 |
| 14.47 | 35.3 | 20.2 | 20.55 | 25.14 | 26.81 | 31.50 | 42.77 | 25.72 | 32.39 |
Подати вибірку у вигляді інтервального варіаційного ряду.
Розв’язання. Розмах вибірки 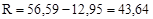 . За формулою Стереджеса треба взяти 7 інтервалів групування. Довжина інтервалу групування
. За формулою Стереджеса треба взяти 7 інтервалів групування. Довжина інтервалу групування 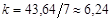 . Для зручності візьмемо
. Для зручності візьмемо 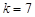 , а перший інтервал
, а перший інтервал  . Підрахуємо середини інтервалів одночасно з відповідними частотами, відносними частотами і накопиченими частотами, які будуть потрібні надалі. Отримані результати зведемо у таблицю 27.3.
. Підрахуємо середини інтервалів одночасно з відповідними частотами, відносними частотами і накопиченими частотами, які будуть потрібні надалі. Отримані результати зведемо у таблицю 27.3.
Таблиця 27.3.
| Номер інтервалу, i | Межі інтервалу | Середина інтервалу, xi | Частота, ni | Накопичена частота | Відносна частота, ni/n | Накопичена відносна частота | |
| нижня | верхня | ||||||
| 15.5 | 0.1 | 0.1 | |||||
| 22.5 | 0.26 | 0.36 | |||||
| 29.5 | 0.22 | 0.58 | |||||
| 36.5 | 0.24 | 0.82 | |||||
| 43.5 | 0.1 | 0.92 | |||||
| 50.5 | 0.04 | 0.96 | |||||
| 57.5 | 0.04 |
Дата добавления: 2017-05-18; просмотров: 1166;
