Математические методы в исследованиях

Решение практических задач математическими методамиосуществляется путем реализации этапов следующего алгоритма:

- разработка математической модели;

- выбор метода проведения исследования математической модели;

- анализ полученного математического результата.

Математическая модель− система формул, функций, уравнений, средствами которых описывается то или иное явление, процесс, объект в целом. При разработке модели нужно учитывать все реально существующие связи факторов и параметров, хотя при этом нельзя забывать о возможности последующего решения математической модели. Следует прибегать к каким-либо упрощениям, допущениям, аппроксимациям. Для модели физического процесса необходимо определить:

1) область или границы применения модели;

2) физические ограничения;

3) требуемую точность результатов;

4) константы и переменные процесса;

5) управляемые переменные;

6) неуправляемые переменные.

В теоретических исследованиях следует выделить детерминированныеи вероятностные математические методы, которые могутбыть статическимии динамическими.

Детерминированные статическиеметоды опираются на алгебру и дифференциальные уравнения с независимыми от времени аргументами.

Детерминированные динамическиеметоды опираются на алгебру, интегральные уравнения, дифференциальные уравнения с частными производными, теорию автоматического управления.

Вероятностные статическиеметоды опираются на алгебру, теорию вероятностей и теорию информации, а вероятностные динамические– на дифференциальные уравнения, теорию случайных процессов и теорию автоматов.

Кроме этого, в математических методах исследования широко применяются численные методы решениязадач. Например:

- в решении нелинейных уравнений – этометод деления отрезка пополам, хорд, касательных, простых итераций;

- в решении интегралов – метод прямоугольников, трапеций, парабол (Симпсона);

- в решении дифференциальных уравнений – методлевых, правых и средних разностей, метод Эйлера и др.;

- в решении оптимизационных задач – метод перебора, «золотого» сечения, покоординатного спуска, градиентного спуска, линейного программирования;

- в решении аппроксимационных задач – логарифмические, степенные, показательные ряды и многочлены.

Рассмотрим практический пример по теме научного исследования «Обеспечения точности цилиндрических зубчатых изделий на операциях электроэрозионного вырезания, выполняемых на станках с ЧПУ».

Сформулируем задачу теоретического исследования: «Установить функциональную взаимосвязь конструктивно-технологических

факторов процесса электроэрозионного вырезания цилиндрических

эвольвентных зубчатых изделий с одним из показателей точности

взаимного расположения боковых поверхностей зубьев зубчатого изделия – отклонением шага зацепления f_pbr и определить условия

обеспечения заданной точности по этому параметру».

Реализуем решение задачи теоретического исследования (укрупненно).

Установлено, что математическая модель, связывающая f_pbr с

конструктивно-технологическими факторами, имеет следующий вид в

кодированных показателях:

ŷ = F (X1; X2; X3; X4; X5; X6; X7; X8), (1)

где ŷ – наибольшее отклонение шага зацепления f_pbr ^max, мкм; X1 – мо-

дуль зубчатого изделия m, мм; X2 – число зубьев зубчатого изделия

z; X3 – погрешность линейных перемещений инструмента (калибро-

ванная проволока) по оси x Δ ₂ ^х , мкм; X4 – погрешность линейных перемещений инструмента по оси Y Δ₂^y, мкм; X5 – дискретность системы ЧПУ станка Д, мм; X6 – число формообразующих точек траектории торцового эвольвентного профиля зуба зубчатого изделия N1; X7– вариант задания координат точек траектории; X8 – тип интерполятора системы ЧПУ станка.

Факторы X1, X2, X6 – варьируемые, X3, X4, X5– принимаются по модели станка, X7, X8 – постоянные.

С учетом установленных ограничений и условий:

m = 1,25 … 10 мм ; z = 20 … 80; N1 = 7 … 30; координаты зада-

ют в абсолютных величинах; интерполятор – линейный. Реализовав

методику проведения полнофакторного эксперимента, для условий

обработки на вырезном станке СВЭИ-7 при Δ ₂ ^х = 5 мкм, Δ ₂ ^y= 5 мкм

и Д = 1 мкм, получили зависимость

f_pbr ^max = −2,483 + 9,944 · m + 4,509 · 10^-2 · z +

+3,780 · 10^-2 ∙ N1 – 3,947 · 10^-2 · m · z – 0,324 · m · N1 −

−3,095 · 10^-4 · z · N1 + 1,850 · 10^-3 · z · m · N1. (2)

По зависимости (модели) (2) можно рассчитать f_pbr ^max

при различных m, z и N1, учитывая заданную степень точности зубчатого изделия, и построить графики, опираясь на которые, определить условия обеспечения заданной точности по анализируемому параметру.

Например, для зубчатого изделия восьмой степени точности при z = 40 и m= 1,25 … 10 мм получаем графики, показанные на рис. 1.

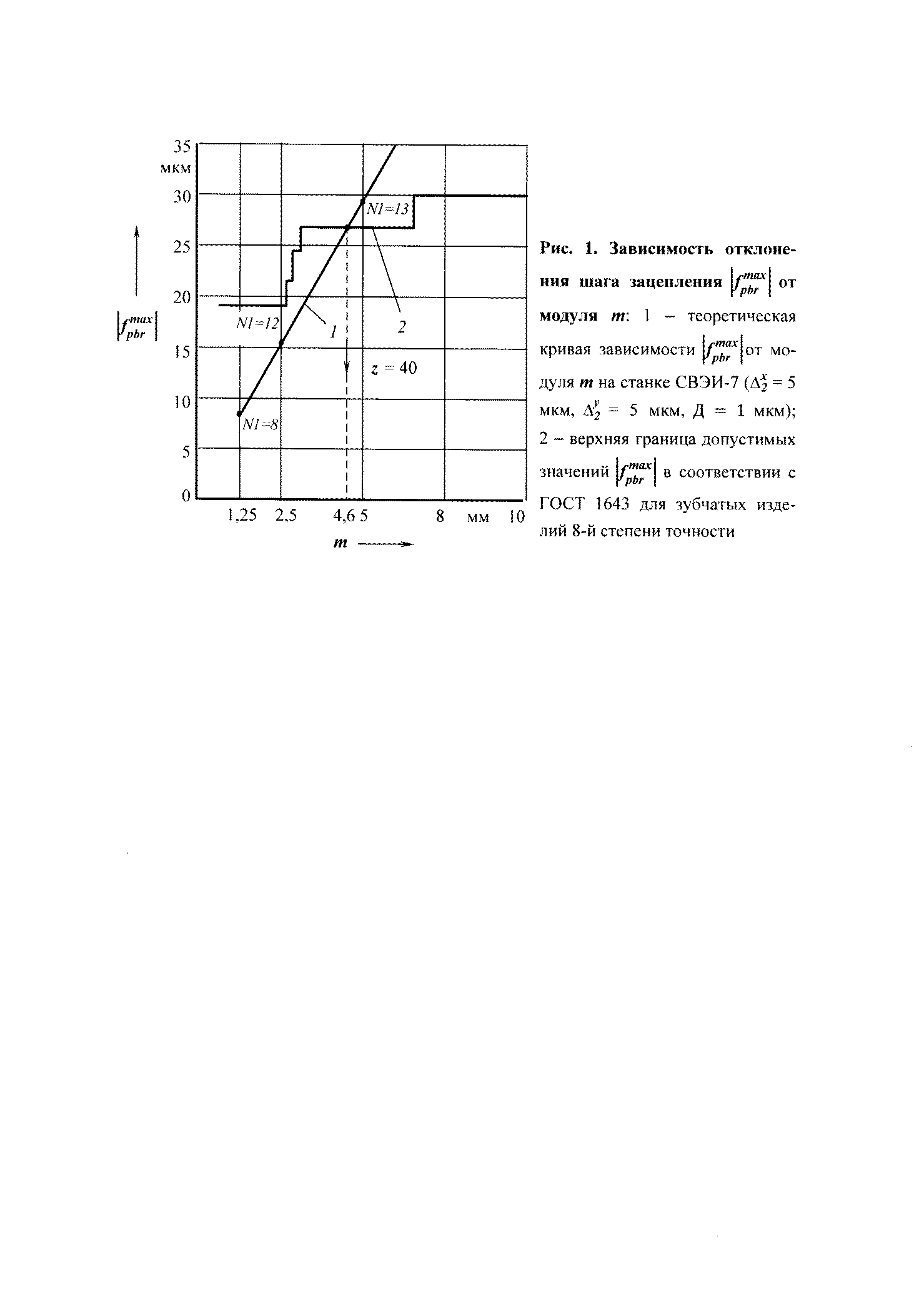
Анализ графиков, показанных на рис. 1, привел к выводу о том,

что рекомендуемыми для обработки на станке СВЭИ-7, с учетом

обеспечения восьмой степени точности, будут зубчатые изделия с

числом зубьев z = 40 и модулем m от 1,25 до 4,6 мм. При дальнейшем увеличении m заданная точность параметра f_pbr ^max обеспечиваться не будет (действительные значения отклонения шага зацепления выходят за границу допустимых).