Непараметрические методы оценки связи
Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили названиепараметрических методов.
Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили названиенепараметрических.
Если изучается взаимосвязь двух качественных признаков, то используют комбинационное распределение единиц совокупности в форме так называемых таблиц взаимной сопряженности.
Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.
| Занятия родителей | Число детей, занятых в | Всего | |||
| Промышлен- ности и стро- ительстве | сельском хозяйстве | сфере обслужи- вания | сфере интел- лектуального труда | ||
| 1. Промышленность и строительство 2. Сельское хозяйство 3. Сфера обслуживания 4. Сфера интеллектульного труда | 40 34 16 24 | 5 29 6 5 | 7 13 15 9 | 39 12 19 72 | 91 88 56 110 |
| Всего |
Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 («Промышленность и строительство») заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т.д.
Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т.д.
Однако важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях. Для этой цели исчисляют, например, коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):
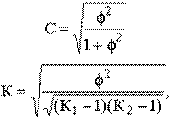
где f2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
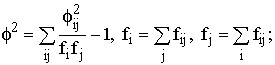
К1 и К2 – число групп по каждому из признаков. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в обычных для этих показателей пределах от 0 до 1.
В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.
При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.
Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (r) и Кендэлла (t). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.
Вопросы для самоконтроля
1.В чем заключаются основные задачи изучения и измерения связи между явлениями?
2.Какая связь называется функциональной и в каких областях науки она наиболее широко распространена?
3.Какая связь называется корреляционной и в чем ее сущность?
4.Какие бывают виды связи по направлению?
5.Что такое парная связь?
6.Что представляет собой прямолинейная и криволинейная связь и как она выражается математически?
7.Какие методы применяются статистикой для установления измерения связи между явлениями?
8.Как измеряют тесноту связи?
9.Для чего при установлении связи между явлениями широко применяют аналитические группировки?
10. Какие задачи решает дисперсионный анализ?
11. Как исчисляется корреляционное отношение, что оно характеризует и в каких пределах колеблется его абсолютное значение?
12. Каковы задачи корреляционного анализа?
13.Что означает определить форму связи между признаками?
14.Что представляет собой корреляционная таблица?
15.Как определяют теоретические значения Y в чем состоит основное условие способа наименьших квадратов?
16. Какое уравнение называется линейным корреляционным уравнением и что характеризуют его параметры?
17. Как определяется достоверность коэффициента регрессии?
18.Что представляет собой линейный коэффициент корреляции.
19.Что характеризует коэффициент детерминации, какова его формула и чем он отличается от корреляционного отношения?
20. Как проводится оценка существенности связи в корреляционном анализе?
21. Какие простейшие методы измерения тесноты связи вы знаете?
22. На чем основан коэффициент корреляции знаков и как он исчисляется?
23. Как определяется коэффициент корреляции рангов?
24. Когда применяется коэффициент ассоциации и порядок его вычисления?
25. В каких случаях применяется коэффициент взаимной сопряженности и порядок его вычисления?
Дата добавления: 2017-04-20; просмотров: 593;
