Эмпирическое корреляционное отношение

Для измерения тесноты связи применяется несколько показателей. При парной связи теснота связи определяется, прежде всего, корреляционным отношением, которое обозначается η. Квадрат корреляционного отношения – это отношение межгрупповой дисперсии результативного признака, которая выражает влияние различий группировочного факторного признака на среднюю величину результативного признака, к общей дисперсии результативного признака, выражающей влияние на него всех причин и условий. Квадрат корреляционного отношения называется коэффициентом детерминации.

ыми явлениями и их признаками: ­­­­­­­­­­­­­________________ или жестко детермини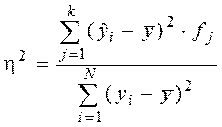

где k- число групп

N – число наблюдений

y_i – исходные значения результативного признака

y_j – средние значения результативного признака для данной группы

y – среднее значение признака

f_j – численность группы

Указанная выше формула применяется при расчете показателя тесноты связи по аналитической группировке. При вычислении корреляционного отношения по уровню связи применяется формула:

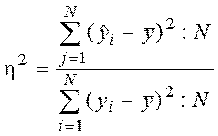
Сумма квадратов в числителе ­– это объясненная связью с фактором х (факторами) дисперсия результативного признака у. Она вычисляется по индивидуальным данным, полученным для каждой единицы совокупности на основе уравнения регрессии.

Если уравнение выбрано неверно или сделана ошибка при расчете его параметров, то сумма квадратов в числителе может оказаться больше чем в знаменателе, и отношение утратит тот смысл, который должно иметь. Чтобы избежать ошибочного результата, лучше вычислять корреляционное отношение по следующей формуле:

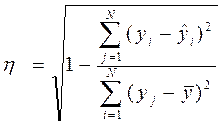
В основе указанной формулы лежит известное правило разложения сумм квадратов отклонений при группировке совокупности:

D_общ = D_межгр+D_{внутригр}

Согласно этому правилу можно вместо межгрупповой (факторной) дисперсии использовать разность:

D_общ –D_{внутригр}

что дает:

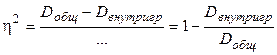
При расчете η не по группировке, а по уравнению корреляционной связи (уравнению регрессии) мы используем формулу. В этом случае правило разложения суммы квадратов отклонений результативного признака записывается как

D_общ= D_кор +D_ост

Важнейшее положение, которое следует теперь усвоить любому, желающему правильно применять метод корреляционно-регрессионого анализа, состоит в интерпретации формул (1.2) и (1.3). Это положение гласит:

Уравнение корреляционной связи измеряет зависимость между вариацией результативного признака и вариацией факторного признака (признаков). Меры тесноты связи измеряют долю вариации результативного признака, которая связанна с вариацией факторного признака (признаков).