Основы выборочного метода
Статистическое исследование может осуществляться по данным несплошного наблюдения, основная цель которого состоит в получении характеристик изучаемой совокупности по обследованной ее части. Одним из наиболее распространенных в статистике методов, применяющих несплошное наблюдение, является выборочный метод.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора.
Значение выборочного метода состоит в том, что при минимальной численности обследуемых единиц проведение исследования осуществляется в более короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.
Преимущества выборочного наблюдения заключаются в существенной экономии различного вида ресурсов, а именно:
• финансовых средств, затрачиваемых на сбор и обработку данных, подготовку и оплату кадров;
• материально-технических ресурсов (канцелярские товары, оргтехника, расходные материалы, транспортное обслуживание и т.п.),
• трудовых ресурсов, привлекаемых к обследованию на всех его этапах;
• времени, затрачиваемого как на получение первичной информации, так и на последующую ее обработку, вплоть до публикации итоговых материалов.
В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов
При этом подлежащая изучению статистическая совокупность, из которой производится отбор части единиц, называется генеральной совокупностью.Отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию, называется выборочной совокупностью или просто выборкой.
В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозначается р), а средняя величина изучаемого варьирующего признака — генеральной средней (обозначается 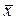 ).
).
Генеральная доля определяется из отношения единиц генеральной совокупности, обладающих изучаемым признаком М, к общей численности единиц генеральной совокупности N:
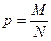
В выборочной совокупности долю изучаемого признака называют выборочной долей (обозначается 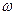 ), а среднюю величину в выборке — выборочной средней (обозначается
), а среднюю величину в выборке — выборочной средней (обозначается 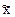 ).
).
Выборочная доля 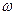 определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:
определяется из отношения единиц, обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:
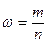
Отбор единиц в выборочную совокупность может быть повторным или бесповторным. При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения. Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется. На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Необходимо отметить, что в выборочную совокупность могут отбираться не только отдельные единицы, но и группы единиц. В первом случае отбор называется индивидуальным, во втором случае - групповым.
Ошибки выборки
Ошибки выборочного наблюдения, которые иначе называют ошибками репрезентативности, возникают вследствие специфики самого метода и именно потому, что обследуется не вся совокупность, а лишь его часть, отобранная в случайном порядке.
Определение средней величины этих ошибок и их возможных границ, а следовательно, определение достоверности данных выборочного наблюдения, является основной задачей теории выборочного исследования.
Ошибка выборки— это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методом отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования.
Теория и практика применения выборочного метода показали, что данные выборочного наблюдения достаточно достоверны, так как выборочный метод базируется на применении закона больших чисел и теории вероятности. Сущность закона больших чисел заключается втом, что чем больше будет взято единиц поднаблюдение, тем точнее средняя выборочная будет воспроизводить среднюю генеральную.
Теория выборочного метода дает формулу, по которой можно вычислить среднюю величину ошибки для выборочной совокупности, отобранной в случайном порядке, т.е. таким образом, что каждая единица генеральной совокупности имела бы равную возможность попасть в это число.
Определение ошибкивыборочной средней:
1). При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:
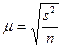 ,
,
где 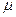 — средняя ошибка выборочной средней;
— средняя ошибка выборочной средней;
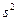 — дисперсия выборочной совокупности;
— дисперсия выборочной совокупности;
n — численность выборки.
2). При бесповторном отборе она рассчитывается по формуле:
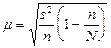 ,
,
где N — численность генеральной совокупности.
Величина средней ошибки выборки зависит прежде всего от показателей колеблемости значений признаков в выборочной совокупности. Степень колеблемости значений признаков определяется средним квадратическим отклонением.
Чем меньше величина среднего квадратического отклонения (следовательно, чем однороднее совокупность), тем меньше величина средней ошибки при той же численности выборки.
Кроме того, величина средней ошибки зависит от численности выборки. Увеличивая или уменьшая объем выборки, можно регулировать величину ошибки. Чем больше единиц будет охвачено выборочным наблюдением, тем меньше будет величина ошибки, так как тем точнее будет представлена генеральная совокупность. Полученная величина ошибки характеризует среднее отклонение средней выборочной от средней генеральной.
Определение ошибки выборочной доли:
1). При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:
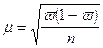 ,
,
где 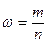 — выборочная доля единиц, обладающих изучаемым признаком;
— выборочная доля единиц, обладающих изучаемым признаком;
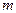 — число единиц, обладающих изучаемым признаком;
— число единиц, обладающих изучаемым признаком;
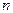 — численность выборки.
— численность выборки.
2). При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:
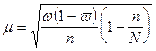
На практике при применении выборочного метода обычно ставится задача определения пределов, за которые не выйдетвеличина конкретной ошибки выборочного наблюдения.
Величина пределов конкретной ошибки зависит от степени вероятности, с которой измеряется ошибка выборки.
Ошибка выборки, исчисленная с заданной степенью вероятности, представляет предельную ошибку выборки.
Предельная ошибка выборки 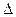 связана со средней ошибкой выборки
связана со средней ошибкой выборки 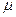 отношением:
отношением:
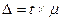 .
.
При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.
Величину вероятности для различных значений t можно определить на основе теоремы Ляпунова. На практике пользуются готовыми таблицами значений этой функции, вычисленных для различных значений t. С увеличением значения t вероятность Р быстро приближается к единице, так что практически обычно ограничиваются значениями t, не превышающими 2—3 единицы:
Р = 0,683 t = 1
Р = 0,954 t = 2
Р = 0,997 t = 3
Уже при значении t, равном 3, вероятность очень близка к единице. Это означает, что если бы из одной и той же генеральной совокупности было произведено большое число случайных выборок одинаковой численности, то в среднем на 1000 выборок приходилось бы 997 таких, в которых отклонение выборочной средней от генеральной не превышало бы 3 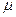 , и только в трех выборках отклонение могло бы выйти за эти пределы.
, и только в трех выборках отклонение могло бы выйти за эти пределы.
Указывая вероятные пределы случайной ошибки выборки, мы тем самым указываем и те пределы, за которые не выйдет характеристика генеральной совокупности, т.е. решаем ту задачу, которая, собственно, и ставится при выборочном наблюдении.
Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:
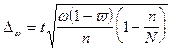 ,
,
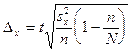 .
.
Предельная ошибка выборки при повторном отборе определяется по формуле:
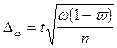 ,
,
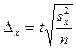 .
.
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:
для средней 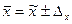
для доли 
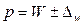
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения. Чем больше объем выборки, тем меньше значения средней и предельной ошибок выборочного наблюдения и, следовательно, тем уже границы генеральной средней и генеральной доли. В то же время необходимо учитывать, что большой объем выборки приводит к удорожанию обследования, увеличению сроков сбора и обработки материалов, требует привлечения дополнительного персонала и соответствующего материально-технического обеспечения. Поэтому при подготовке выборочного наблюдения необходимо определить тот минимально необходимый объем выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности.
Необходимый объем повторной выборки при определении средней величины может быль рассчитан по формуле:
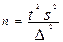
а объем бесповторной выборки:
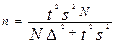
Численность повторной выборки при изучении доли определяется следующим образом:
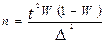
бесповторной выборки:
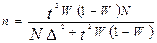
Дата добавления: 2017-04-20; просмотров: 2054;
